The fastest way to take 35 billboards in Moscow
Ideas to do on the weekends, IT is drawn from hundreds of different sources. I, for example, recently saw the competition of the Open School Championship in Economics, which is to photograph the maximum number of Championship billboards . The organizers have kindly provided the addresses. And despite the fact that the prize for an adult does not shine there (this is a school competition), it would nevertheless be extremely interesting to find out in what minimum time such a task can be solved.
3 hours on weekends, 35 billboard addresses in the form of quite controversially injected addresses (for some reason, the UNOM registry fights badly with familiar maps), 1 Jupyter with the second ( sorry ) python and many API of various services ready to work.
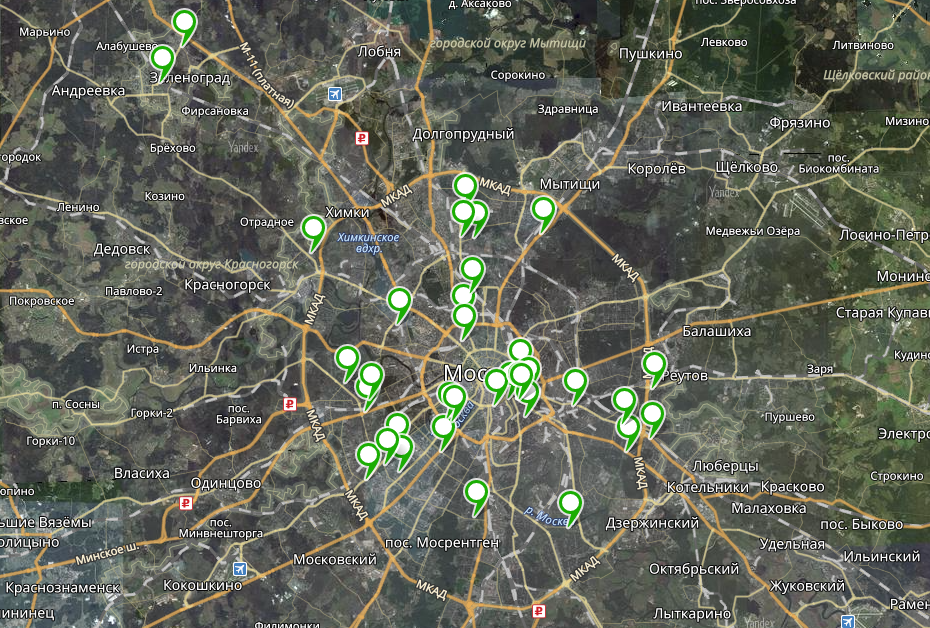
For a start, it would be convenient to present the scale of the disaster on the map. It would be possible to use something automatic, but it’s faster to manually kill 35 addresses in the Yandex.Maps Constructor, he will lead them to the coordinate. The result was a picture of kata , from which it became clear that
')
Actually all the options to continue this route , which is roughly comparable to the number of unique chess positions on the board. So we need to understand a little about the achievements of the national economy in the field of P-NP tasks .
It becomes clear that our task is an example of the classic traveling salesman (TSP) problem . In order to solve it (approximately), we need to build a distance matrix (in our case, time) between each point. To solve this problem, we will use the Google Maps API, namely, the insanely simple and clear googlemaps library. Working with this library is simple and elegant. You can get time between two points on the map so simply:
So, it remains to fill the matrix of 36 × 36 all distances. Note that getting from point A-> B does NOT take as much time as from B-> A, so reducing the work by two times will not work (although the diagonal is of course filled with zeros). It would be possible to just go through the previously created empty matrix and fill it, but I prefer the approach when I first store all the elements of the matrix as a list
Here you can immediately note that I am a big fan of Pandas Dataframes, and with them life becomes better. If you have not heard, be sure to read, you will like it. And, of course, how good it is to write on Python, in which the wonderful function
The final matrix turned out like this:

By the way, here you can immediately explore, and how close are our points at all? In other words, look at the distribution of travel time between all points:
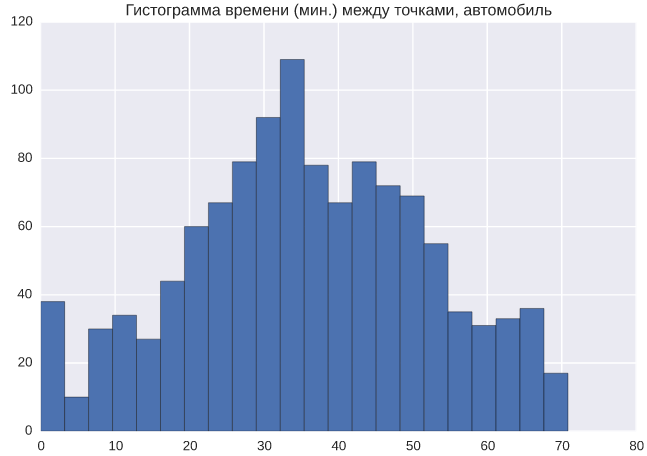
Although in general, everything is quite expected. Many points are very close, the distribution is quite “normal”, all due to the fact that by car you can move in any direction. Looking ahead, here is the same distribution, only for public transport:

A completely different picture: the distribution is much more “stretched” to the right, that is, there are relatively few points between which one can quickly (faster than 40 minutes) move by public transport. And of course, the time spent on transport in general is more (more or less twice).
So, now on the matrix it is necessary to build the best route. I must say that this task has already been studied quite well, for example, there is a very good google library ortools , which allows you to iterate through routes on thousands and tens of thousands of points.
However, in our case there are only a dozen points. There is no need for complex algorithms. You can use the greedy algorithm of double pass, and get the result almost no different from the "canonical".
So, the algorithm will be like this:
1. We initiate the initial and final points.
2. We take two points with the shortest distances from the initiated ones, add them to the route.
3. Postorim until we get the full route.
It is obvious here that the algorithm is very dependent on the selected initial points (and generally on the order of the points), so there is a fairly simple way to avoid local optima: “mix” the points several times and post the work of the greedy algorithm.
I borrowed the software implementation of this algorithm from the library of Dmitry Shinyakov from the library.
The library accepts the
The same can be done using Yandex.Maps, without breaking into two pieces.
I laid out all the code on my github as a jupyter notebook so that I could quickly try to do something similar.
So, in the end, the algorithm gave an estimate of time at 8 o'clock (without traffic jams for 6 hours). At that moment, I wanted to get out of the comfort zone of the cute online, and really take a ride and take a picture of all the billboards. Things are easy: the company was found, and we drove strictly in accordance with the constructed route.
The final journey took only 10 hours. Taking into account the stops and the search for many billboards, it seems to me that the “extra” 25% of the time is fully justified. We managed to drive through all the points in the list, but found only 23 of 35 billboards. At the same time, it is interesting that we found 19 out of 24 billboards of 6x3 format, and only 4 of 11 cityboards. Most likely this is due to the fact that city formats in general are more attractive to advertisers (because they are located closer to the center), and therefore they are removed faster . I do not exclude the banal version that billboards, in principle, did not hang.
As a result, it seems to me, it turned out to be a rather interesting mix of a simple algorithm that simplifies the routine and gives a much better result than a person, and a real use of it on the roads of Moscow. We did not win the children's competition of the Open School Championship in Economics, but it seemed that we found an order of magnitude more billboards than the most active participant.

So what do we have?
3 hours on weekends, 35 billboard addresses in the form of quite controversially injected addresses (for some reason, the UNOM registry fights badly with familiar maps), 1 Jupyter with the second ( sorry ) python and many API of various services ready to work.
For a start, it would be convenient to present the scale of the disaster on the map. It would be possible to use something automatic, but it’s faster to manually kill 35 addresses in the Yandex.Maps Constructor, he will lead them to the coordinate. The result was a picture of kata , from which it became clear that
')
- Three points are located in Zelenograd and Khimki, they will clearly increase the time on the way.
- Few billboards in the city center
- The points are quite chaotic, and manually build a good route connecting them is unlikely to work.
Actually all the options to continue this route , which is roughly comparable to the number of unique chess positions on the board. So we need to understand a little about the achievements of the national economy in the field of P-NP tasks .
Collect time matrix between points
It becomes clear that our task is an example of the classic traveling salesman (TSP) problem . In order to solve it (approximately), we need to build a distance matrix (in our case, time) between each point. To solve this problem, we will use the Google Maps API, namely, the insanely simple and clear googlemaps library. Working with this library is simple and elegant. You can get time between two points on the map so simply:
import googlemaps import datetime gmaps = googlemaps.Client(key='AIxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx') resp = gmaps.directions( origin='55.71802 37.573753', destination='55.73481 37.66521', mode='driving', # 'transit' region='ru', language='en', departure_time=datetime.datetime.now(), ) distance_time = resp[0]['legs'][0]['duration_in_traffic']['value'] # print resp[0]['legs'][0]['duration_in_traffic'] # Out[]: {u'text': u'49 mins', u'value': 2917} So, it remains to fill the matrix of 36 × 36 all distances. Note that getting from point A-> B does NOT take as much time as from B-> A, so reducing the work by two times will not work (although the diagonal is of course filled with zeros). It would be possible to just go through the previously created empty matrix and fill it, but I prefer the approach when I first store all the elements of the matrix as a list
[[x,y,value]] , and then I do .pivot , “ .pivot ” the matrix . distances = [] for origin,destination in permutations(points['lat lng'], 2): resp = gmaps.directions( origin=origin, destination=destination, mode='driving', region='ru', language='en', departure_time=now, ) distance_time = resp[0]['legs'][0]['duration_in_traffic']['value'] # distances.append( [origin,destination,distance_time] ) distances = pd.DataFrame(distances, columns='origin,destination,distance_time'.split(',')) distances_matrix = distances.pivot_table( index='origin', columns='destination', values='distance_time' ).fillna(0) Here you can immediately note that I am a big fan of Pandas Dataframes, and with them life becomes better. If you have not heard, be sure to read, you will like it. And, of course, how good it is to write on Python, in which the wonderful function
itertools.permutations is already ready, which returns all pairs (triples, quadruples, as needed) of the elements of a given list. No crutches!The final matrix turned out like this:

By the way, here you can immediately explore, and how close are our points at all? In other words, look at the distribution of travel time between all points:

Although in general, everything is quite expected. Many points are very close, the distribution is quite “normal”, all due to the fact that by car you can move in any direction. Looking ahead, here is the same distribution, only for public transport:

A completely different picture: the distribution is much more “stretched” to the right, that is, there are relatively few points between which one can quickly (faster than 40 minutes) move by public transport. And of course, the time spent on transport in general is more (more or less twice).
Tsp
So, now on the matrix it is necessary to build the best route. I must say that this task has already been studied quite well, for example, there is a very good google library ortools , which allows you to iterate through routes on thousands and tens of thousands of points.
However, in our case there are only a dozen points. There is no need for complex algorithms. You can use the greedy algorithm of double pass, and get the result almost no different from the "canonical".
So, the algorithm will be like this:
1. We initiate the initial and final points.
2. We take two points with the shortest distances from the initiated ones, add them to the route.
3. Postorim until we get the full route.
It is obvious here that the algorithm is very dependent on the selected initial points (and generally on the order of the points), so there is a fairly simple way to avoid local optima: “mix” the points several times and post the work of the greedy algorithm.
I borrowed the software implementation of this algorithm from the library of Dmitry Shinyakov from the library.
The library accepts the
numpy square matrix as input, and the output produces path : an array of indices of points in the order along the route. Interestingly, Google Maps does not allow you to build routes with more than 23 waypoints, so you cannot build a route on one map. I went to the trick, and with the help of the same googlemaps simply split the route into two and built it. coords_path = distances_matrix.index[path] # # Latitude-longitude pairs start = map(float, coords_path[0].split(' ')) waypoints = map(lambda p: map(float, p.split()), coords_path[1:24]) # 24 end = map(float, coords_path[24].split()) m = gmaps.Map(height='650px') ochDirections = gmaps.directions_layer(start, end, waypoints=waypoints) m.add_layer(ochDirections) start = map(float, coords_path[24].split(' ')) waypoints = map(lambda p: map(float, p.split()), coords_path[25:-1]) end = map(float, coords_path[-1].split()) ochDirections = gmaps.directions_layer(start, end, waypoints=waypoints) m.add_layer(ochDirections) m The same can be done using Yandex.Maps, without breaking into two pieces.
base_yandex = 'https://yandex.ru/maps/213/moscow/?ll=37.519600%2C55.819741&z=10&mode=routes&rtext={rtext}&rtt=mt&rtm=atm' rtext = '~'.join(i.replace(' ', '%2C') for i in coords_path) print base_yandex.format(rtext=rtext) I laid out all the code on my github as a jupyter notebook so that I could quickly try to do something similar.
The result is
So, in the end, the algorithm gave an estimate of time at 8 o'clock (without traffic jams for 6 hours). At that moment, I wanted to get out of the comfort zone of the cute online, and really take a ride and take a picture of all the billboards. Things are easy: the company was found, and we drove strictly in accordance with the constructed route.
The final journey took only 10 hours. Taking into account the stops and the search for many billboards, it seems to me that the “extra” 25% of the time is fully justified. We managed to drive through all the points in the list, but found only 23 of 35 billboards. At the same time, it is interesting that we found 19 out of 24 billboards of 6x3 format, and only 4 of 11 cityboards. Most likely this is due to the fact that city formats in general are more attractive to advertisers (because they are located closer to the center), and therefore they are removed faster . I do not exclude the banal version that billboards, in principle, did not hang.
As a result, it seems to me, it turned out to be a rather interesting mix of a simple algorithm that simplifies the routine and gives a much better result than a person, and a real use of it on the roads of Moscow. We did not win the children's competition of the Open School Championship in Economics, but it seemed that we found an order of magnitude more billboards than the most active participant.
Source: https://habr.com/ru/post/324864/
All Articles