Functional programming and c ++ in practice

Functional programming (further OP) is now in fashion. Articles, books, blogs. At each conference there are necessarily presentations where people talk about the beauty and convenience of the functional approach. For a long time I looked at him from afar, but it was time to try to put it into practice. After reading a fair amount of theory and putting the big picture in my head, I decided to write a small application in a functional style. Since at the moment I am a c ++ programmer, I will use this wonderful language. I will take as a basis the code from my previous article , i.e. My example would be a simplified 2D simulation of physical bodies.

Statement

I am by no means an expert. My goal was to try to understand the OP and its scope. In this article, I will describe step by step how I turned OOP code into a kind of functional using c ++. Of the functional programming languages, I had experience only with Erlang. In other words, here I will describe the process of my training - perhaps it will help someone. And of course, I welcome constructive criticism and comments. I even insist that you leave comments - what I did wrong, what can be improved.

Introduction

In the article, I will not tell the theory of FP - there is a great variety of material in the network, including on the habr. Although I tried to bring the program closer to a pure OP, I could not do it 100%. In some cases, due to inexpediency, in some - due to lack of experience. For example, the render is made in the usual OOP style. Why? Because one of the principles of FP is immutable data (immutable data) and the lack of state. But for DirectX (the API I use) you need to store buffers, textures, devices. Of course, it is possible to create everything anew each frame, but it will be damn long (we’ll talk about performance at the end of the article). Another example is that in LF, lazy evaluation is often used. But I did not find a place in the program to use them, so you will not find them.

Main

The source code is in this commit .
')
Everything starts in the main() function - here we create the shapes ( struct Shape ) and run an infinite loop, where we will update the simulation. Immediately you should pay attention to the design of the code - I write the function in a separate cpp file and declare it extern in the place of use - so I don’t need to create a separate header file or even a separate type, which positively affects the compilation time and generally makes the code more readable: one function - one file.

So, in the main function, we created a data set and now we need to pass it on to the updateSimulation() function.

Update Simulation

This is the heart of our program and precisely the part to which the FP was applied. The signature looks like this:

 vector<Shape> updateSimulation(float const dt, vector<Shape> const shapes, float const width, float const height); 

We accept a copy of the original data and return the new vector with the modified data. But why a copy, and not a constant link? After all, I wrote above that one of the principles of FP is the immutability of data and const reference guarantees this. This is true, but the next most important principle is the purity of functions (pure function) - i.e. no side effects and a guarantee that the function will return the same values ​​with the same input data. But, receiving the link, we cannot guarantee this. Let us consider an example. Suppose we have some function that accepts a constant link:

 int foo(vector<int> const & data) { return accumulate(data.begin(), data.end(), 0); } 

And call this:

 vector<int> data{1, 1, 1}; int result{foo(data)}; 

Although foo() accepts const & , the data itself is not constant, which means that it can be changed before and at the time of the call to accumulate() , for example, by another thread. That is why all the data should come as a copy.

In addition, in order to maintain the principle of data immutability, all fields of all user types must be constants. This is, for example, the class of a vector:

 struct Vec2 { float const x; float const y; Vec2(float const x = 0.0f, float const y = 0.0f) : x{ x }, y{ y } {} // member functions } 

As you can see, the state is set when the object is created and never changes! Those. even a state can be called a stretch - just a data set.

Let's go back to our updateSimulation() function. It is called as follows:

 shapes = updateSimulation(dtStep, move(shapes), wSize.x, wSize.y); 

It uses the semantics of the move ( std::move() ) - this allows you to get rid of unnecessary copies. In our case, however, this has no effect, since we operate on primitive types, and moving is equivalent to copying.

There is another interesting point - our function returns a new data set, which we assign to the old variable shapes , which, in fact, is a violation of the principle of lack of state. However, I believe that we can change the local variable without fear - it will not affect the result of the function, since this change remains encapsulated inside this function.

The function body looks like this:


Here we again receive copies of the data and return a copy of the changed data. In my opinion, the code looks very clear and easy to understand - here we call function by function, passing modified data like a pipeline.

Next, I will describe the simulation algorithm itself and how I had to modify it to fit into the functional style, but without formulas. Therefore it should be interesting.

Calculate Positions And Bounds

Another clean function that works with a copy of the data and returns new ones. As follows:


The standard library has been supporting the OP for many years. The for_each algorithm is a higher order function, i.e. function that accepts other functions. In general, stl very rich in algorithms, so knowledge of the library is very important if you write in a functional style.

In the following code there are a couple of interesting points. The first is a link to a vector in the lambda capture list. Yes, I tried to do without links at all, but in this place it is just necessary. And, as I wrote above, this should not violate the principles, since the link is taken to a local vector, i.e. closed to the outside world. Here one could do without it, using the for loop, but I went in the direction of visualization and readability.

The second point is related to the cycle itself. Again, since there should be no states, there should be no cycles, because the loop counter is a state. There are no cycles in pure FP; they are replaced by recursion. Let's try rewriting a function using it:


We got rid of the links! But instead of one function, there are two. And, most importantly, readability has deteriorated (at least, for me - a man who grew up in a traditional PLO). An interesting point - here we use the so-called tail recursion (tail recursion) - in theory, in this case, the stack should be cleared. However, I did not find in the c ++ standard records of such behavior, so I can not guarantee the absence of stack overflow. Considering all the above, I decided to dwell on cycles and you will not see more recursion in this article.

Calculate Cells Ranges and Fill Grid

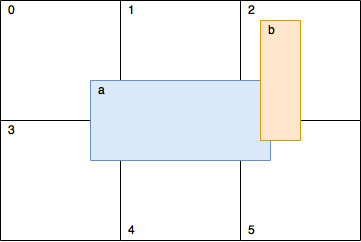
To speed up the calculations, I use a 2D grid divided into cells. Being in this grid, an object can occupy several cells, as shown in the picture:



The function calculateCellsRanges() calculates the cells occupied by the figure and returns the changed data.

In the fillGrid() function, we fill each cell (in our example, the cell is just std::vector ) with corresponding shapes. Those. if the cell contains nothing, an empty vector will be returned. Later in the code, we will run through each cell, and check inside it every figure with each other for intersection. But in the figure you can see that figure a and figure b are (besides other cells) both in cell 2 and cell 5. This means that the check will be performed twice. Therefore, we will add logic that will say whether verification is necessary. Knowing the rows and columns make it trivial.

Solve collisions

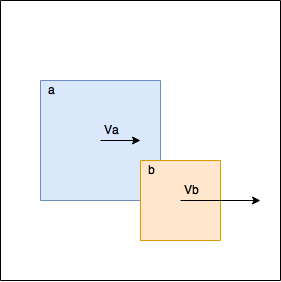
In my previous article I used the following technique - if it turned out that the objects overlapped, we moved them away from each other.



Those. we made it so that the objects a and b ceased to touch. This added a lot of complexity - you had to re-calculate the bounding box every time we moved an object. To avoid multiple rearrangements, we introduced a special battery, into which we put all the permutations, and later used this battery only once. One way or another, we had to introduce mutexes for synchronization, the code was complicated and in this form was not suitable for a functional approach. In a new attempt, we will not move objects at all, moreover, we will produce calculations only if they are really necessary. In the picture, for example, calculations are not needed, because figure b moves faster than figure a , i.e. they move away from each other, and sooner or later they will no longer come into contact without our participation. Of course, this is physically implausible, but if the speeds are small and / or a small simulation step is used, then it looks quite normal. If calculations are needed, we consider the changes in the velocities that occurred during the collision and return these speeds together with the figure identifier.

Apply Velocities

With speed changes in hand, the applyVelocities() function simply summarizes them and applies them to the object. Again, the plausibility is not in question and, quite possibly, artifacts will appear under certain conditions, but I did not notice problems with this approach on my test data. And the goal of the experiment was not at all plausible.

Result

After these simple steps we will have new data that we will pass on to the renderer. Then all over again, and so on to infinity. As proof, it all works here is a short video:


The code is in this commit .

Conclusion

AF requires a restructuring of thinking. But is it worth it? Here are my pros and cons.

Behind:

• Readability code. Together with SRP, the code is very easy to understand.
• Testability Since the result of the function does not depend on the environment, we already have everything necessary for testing.
• In my opinion - the most important point. Great parallelization capability. Each (yes, every!) Function in our example can be called multiple threads safely! No synchronization tools!

Vs:

• Only one fly in the ointment — not even a spoon, a ladle. Performance. Remember, in the last article in one stream with a 2D grid, we could simulate 8000 figures. Now only 330. Three hundred and thirty, Karl!

I worked for ten years in game devise, trying to squeeze the maximum out of each line. For the 3D engine, a functional approach in the form in which suicide was undoubtedly presented today. However, c ++ is not only game dev. I can not say for sure, but intuition suggests that for most applications, the AF will prove to be quite a competitive technique.

With a few techniques in hand, why not try to combine them? In my next article I will try to cross the OOP, DOD and OP. I do not know the result, but I already see places where you can significantly increase productivity. So stay in touch - it should be interesting.