Using the example of the Monty Hall paradox, we will see what is common between statistics and intuition, and how data visualization can help make the right decision based on statistical evaluation.

The Complexity of Monty Hall Paradox

Paraty Monty Hall got its name from the leading television show "Let's Make a Deal". Game situation:

There are three doors in front of the player, one of which is a prize. The player chooses one of them without opening. After that, the presenter opens one of the two remaining doors. The facilitator knows which of the doors is the prize, and always opens the door, for which there is no prize. Next, the player is invited to change the initially selected door to another, which remains closed. Question: Does the player's chances increase when the selected door changes?

The paradox is that it seems intuitively that changing the door gives nothing. The prize is either behind one door or after another. The situation is symmetrical, and the probabilities are the same. However, probability theory shows that changing the door doubles the chances of winning.

To arrive at a statistically correct solution, the player must:

1. Mentally move from the choice of one of the two doors to the choice of one of the two strategies: "stay" (leave the door that was originally selected) and "switch" (change the door to another).
2. Build a statistical model of the game situation and evaluate both strategies.
3. Based on statistical estimates, discard the originally selected door.

The first step is key. If you stay at the level of choice of doors, then nothing will come out, because the prize, one way or another, is behind one of the two doors. And they look the same - the situation seems to be symmetrical. You can not change the door and win, you can change the door and lose. Perhaps changing the door increases the chances of success, but does not guarantee it. Taking the first step, the player should not confuse the "increased chances" and "guaranteed winnings".

The second step is even more difficult: to build and apply a statistical model of the problem. The chain of reasoning can be like this.

First, the player chooses one of the three doors. By condition, the prize is placed for any of them with the same probability. In the first step, the probability of choosing a prize is 1/3. The figure below shows the decision tree after the initial selection of the player. The door, behind which the prize is painted over:

Then the leader opens one of the doors not selected by the player. It seems to the player that the presenter chooses the door to open. However, this is not always the case. The behavior of the leader is caused by the first choice of the player:

• If the player immediately chose a door with a prize, then the moderator can choose either of the two closed ones. There is no prize for any of them.
• If a player chooses a door without a prize, the presenter always opens one door. The door, behind which the prize, the lead can not open under the terms of the game.

The probability that the prize behind the door, which the presenter has left closed, is calculated using the conditional probability formula. And these probabilities differ for different outcomes, as the decision tree shows. Closed doors, behind which the prize is painted over:

The player summarizes the probabilities for each strategy and gets their statistical evaluation. The figure shows that the probability of winning when changing the door (strategy "switch") is two times higher:

After the strategies are evaluated, the player must refuse the initial selection. It is difficult in itself. The player will strive to keep the initial selection, as this is easier. For example, a potential buyer is much more likely not to disable the included service by default, rather than turn it on. In general, this leads to a systematic deviation of the players' behavior from the rational.

Difficulties in applying statistical thinking

The problems associated with the use of statistical thinking and rational thinking are discussed in general in David Kahneman's book "Think slowly, solve quickly." Studies by Kahneman and his colleagues have shown that a person is prone to make mistakes in situations when even simple mathematical calculations need to be done, not to mention estimating probability.

Kahneman introduces the concept of two systems. System 1 is a "fast", intuitive, heuristic thinking. The person uses it, for example, to determine the mood by the expression of the face or when assessing the traffic situation when the car is driving. System 1 is an automatic, almost instantaneous response, and works in most everyday situations.

System 2 - "slow", rational, mathematical and statistical thinking. This system connects with effort. A person must realize that the automatic decision is wrong, think about it and make calculations.

The key problem is that in a situation where you need to think, a person relies on an automatic solution offered by system 1. And this system draws conclusions, first of all, on the basis of similarity of options. In the Monty Hall paradox, after the presenter opened one of the doors, the remaining two look the same, and the moderator’s behavior is carefully disguised. The situation seems to be symmetrical, and the probabilities are the same. System 1 has nothing to cling to to notice probable asymmetry. System 2 has no time to connect. Moreover, the leader tries in different ways to confuse the player.

System 1 trains on multiple repetitions of situations, bringing the choice to automatism (face recognition, car driving). A person sees a similar situation, something that is familiar to him, and makes a choice that was previously successful in similar situations.

System 2 implies that a person begins to analyze a situation in order to make a decision. In the case of statistical problems, the correct answer is not obvious. To come to him, a person must analyze the data, make calculations and select the highest values ​​of statistical indicators.

The general between intuition and statistics

The basic idea of ​​David Kaneman is that system 1 (intuitive) and system 2 (rational) are different. In general, it is, however, in relation to statistics, there is a similarity between them.

Suppose that all the participants in the Monty Hall show have gathered to discuss the results of their participation in the show. The participants broke into two groups: those who stayed with the originally chosen door and those who changed the door. According to statistics, counting participants and their results will show that those participants who changed the door, won more often . If there are many participants in both groups, the share of winners in the group who changed the door will be approximately two times higher than in the other.

A sufficient number of participants, under which the statistical regularity will be visible, is determined by the law of large numbers. The more players take part in the meeting, the more the results of calculations of their successes and failures will correspond to theoretical ones. In other words, the statistics starts working when the game has been repeated by different participants many times. If such a community of players existed, then over time they would come to the right strategy.

Thus, in statistical calculations, system 2 relies on the law of large numbers — a sufficiently large (ideally infinite) number of tests. But also system 1 a large number of tests allows you to make the right decisions. Repeated repetition brings a person’s ability to automatism.

Rules for two systems:

• System 1: it was right for me many times in similar cases, so it will be true now.
• System 2: it was right for many other people in similar cases, so it will be true now.

We can say that the calculation of probability reflects the collective experience of all the real and possible participants in the game Monty Hall. For situations of individual choice of strategies, statistics act as a collective intuition. It remains to make the statistics visible with the help of a suitable visualization.

The chart-scale for visualization of theoretical and frequency probability

Using the example of the Monty Hall paradox, we modeled the choice of the right strategy by a person involving statistical calculations. In general:

• There may be more than two strategies.
• Theoretical calculations of probability may be missing or require verification. Then you have to try all the strategies and determine the frequency probability for each.
• Externally, the various options may not differ in any way (the doors in the game Monty Hall look the same - visual symmetry).

If you set the task to help the player win, and not to confuse him, as in a show, then in the data visualization or user interface you can add “doors” between which the player chooses diagrams. On such a chart, the scale sets the gradation of the magnitude change, and a scale of the actual value is superimposed on the scale by analogy with a thermometer.

On the chart-scale, it is convenient to combine the theoretical, expected number of wins (grayed out) and the actual after all previous games (a narrow black bar). The actual value changes after each decision taken on the choice of one of two strategies and is maintained throughout the entire series of games:

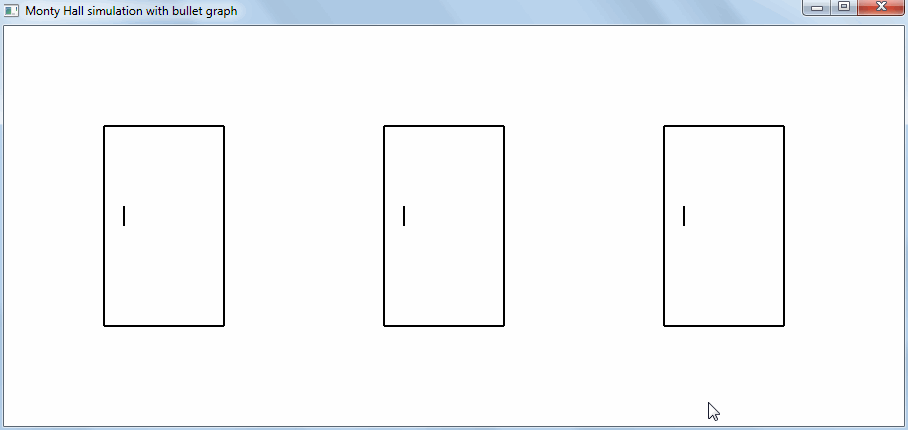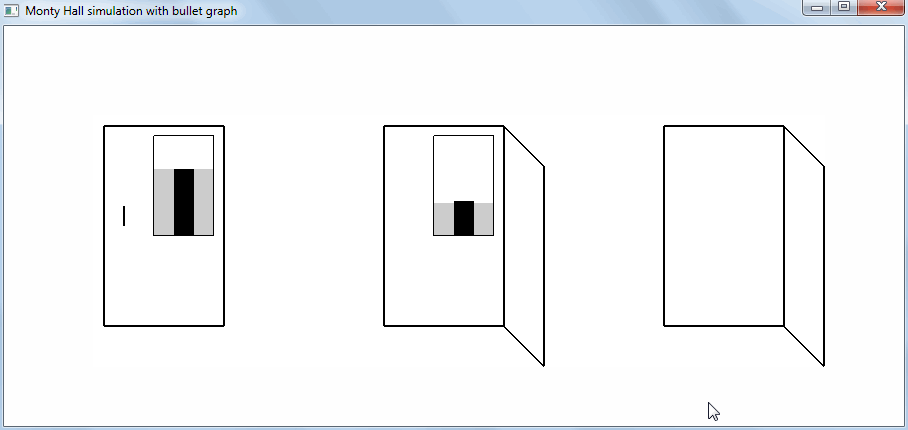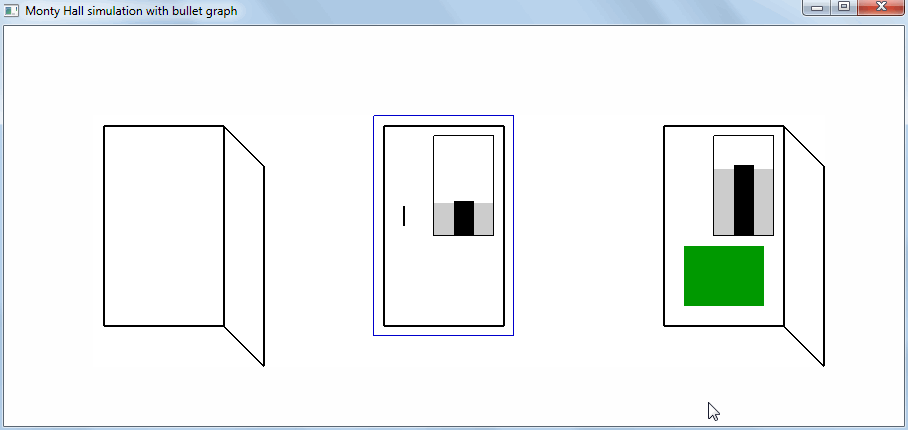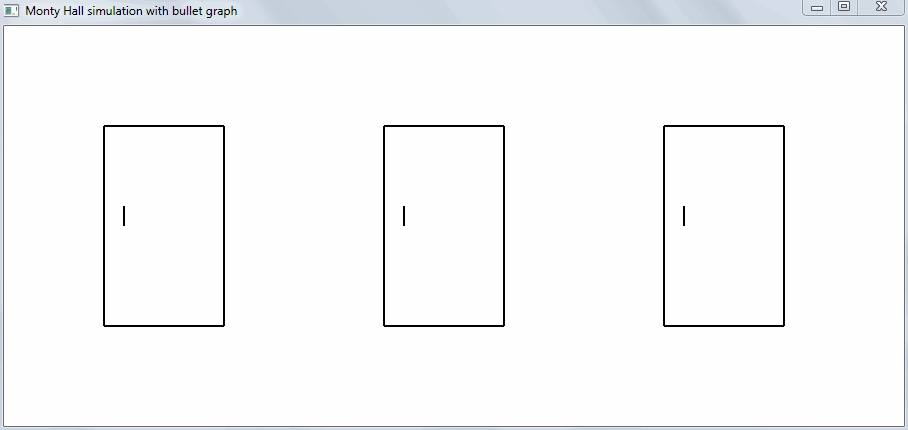
Thus, suitable visualization of statistical data helps a person to choose the right strategy. For example, in an interface that looks like a prototype, an interface element that matches a strategy can be labeled with a statistical widget that looks like a scale chart. Image of actual data is useful if the user chooses between approximately equally successful strategies. It allows him to quickly come to the conclusion:

It seems more often successful

findings

• A person is inclined to ignore or incorrectly use the calculation of probability and statistics when choosing a strategy.
• Statistics can be viewed as a collective intuition - multiple successful test outcomes of other people.
• If the statistics are correctly visualized, then this will increase the efficiency of the choice of a strategy by a person.

Links

• Monty Hall game
• Pigeons brutalize Monty Hall's paradox better than people.
• Monty Hall Paradox Check
• Think slowly ... decide quickly. D. Kaneman
• Scale Chart (Bullet Graph)
• PyOpenGL simulation of Monty Hall game with diagrams on GitHub