FSE coding
Finite State Entropy (FSE) is an entropy coding algorithm, somewhat similar to both the Huffman algorithm and arithmetic coding . At the same time, he took the best of both of them: it works as fast as a Huffman one, and with a compression ratio like that of arithmetic coding.
FSE belongs to the ANS ( Asymmetric Numeral Systems ) codec family, invented by Yarek Duda . Based on his research, Ian Collett developed an optimized version of the algorithm, later called FSE.
Ian Colett’s notes are not easy to understand, so I’ll present an explanation in a slightly different order, more easy to understand, in my opinion.
')

Recall how the Huffman algorithm works.
Suppose we have a certain message consisting of characters in the following proportions:
With such a good distribution, you can encode characters as follows:

For A, 1 bit is needed; for B, 2 bits; C and D - 3 bits.
If the probability distribution is less appropriate, for example:
A: 40%; B: 30%; C: 15%; D: 15%, then according to the Huffman algorithm, we get exactly the same character codes, but the compression will not be as good.
The degree of compression of the message is described by the following formula: where
It is known that for entropy codecs the optimal compression quality is described by the Shannon formula: . If we compare this with the previous formula, it turns out that
In the Huffman algorithm, the number of bits is rounded to the whole, which negatively affects the degree of compression.
The algorithm of arithmetic coding uses a different approach, which allows not to round off and thereby get closer to the “ideal” compression. But it works relatively slowly.
The FSE algorithm is a cross between the previous two approaches. It uses a variable number of bits (sometimes more, sometimes less) to encode a character so that on average it turns out bit per character.
Consider an example. Let the characters in the message to be encoded are in the following proportion:
A : 5; B : 5; C : 3; D : 3
We call these numbers the normalized frequencies and denote
- the sum of (normalized) symbol frequencies.
In our example, N = 16. For fast operation of the algorithm, it is necessary that N be a power of two. If the sum of the frequencies of the symbols is not equal to the power of two (almost always), then the frequencies need to be normalized - proportionally decrease (or increase) them so that the power of the power of two is combined. More on this later.
Take a table of N columns and enter message symbols there so that each character is encountered exactly as many times as its frequency. The order is not important yet.
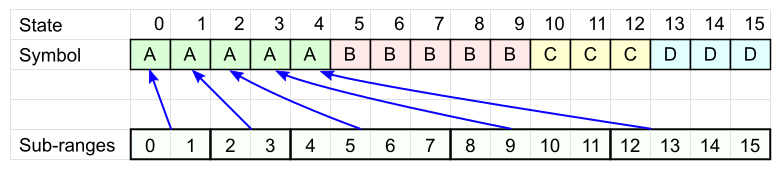
Each symbol A has its own range of cells ( Sub-ranges in the figure): the size of each range should be a power of two (for speed), in total they should cover all N cells (for now, it doesn’t matter how these ranges are located).
Similarly, for each of the other characters, we define our own set of ranges.
For symbol D there will be 3 ranges:
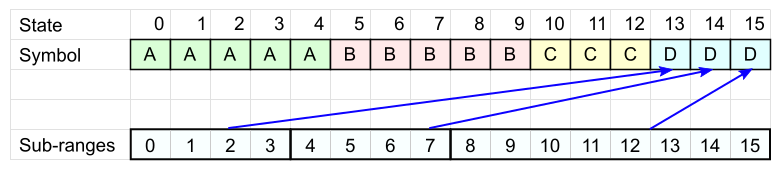
The code table is ready. Encode with its help the word "BCDA".
Decoding is performed in reverse order - from the last encoded character to the first.
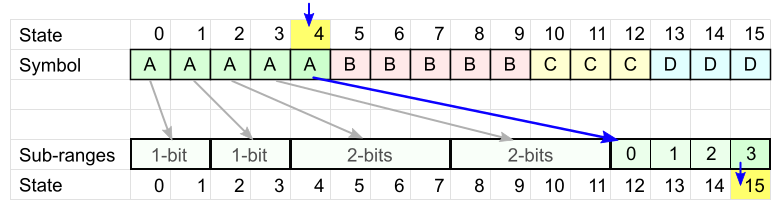
The theory tells us that the coding will be more optimal if the same characters are distributed more evenly in the table.
This is necessary so that the state does not “stagnate” in large intervals, losing the extra bit.
It may seem that it would be nice to fall into small intervals all the time (on the left side of the table). But in this case, other characters will more often fall into large intervals - in the end it will only get worse.
Finally, we move from theory to code. To begin, let us figure out how to calculate during coding, in what interval the current state falls and how many bits need to be written.
For coding, we need to split a table of size N (equal to some power of two) into
For example, if N = 16 and we need 6 intervals, then the partition will be: 2 + 2 + 2 + 2 + 4 + 4 - four “small” intervals of size 2 1 and two “large” sizes of 2 2 .

Simply calculate the size of a large interval - this is the smallest power of two, such that
Accordingly,
Let us return to obtaining
Now we will find under what condition the state state falls into a large interval.
To determine the boundary between small and large intervals, multiply the number of small intervals by their size:
It turns out that the state
The size of the interval we hit determines how many lower bits from the current state need to be recorded during coding. If the condition above is satisfied, then
Instead of the comparison operation, apply a hack with a difference shift by a sufficiently large number:
The absence of a condition in this expression allows the processor to more effectively use internal parallelism. (The variable count corresponds to the q character in the preceding formulas.)
As a result, the encoding function takes the following form:
All that can be calculated in advance, put in the table:
Note that
As you can see, the calculations are very simple and fast.
Decoding will look accordingly:
Even easier!
The real code can be found here . There you can also find how the
Above, we proceeded from the assumption that the sum of the frequencies of the symbols
In this case, it is necessary to take into account that the sum of the frequencies of the symbols is equal to the size of the code table. The larger the table, the more accurate the symbol frequencies will be and the better the compression will be. On the other hand, the table itself also takes up a lot of space. To estimate the size of the compressed data, you can use the Shannon formula ,too boldly assuming that the compression tends to the ideal, and in this way to choose the optimal tables.
In the process of frequency normalization, many small problems can arise. For example, if some characters have a very, very small probability, then the smallest representable frequency 1 / N may be too inaccurate approximation, but there is no less. One of the approaches in this case is to assign
There are both fast heuristic algorithms for frequency normalization and slow, but more accurate ones. The choice is yours.
Let's consider the situation when we need to encode numeric values from a potentially large range, for example, from -65536 to +65535. At the same time, the probability distribution of these numbers is highly uneven: with a large peak in the center and very small probabilities at the edges, as in the picture. If you encode each value as a separate character, the table will be of unimaginable size.
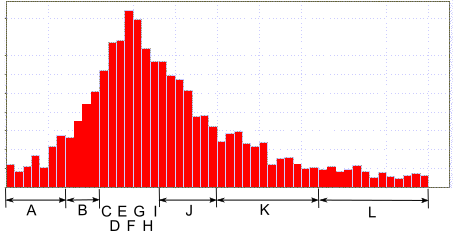
In this situation, you can designate a single range of values with one symbol. With FSE, we will encode only the symbol itself, and the offset in the range will be written “as is”, according to the size of the range.
This technique allows us to make the code tables more or less compact.
This example demonstrates that the choice of the alphabet is highly dependent on your data. It is necessary to apply a little imagination to make the coding the most optimal.
If different parts of the data have a different frequency distribution, then it is better to use different tables for their coding.
In this case, heterogeneous data can be encoded, alternately using different tables! A state from one table is used to encode the next character by another table. The main thing is that you can repeat the same order when decoding. Tables must also be the same size.
For example, let your data be a sequence of the form " command - number - command - number ... ". You always know that there will be a number after the command, and this determines the order in which the tables are used.
If you encode the data from the end to the beginning , then when decoding (from the beginning to the end) it will be clear what will be followed by and, accordingly, which table to use for decoding the next element.
As mentioned above, the code table needs to be saved along with the data in order to decode it. It is desirable that the table does not take up much space.
Let's see what fields are in the dTable table:
Total: 4 bytes for each character. A lot.
But if you think about it, instead of the dTable table you can only store normalized symbol frequencies. For example, if the size of the code table is 2 8 = 256, then 8 bits per character will be more than enough.
Knowing the frequency, you can build exactly the same dTable, as when encoding.
At the same time, I advise you to make sure that the algorithm does not use float (there are differences on different processors with it, it is better to use a fixed point), use only stable_sort and similar measures for reliable reproducibility of the result.
By the way, these tables can also be compressed somehow. ;)
We at Playrix use FSE to encode vector animations. Delta between frames consist of a set of small values with a distribution peak near zero. The transition from Huffman to FSE made it possible to reduce the size of animations by about one and a half times. Compressed data is stored in memory, unpacking is done “on the fly” with simultaneous playback. FSE allows you to do this very effectively.
Now that you have figured out how FSE works, for more understanding, I recommend reading the Jan Collet blog (in English) for details:
The code on GitHub (by Jan Collet): https://github.com/Cyan4973/FiniteStateEntropy .
FSE belongs to the ANS ( Asymmetric Numeral Systems ) codec family, invented by Yarek Duda . Based on his research, Ian Collett developed an optimized version of the algorithm, later called FSE.
Ian Colett’s notes are not easy to understand, so I’ll present an explanation in a slightly different order, more easy to understand, in my opinion.
')

Comparison with existing algorithms
Recall how the Huffman algorithm works.
Suppose we have a certain message consisting of characters in the following proportions:
A : 50%; B : 25%; C : 12.5%; D : 12.5%
With such a good distribution, you can encode characters as follows:

For A, 1 bit is needed; for B, 2 bits; C and D - 3 bits.
If the probability distribution is less appropriate, for example:
A: 40%; B: 30%; C: 15%; D: 15%, then according to the Huffman algorithm, we get exactly the same character codes, but the compression will not be as good.
The degree of compression of the message is described by the following formula: where
p i is the frequency with which the character is encountered in the message, b i is the number of bits for encoding this character.It is known that for entropy codecs the optimal compression quality is described by the Shannon formula: . If we compare this with the previous formula, it turns out that
b i should be equal to . Most often, the magnitude of this logarithm is obtained as non-integer .Incomplete number of bits - what to do about it?
In the Huffman algorithm, the number of bits is rounded to the whole, which negatively affects the degree of compression.
The algorithm of arithmetic coding uses a different approach, which allows not to round off and thereby get closer to the “ideal” compression. But it works relatively slowly.
The FSE algorithm is a cross between the previous two approaches. It uses a variable number of bits (sometimes more, sometimes less) to encode a character so that on average it turns out bit per character.
How does FSE work
Consider an example. Let the characters in the message to be encoded are in the following proportion:
A : 5; B : 5; C : 3; D : 3
We call these numbers the normalized frequencies and denote
q i .- the sum of (normalized) symbol frequencies.
In our example, N = 16. For fast operation of the algorithm, it is necessary that N be a power of two. If the sum of the frequencies of the symbols is not equal to the power of two (almost always), then the frequencies need to be normalized - proportionally decrease (or increase) them so that the power of the power of two is combined. More on this later.
Take a table of N columns and enter message symbols there so that each character is encountered exactly as many times as its frequency. The order is not important yet.

Each symbol A has its own range of cells ( Sub-ranges in the figure): the size of each range should be a power of two (for speed), in total they should cover all N cells (for now, it doesn’t matter how these ranges are located).
Similarly, for each of the other characters, we define our own set of ranges.
For symbol D there will be 3 ranges:

The code table is ready. Encode with its help the word "BCDA".
- The first character is " B ". Choose any table cell with this symbol. The cell number is our current state .

Current state = 5 . - Take the next character - " C ". We look at the code table for C and check which of the intervals our current state has hit.
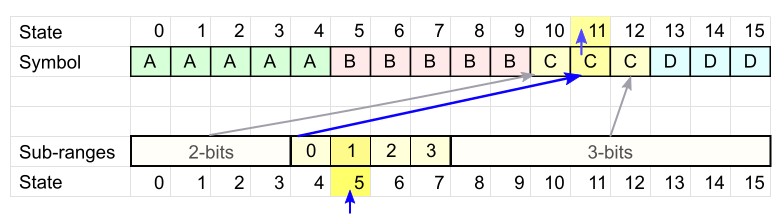
In our case, state 5 fell into the second interval.
We write the offset from the beginning of this interval. In our case, it is 1 . To record the offset, you will need 2 bits - according to the size of the range in which our state fell.
The current range corresponds to the character C in cell 11, then the new state = 11 . - Repeat point 2 for each subsequent symbol: select the desired table, determine the range, write the offset, we get a new state.
For each character, only an offset in the interval is recorded. For this, a different number of bits is used, depending on whether we are in the “large” or “small” interval. On average, the number of bits per character will tend to the value . Proving this fact requires a complex theory , so just believe. - When the last character is encoded, we will have the final state. It needs to be saved, decoding will begin with it.
Decoding is performed in reverse order - from the last encoded character to the first.

- We have the final state (4), and it uniquely identifies the last encoded character (A).
- Each state corresponds to an interval in the code table. We read the required number of bits according to the size of the interval (2 bits) and get a new state (15), which defines the next character.
- Repeat point 2 until we decode all characters.
Decoding ends, either when the encoded data ends, or when a special stop character is encountered (requires an additional character in the alphabet).
The distribution of characters in the table
The theory tells us that the coding will be more optimal if the same characters are distributed more evenly in the table.

This is necessary so that the state does not “stagnate” in large intervals, losing the extra bit.
It may seem that it would be nice to fall into small intervals all the time (on the left side of the table). But in this case, other characters will more often fall into large intervals - in the end it will only get worse.
Optimization
Finally, we move from theory to code. To begin, let us figure out how to calculate during coding, in what interval the current state falls and how many bits need to be written.
For coding, we need to split a table of size N (equal to some power of two) into
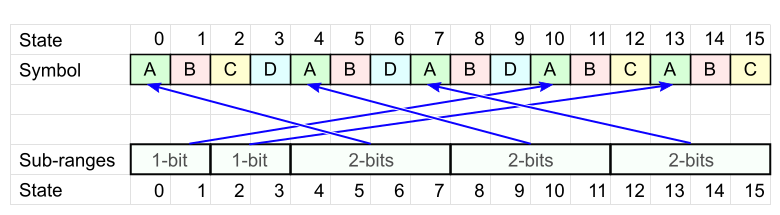
q i intervals. The sizes of these intervals will also be powers of two: 2 ^ maxbit and 2 ^ (maxbit-1) - let's call them “big” and “small”. Let the small intervals be to the left, and the large intervals to the right, as in the figure below.For example, if N = 16 and we need 6 intervals, then the partition will be: 2 + 2 + 2 + 2 + 4 + 4 - four “small” intervals of size 2 1 and two “large” sizes of 2 2 .

Simply calculate the size of a large interval - this is the smallest power of two, such that
2^maxbit >= N / q .Accordingly,
maxbit = log 2 (N) - highbit(q) , where highbit is the number of the highest nonzero bit.Let us return to obtaining
q intervals. First, we divide the table into “large” intervals: (N / 2 ^ maxbit) pieces, then several of them will be divided in half. Separation of the interval increases their total number by 1, therefore, “divide” requires q - (N / 2 ^ maxbit) large intervals. Accordingly, the number of small intervals will be (q - (N / 2 ^ maxbit)) * 2.Now we will find under what condition the state state falls into a large interval.
To determine the boundary between small and large intervals, multiply the number of small intervals by their size:
(q - (N / 2^maxbit))*2 * 2^(maxbit-1) = (q * 2^maxbit) - N;It turns out that the state
state falls into a large interval providedN + state >= q * 2^maxbit, otherwise - in small .The size of the interval we hit determines how many lower bits from the current state need to be recorded during coding. If the condition above is satisfied, then
nbBitsOut = maxbit , otherwise ( maxbit - 1). The remaining status bits will determine the slot number.Instead of the comparison operation, apply a hack with a difference shift by a sufficiently large number:
nbBitsOut = ((maxbit << 16) + N + state - (count << maxbit) ) >> 16;The absence of a condition in this expression allows the processor to more effectively use internal parallelism. (The variable count corresponds to the q character in the preceding formulas.)
As a result, the encoding function takes the following form:
// nbBitsOut = ((maxBitsOut << 16) + N + state - (count << maxBitsOut)) >> 16; // nbBitsOut state bitStream: bitStream.WriteBits(state, nbBitsOut); interval_number = (N + state) >> nbBitsOut; // : state = nextStateTable[deltaFindState[symbol] + interval_number]; All that can be calculated in advance, put in the table:
symbolTT[symbol].deltaNbBits = (maxBitsOut << 16) - (count << maxBitsOut); Note that
state is always used as N + state . If in the nextStateTable also store N + next_state , the function will take the following form: nbBitsOut = (N_plus_state + symbolTT[symbol].deltaNbBits) >> 16; bitStream.WriteBits(N_plus_state, nbBitsOut); // : N_plus_state = nextStateTable[symbolTT[symbol].deltaFindState + (N_plus_state >> nbBitsOut)]; As you can see, the calculations are very simple and fast.
Decoding will look accordingly:
// outputSymbol(decodeTable[state].symbol); // , nbBits = decodeTable[state].nbBits; // offset = readBits(bitStream, nbBits); // : + state = decodeTable[state].subrange_pos + offset; Even easier!
The real code can be found here . There you can also find how the
symbolTT decodeTable. tables are filled symbolTT decodeTable.About frequency symbol normalization
Above, we proceeded from the assumption that the sum of the frequencies of the symbols
q i is equal to the power of two. In general, this is certainly not the case. Then you need to proportionally reduce these numbers so that in total they give a power of two.In this case, it is necessary to take into account that the sum of the frequencies of the symbols is equal to the size of the code table. The larger the table, the more accurate the symbol frequencies will be and the better the compression will be. On the other hand, the table itself also takes up a lot of space. To estimate the size of the compressed data, you can use the Shannon formula ,
In the process of frequency normalization, many small problems can arise. For example, if some characters have a very, very small probability, then the smallest representable frequency 1 / N may be too inaccurate approximation, but there is no less. One of the approaches in this case is to assign
q i = 1 to such characters immediately, place them at the end of the code table (so it is more optimal), and then deal with the other characters. Rounding values to the nearest integer may also not be the best option. This and many other nuances are well written by Jan Collet ( 1 , 2 , 3 , 4 ).There are both fast heuristic algorithms for frequency normalization and slow, but more accurate ones. The choice is yours.
Choosing a data model
Let's consider the situation when we need to encode numeric values from a potentially large range, for example, from -65536 to +65535. At the same time, the probability distribution of these numbers is highly uneven: with a large peak in the center and very small probabilities at the edges, as in the picture. If you encode each value as a separate character, the table will be of unimaginable size.

In this situation, you can designate a single range of values with one symbol. With FSE, we will encode only the symbol itself, and the offset in the range will be written “as is”, according to the size of the range.
This technique allows us to make the code tables more or less compact.
This example demonstrates that the choice of the alphabet is highly dependent on your data. It is necessary to apply a little imagination to make the coding the most optimal.
Mixed coding
If different parts of the data have a different frequency distribution, then it is better to use different tables for their coding.
In this case, heterogeneous data can be encoded, alternately using different tables! A state from one table is used to encode the next character by another table. The main thing is that you can repeat the same order when decoding. Tables must also be the same size.
For example, let your data be a sequence of the form " command - number - command - number ... ". You always know that there will be a number after the command, and this determines the order in which the tables are used.
If you encode the data from the end to the beginning , then when decoding (from the beginning to the end) it will be clear what will be followed by and, accordingly, which table to use for decoding the next element.
About table entry
As mentioned above, the code table needs to be saved along with the data in order to decode it. It is desirable that the table does not take up much space.
Let's see what fields are in the dTable table:
unsigned char symbol; // 256 unsigned short subrange_pos; // unsigned char nbBits; // Total: 4 bytes for each character. A lot.
But if you think about it, instead of the dTable table you can only store normalized symbol frequencies. For example, if the size of the code table is 2 8 = 256, then 8 bits per character will be more than enough.
Knowing the frequency, you can build exactly the same dTable, as when encoding.
At the same time, I advise you to make sure that the algorithm does not use float (there are differences on different processors with it, it is better to use a fixed point), use only stable_sort and similar measures for reliable reproducibility of the result.
By the way, these tables can also be compressed somehow. ;)
Epilogue
We at Playrix use FSE to encode vector animations. Delta between frames consist of a set of small values with a distribution peak near zero. The transition from Huffman to FSE made it possible to reduce the size of animations by about one and a half times. Compressed data is stored in memory, unpacking is done “on the fly” with simultaneous playback. FSE allows you to do this very effectively.
Links
Now that you have figured out how FSE works, for more understanding, I recommend reading the Jan Collet blog (in English) for details:
- Finite State Entropy - A new breed of entropy coder
- FSE decoding: how it works
- Huffman, a comparison with FSE
- A comparison of Arithmetic Encoding with FSE
- FSE: Defining optimal subranges
- FSE: distributing symbol values
- FSE decoding: wrap up
- FSE encoding: how it works
- FSE tricks - Memory efficient subrange maps
- Better normalization, for better compression
- Perfect Normalization
- Ultra-fast normalization
- Taking advantage of unequalities to provide better compression
- Counting bytes fast - little trick from FSE
The code on GitHub (by Jan Collet): https://github.com/Cyan4973/FiniteStateEntropy .
Source: https://habr.com/ru/post/324116/
All Articles