Theoretical foundations of spline interpolation or why IQ tests have no solution

Good time, Habr!

A lot of time has passed since I wrote my first article , and almost a year since the idea came up for the second one. Due to many circumstances (first of all - laziness and forgetfulness), this idea was never implemented before, but now I have gathered, wrote all this material and am ready to present it to your attention.

I'll start with a little intro. Being a student of the 4th, at that time, undergraduate course, I studied the course "Computer Graphics". There were a lot of different interesting (and not so) tasks there, but one thing directly sank into my soul: interpolation by cubic splines with given first derivatives at the ends of the interval. The user had to set the values ​​of the first derivatives, and the program - read and display the interpolation curve. The peculiarity and the main difficulty of the task lies in the fact that it is the first derivatives that are set, and not the second, as in the classical formulation of spline interpolation.
How I solved it, and what it eventually came to, I will explain in this article. And yes, if by the description of the task you did not understand its meaning, complexity, do not worry, I will try to reveal all this as well. So let's go.
')
Oh, no, wait a moment. Here are two numerical series:
a) 2, 4, 6, 8 ,?
b) 1, 3 ,? , 7, 9

Which numbers should stand on the spot questions and why? Are you really sure of your answer?

Interpolation

Interpolation, interpolation (from the Latin. Inter-polis - “smoothed, renewed, updated; transformed”) - in computational mathematics, a method of finding intermediate values ​​of a value from an existing discrete set of known values. (c) Wikipedia

Let me explain with examples. There are problems when we need to know, conventionally, the “distribution law” (put in quotes, since this is, generally speaking, a term from another area of ​​mathematics) of a certain parameter by several known values. Most often we are talking about the change of a certain parameter in time: the coordinates of the moving body, the temperature of the object, currency fluctuations, etc. At the same time, due to some circumstances, we did not have the opportunity to observe this parameter continuously, we could recognize its values ​​only at some specific points in time. In this case, the source data is a set of points of the form value (time) , and the goal of the task is to restore the curve passing through these points and continuously describing the change of this parameter.

It should be understood that the impossibility of continuous monitoring of the relevant parameter is usually some kind of technological limitation. With the development of technology, such situations become less and less. From modern tasks of such a plan - the trajectory of motion, for example, the rover. It is still not possible to maintain a continuous communication session (for the time being), but you want to control its movement and draw beautiful trajectories. It turns out that the specific coordinates can be found only at those moments when the connection is nevertheless established, and the entire trajectory has to be restored by the points obtained in such a way from time to time.
Another use of interpolation. Some modern TVs display an image with a picture refresh rate of up to> = 1000Hz (although these are still extremely high). Most televisions do not know how, but even so many display a picture at a frequency of 100 Hz - such a value is already quite a classic. And if you believe Wikipedia, then in the cinema "the frequency of 24 frames per second is the global standard." In order to turn 24 frames per second of the original video stream into 100 frames per second of the result, the TV uses interpolation. Namely, some algorithms in the style of “take two adjacent frames 1 and 2, calculate the difference between them and form 3 additional frames from it, which should be crammed between those two initial ones” -> frames 1, 1_1 , 1_2 , 1_3 , 2 are obtained

For further reasoning, let's take a simpler example. Let us imagine, for example, a laboratory work on geography in some sixth grade (by the way, I once really had this). It is necessary to measure the air temperature every 3 hours and record the data, and then hand in to the teacher a graph of temperature changes from the time of day. Suppose, according to the results of measurements, we have got such a label here (the data is invented randomly and does not pretend to any plausibility):



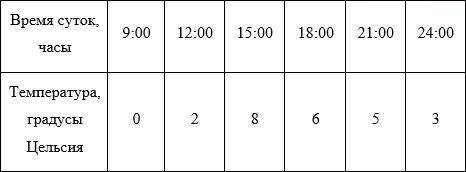
Display the data on the chart:



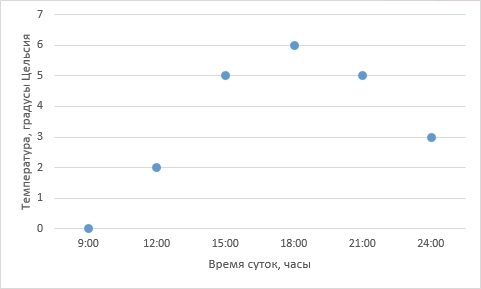
Actually, the data recorded and reflected on the graph. We came close to the interpolation problem - how can we restore a smooth curve from the points at hand?

The number of conditions and the degree of the interpolating polynomial

Can we even guarantee that such a function that connects all given points exists at all?

Yes, such a function is guaranteed to exist, and moreover, there will be infinitely many such functions. For any set of points, it will be possible to come up with as many functions as desired, which will pass through them. And here are some examples of how two points can be connected in different ways:





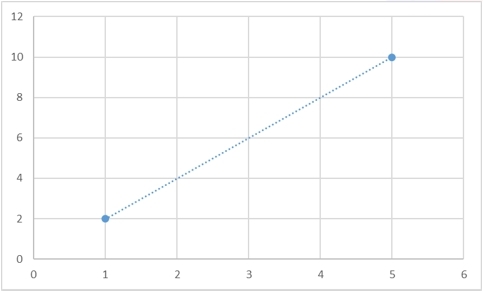
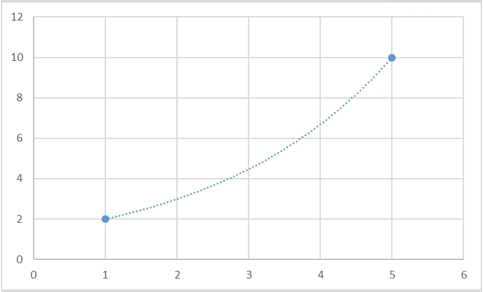
However, there is a way to define the interpolation curve uniquely. In the most classic case, a polynomial is taken as an interpolation curve:

$$$P_n (x) = a_nx ^ n + a_ {n-1} x ^ {n-1} + ... + a_1x + a_0$

In order to draw such a polynomial through unique points in a unique way, it is necessary and sufficient that the degree of the polynomial is 1 less than the number of conditions (I specifically highlighted this word, because at the end of this section I will return to this formulation). So far, for the sake of simplicity, the condition will be the coordinates of a point. Speaking in human language, it is possible to draw a straight line (a first-degree polynomial) through 2 points, a parabola (a second-degree polynomial) through 3 points, etc.

Returning to our problem with temperature - we defined 6 points in it, which means that in order to draw a polynomial in a unique way, it must be of the 5th degree



The interpolating polynomial will then look like this:

$$$ inline $ - \ frac {x ^ 5} {14580} + \ frac {13x ^ 4} {1944} - \ frac {41x ^ 3} {162} + \ frac {983x ^ 2} {216} - \ frac {2273x} {60} + $ 117 inline $

And now we should make an important remark and clarify what I meant by the “condition” . A polynomial can be defined not only by the coordinates of the points through which it passes, conditions can be any parameters of this polynomial. In the simplest case, these are really coordinates of points. But as a condition we can take, for example, the first derivative of this polynomial in any of the points. The second derivative. The third derivative. In general, any possible derivative at any point in which this polynom exists. Let me explain with an example:
The straight line can be defined uniquely, as I said, with two points:



The same line, on the other hand, can be determined by the coordinate of one point and the angle of inclination of the alpha to the horizontal:



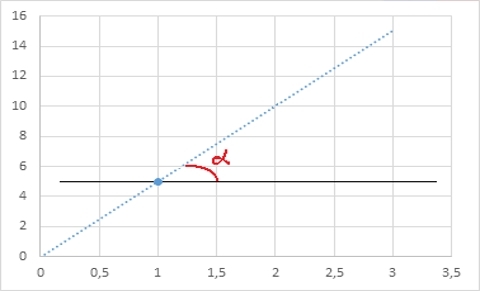
With higher degree polynomials, more complex conditions can be used (second derivative, third derivative, etc.), and each such parameter will go into a total account of the number of conditions that uniquely determine this polynomial. Not to be unfounded, here is another example:

Suppose we are given these three conditions:

$$$y (0) = 1, y '(0) = 1, y' '(0) = 2$

There are three conditions, which means we want to get a second degree polynomial:

$$$y (x) = ax ^ 2 + bx + c$

Substitute $$$x = 0 \ to y (x = 0) = c \ to c = 1$

We consider the first derivative and we consider $$$y '(x) = 2ax + b \ to [x = 0] \ to y' (x = 0) = b \ to b = 1$

We consider the second derivative and we consider $$$y '' (x) = 2a \ to [x = 0] \ to y '' (x = 0) = 2a \ to a = 1$

From here we get that our polynomial looks like this:

$$$y (x) = x ^ 2 + x + 1$

Interpolation by cubic splines

Here, on the quiet, we are going to my task. Polynomial interpolation is not the only possible interpolation method. Among all other methods, there is an interpolation method using cubic splines.

The fundamental difference between the idea of ​​spline interpolation and interpolation by a polynomial is that the polynomial is one and the spline consists of several polynomials, namely, their number is equal to the number of intervals, within which we interpolate. In the example with our air temperature, in which we have 6 points defined, we will have 5 intervals - respectively, we will have 5 polynomials, each in its own interval.

Each of these polynomials is a third-degree polynomial (strictly speaking, degrees not higher than the third, since at some interval the interpolating curve may become a quadratic parabola or even a linear function, but in general it is still a third-degree polynomial) . Writing the above formulaically, we get that all our points will be connected by a certain curve. $$$S = \ {S_1, S_2, S_3, S_4, S_5 \}$ where every $$$S_i$ - it is a polynomial of the third degree, namely:

$$$S_i (x) = ax ^ 3 + bx ^ 2 + cx + d$

Returning to what was said in the previous paragraph, in order to uniquely define one polynomial of the third degree, 4 conditions are necessary. In this problem, we have 5 polynomials, that is, to set them all, we need a total of 5 ∙ 4 = 20 conditions. And that's how they turn out:

1) The first polynomial is defined on the first and second points - these are two conditions. The second polynomial is defined on the second and third points - two more conditions. The third polynomial, the fourth, the fifth - each of them is defined on 2 points - this gives a total of 10 conditions.

2) For each intermediate point of the set (and these are 4 points with the times of 12:00, 15:00, 18:00, 21:00) the condition must be met that the first and second derivatives for the left and right polynomials must coincide. Formula:

$$$S_ {1} ^ {'} (x = 12: 00) = S_ {2} ^ {'} (x = 12: 00)$

$$$S_ {1} ^ {''} (x = 12: 00) = S_ {2} ^ {''} (x = 12: 00)$

$$$etc.$

Two such conditions on each of the intermediate points gives 8 more conditions. It should be added that we ask only the fact of equality, and what specific value they take at the same time - this is a completely different task and it is considered rather difficult.

3) There are two conditions that are not yet defined. These are the so-called “boundary conditions”, on the task of which it depends what kind of spline it will turn out. Usually set the second derivatives at the ends of the interval equal to 0:

$$$S_ {1} ^ {''} (x = 9: 00) = 0$

$$$S_ {5} ^ {''} (x = 21: 00) = 0$

If we do this, then we get the so-called “natural spline”. To calculate these splines, a huge number of libraries have already been written, take them and use any.

The difference between my task and the classical formulation of the problem, my thoughts on the task and the solution itself

And here we come to the condition of my task. The teacher came up with such a task that the first derivatives should be given $$$S_ {1} ^ {'} (x_1) = k_1$ and $$$S_ {n-1} ^ {'} (x_n) = k_2$ at the left and right ends of the interval, and the program should read the interpolating curve. And for such a requirement I did not find ready-made algorithms ...
Of course, I will not describe your entire “creative” path from the moment when I heard the task, before I passed it. I will tell only the idea itself and show its implementation.

The difficulty of the task is that, by specifying the first derivatives at the ends of the interval, yes, we are asking this spline. In theory. But to count it in practice is a rather complicated and completely unobvious task (those who wish can see the code for finding a natural spline on the wiki - ru.wikipedia.org/wiki/Kubichesky_spline - and try to understand it at least). Of course, I absolutely did not want to spend a lot of time digging into matan and trying to deduce the formulas I needed. I wanted a simpler and more elegant solution. And I found it.
Consider our spline and take the first of its intervals. There are already 3 conditions on this interval:

$$$S_1 (x_1) = y_1$

$$$S_1 (x_2) = y_2$

$$$S_ {1} ^ {'} (x_1) = k_1$ - set by user

In order to uniquely define a cubic polynomial on this interval, we still lack only one condition. But we can just invent it! Take the second derivative and set it equal, for example, 0:

$$$S_ {1} ^ {''} (x_1) = 0$ - unwarranted assumption

Thus, knowing these 4 conditions, we completely define this polynomial. Knowing all the parameters of this polynomial, we can calculate the values ​​of the first and second derivatives on the second point, and since they coincide with the values ​​of the first and second derivatives for the polynomial on the second interval, this leads to the fact that we also define the second polynomial:

$$$S_2 (x_2) = y_2$

$$$S_2 (x_3) = y_3$

$$$S_ {2} ^ {'} (x_2) = S_ {1} ^ {'} (x_2)$ - calculated from $$$S_1$

$$$S_ {2} ^ {''} (x_2) = S_ {1} ^ {''} (x_2)$ - calculated from $$$S_1$

Similarly, we consider the third polynomial, the fourth, the fifth, and so on, no matter how many. That is, in fact, we recreate the entire spline. But since we took $$$S_ {1} ^ {''} (x_1) = 0$ completely random, this will cause the derivative $$$k_2$ specified by the user at the right end of the spline will not match the derivative $$$S_ {n-1} ^ {'} (x_n)$ , which we got in the course of such calculations. But it turns out that the value of the derivative $$$S_ {n-1} ^ {'} (x_n)$ on the right end of the spline is a function depending on the value of the second derivative $$$S_ {1} ^ {''} (x_1)$ on the left end:

$$$S_ {n-1} ^ {'} (x_n) = f (S_ {1} ^ {' '}} (x_1))$

And since such a spline, which would satisfy the specified conditions, is guaranteed to exist, and exists in a single copy, this means that we can consider the difference:

$$$delta = S_ {n-1} ^ {'} (x_n) -k_2$

and try to find such a value $$$S_ {1} ^ {''} (x_1)$ in which $$$delta$ would turn to 0 - and that would be the correct value $$$S_ {1} ^ {''} (x_1)$ which is built by the user spline:



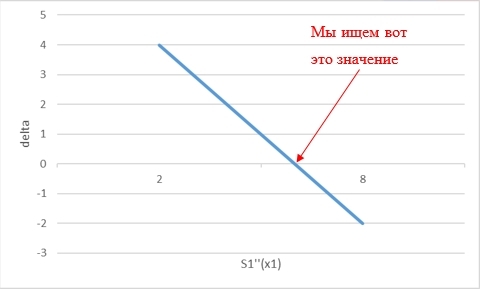
The most remarkable thing in my idea is that this dependence turned out to be linear (regardless of the number of points through which we draw a spline. This fact is proved by theoretical calculations), which means you can randomly take any two initial values $$$S_ {11} ^ {''} (x_1)$ and $$$S_ {12} ^ {''} (x_1)$ count $$$delta_1$ and $$$delta_2$ , and immediately calculate the exact value that the required spline will build for us:

$$$S_ {REAL} ^ {''} (x_1) = - delta_2 \ frac {S_ {12} ^ {''} (x_1) -S_ {11} ^ {''} (x_1)} {delta_2-delta_1}$

Total, we are guaranteed to find the desired spline for 3 runs of such calculations.

Some code and screenshots of the program

class CPoint { public int X { get; } public int Y { get; } public double Df { get; set; } public double Ddf { get; set; } public CPoint(int x, int y) { X = x; Y = y; } } 

 class CSplineSubinterval { public double A { get; } public double B { get; } public double C { get; } public double D { get; } private readonly CPoint _p1; private readonly CPoint _p2; public CSplineSubinterval(CPoint p1, CPoint p2, double df, double ddf) { _p1 = p1; _p2 = p2; B = ddf; C = df; D = p1.Y; A = (_p2.Y - B * Math.Pow(_p2.X - _p1.X, 2) - C * (_p2.X - _p1.X) - D) / Math.Pow(_p2.X - _p1.X, 3); } public double F(int x) { return A * Math.Pow(x - _p1.X, 3) + B * Math.Pow(x - _p1.X, 2) + C * (x - _p1.X) + D; } public double Df(int x) { return 3 * A * Math.Pow(x - _p1.X, 2) + 2 * B * (x - _p1.X) + C; } public double Ddf(int x) { return 6 * A * (x - _p1.X) + 2 * B; } } 

 class CSpline { private readonly CPoint[] _points; private readonly CSplineSubinterval[] _splines; public double Df1 { get { return _points[0].Df; } set { _points[0].Df = value; } } public double Ddf1 { get { return _points[0].Ddf; } set { _points[0].Ddf = value; } } public double Dfn { get { return _points[_points.Length - 1].Df; } set { _points[_points.Length - 1].Df = value; } } public double Ddfn { get { return _points[_points.Length - 1].Ddf; } set { _points[_points.Length - 1].Ddf = value; } } public CSpline(CPoint[] points) { _points = points; _splines = new CSplineSubinterval[points.Length - 1]; } public void GenerateSplines() { const double x1 = 0; var y1 = BuildSplines(x1); const double x2 = 10; var y2 = BuildSplines(x2); _points[0].Ddf = -y1 * (x2 - x1) / (y2 - y1); BuildSplines(_points[0].Ddf); _points[_points.Length - 1].Ddf = _splines[_splines.Length - 1].Ddf(_points[_points.Length - 1].X); } private double BuildSplines(double ddf1) { double df = _points[0].Df, ddf = ddf1; for (var i = 0; i < _splines.Length; i++) { _splines[i] = new CSplineSubinterval(_points[i], _points[i + 1], df, ddf); df = _splines[i].Df(_points[i + 1].X); ddf = _splines[i].Ddf(_points[i + 1].X); if (i < _splines.Length - 1) { _points[i + 1].Df = df; _points[i + 1].Ddf = ddf; } } return df - Dfn; } }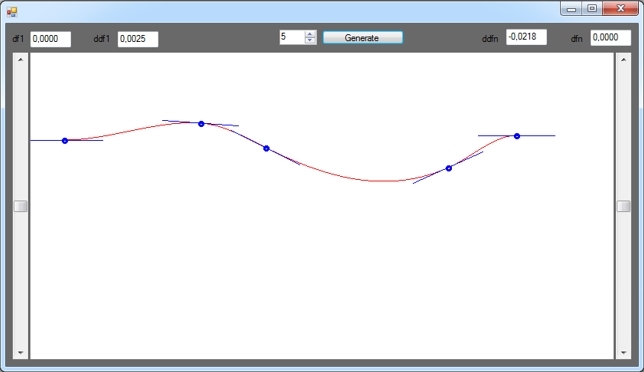 

The blue segments are the first derivatives of the spline at its corresponding points. Added such a graphic element for clarity.

Advantages and disadvantages of the algorithm

Frankly, I did not conduct any serious analysis. It would be good to write tests, check how it works in different conditions (few / many interpolation points, equal / arbitrary between points, linear / square / cubic / trigonometric / etc. Functions, etc.), but I did not , sorry :)

Offhand, we can say that the complexity of the algorithm is O (N), since, as I said, regardless of the number of points, two computation runs are enough to get the right value of the second derivative at the left end of the interval, and another one to build a spline .

However, if someone wants to delve into the code and conduct some more detailed analysis of this algorithm, I will be only too happy. Write me except about the results, I would be interested.

So what were the IQ tests wrong with?

At the very beginning of the article I wrote two numerical series and asked them to continue. This is a fairly frequent question in all IQ tests. In principle, the question is like a question, but if you dig a little deeper, it turns out that it is rather delusional, because with some desire you can prove that there is no “correct” answer to it.

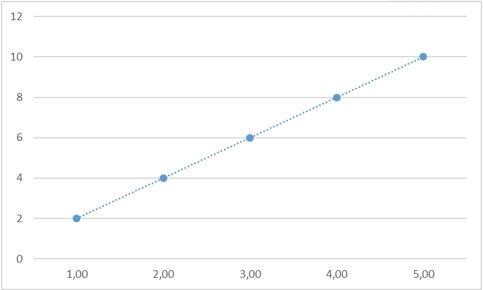
Consider first a series of "2, 4, 6, 8,?"
Imagine this number series as a set of pairs of values $$${x_i, y_i}$ :



where as $$$y_i$ we take the number itself as well as $$$x_i$ - the sequence number of this number. What value should be in place $$$y_5$ ?

The thought to which I try to smoothly lead is that we can substitute absolutely any value. After all, in fact, check such problems? The ability of a person to find some rule that binds all the available numbers, and according to this rule output the next number in the sequence. Speaking in scientific language, there is an extrapolation problem (the interpolation problem is to find a curve passing through all points within a certain interval, and the extrapolation task is to continue this curve outside the interval, “predicting” the behavior of the curve in the future). So, extrapolation does not have a unique solution. At all. Never. If it were otherwise, people would long ago have predicted the weather forecast for the whole history of humanity ahead, and the jumps of the ruble exchange rate would never be a surprise.

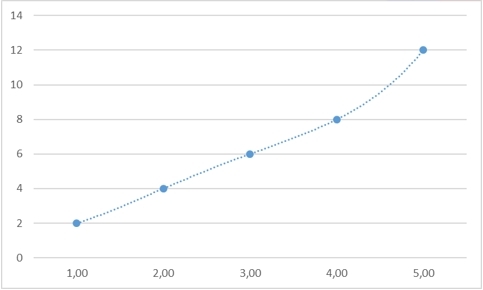
Of course, it is assumed that the correct answer in this problem is still there and it is equal to 10, and then the “law” connecting all these numbers is $$$y = 2x_i$



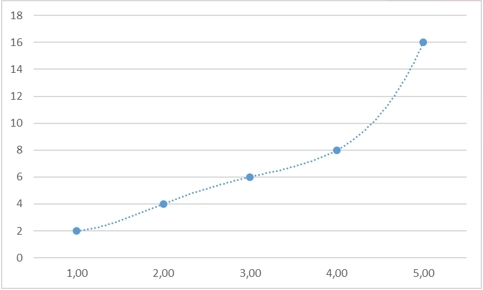
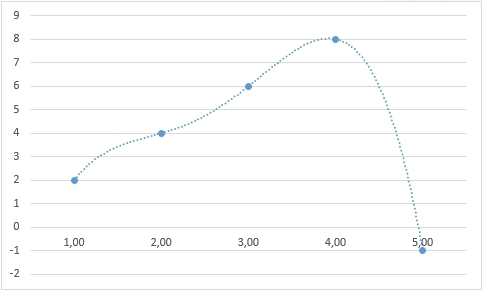
However, we take any other value - and we can also find a law that would justify it:

$$$y_5 = 12 \ to y = \ frac {x ^ 4} {12} - \ frac {5x ^ 3} {6} + \ frac {35x ^ 2} {12} - \ frac {13x} {6} + $$


$$$y_5 = 16 \ to y = \ frac {x ^ 4} {4} - \ frac {5x ^ 3} {2} + \ frac {35x ^ 2} {4} - \ frac {21x} {2} + 6$


$$$y_5 = -1 \ to y = - \ frac {11x ^ 4} {24} + \ frac {55x ^ 3} {12} - \ frac {385x ^ 2} {24} + \ frac {299x} {12 } -11$


Well, they figured out the extrapolation, it does not have a unique solution even theoretically. But maybe we can find the missing number in the second row?



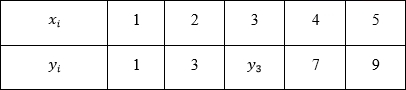
I believe the right answer $$$y_3 = 1$ . Who can challenge? :)

$$$y = -x ^ 4 + 12x ^ 3-49x ^ 2 + 80x-41$

Git repository

Last time, they scolded me for putting the project in the form of an archive in the cloud, and not in the form of codes in the repository, so this time I correct this error: github.com/WieRuindl/Splines