Search space strategies. AI driver
I post a report on my experiment in machine learning. This time the theme of the experiment was the creation of an AI to control the model car.
As written on smart sites , there are two basic ways to have a control object maximize a certain evaluation function:
1) Program training with reinforcements (hello to Pavlov dogs)
2) Conduct a direct search in the strategy space
I decided to choose the second option.
')
AI-driver
As a model problem, I chose a subtask from one championship on AI (when I solved it for the first time, I was not able to machine learning).
There is an object. It can turn right-left and accelerate back and forth (forward - faster, back - slower). What is the fastest way to get this object from point A to point B?

Matlab simulation code
function q = evaluateNN(input,nn) unit.angle=0; unit.x=0; unit.y=0; trg.x=input(1); trg.y=input(2); q=0; rmin=1e100; for i=1:20 % "" 20 % tangle=180*atan2(-unit.y+trg.y,-unit.x+trg.x)/3.141-unit.angle; if(tangle>180) tangle=tangle-360; end; if(tangle<-180) tangle=tangle+360; end; r=sqrt((unit.y-trg.y)^2+(unit.x-trg.x)^2); % answArr=fastSim(nn,[tangle;r]); answArr(1)=(10+(-2))/2+ answArr(1)*(10-(-2))/2; answArr(2)=(30+(-30))/2+ answArr(2)*(30-(-30))/2; % vx=answArr(1)*cos(3.141*unit.angle/180); vy=answArr(1)*sin(3.141*unit.angle/180); unit.x=unit.x+vx; unit.y=unit.y+vy; unit.angle=unit.angle+answArr(2); %, . if(r<rmin) rmin=r; end; end; q=-rmin; if(q>0) q=0; end; end In fact, the problem can be solved by writing down the differential equation of motion and solving it ... But I am not strong in diffuras. Therefore, regularly faced with such problems:
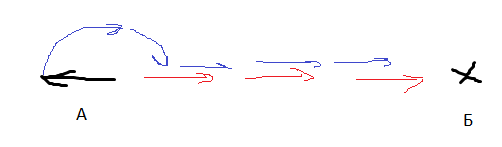
Unit turned back to the target. Is it better for him to turn around and drive, or go in reverse?

Unit turned to the target under 70 degrees. Is it better for me to accelerate and simultaneously turn, or first turn, and then accelerate? How to choose a threshold that separates one strategy from another?
Now, when I have an efficient optimizing algorithm and high-speed neural networks, I solved the problem by searching for strategies. That is, I presented our task as a function, where the input values are weights and shifts of neurons, and the output value is a numerical evaluation of the effectiveness of this strategy (this numerical estimate is called a quality function or a quality metric).
Input network data:
1) Direction to the target (from -180 to 180 degrees)
2) Distance to the target
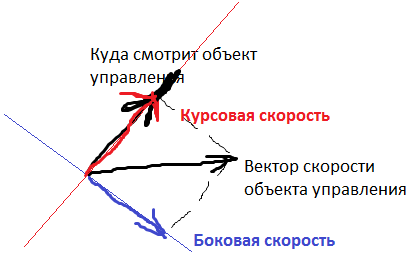
3) Course speed of the control object
4) Lateral speed of the control object
Heading and side speeds are these things:
Output values - the position of the steering wheel (from -30 to +30 degrees per stroke) and acceleration from the engine (from -2 to +10 cells / turn per turn).
As a function of quality in a single test, I chose q = (- the minimum distance to the target). Q is always negative, but the more Q, the higher we evaluate the quality of the algorithm. Since I conduct several tests, it is necessary to derive some uniform quality metric from them.
I took the worst quality value for all tests as a metric - that is, the bot wants to improve not the average, but the worst of the results. I did so that AI did not seek to optimize the results of some tests to the detriment of the results of other tests.
My neural network consisted of 2 layers of 7 neurons each, the activation function of each neuron is arctangent.
A few minutes of training and ...

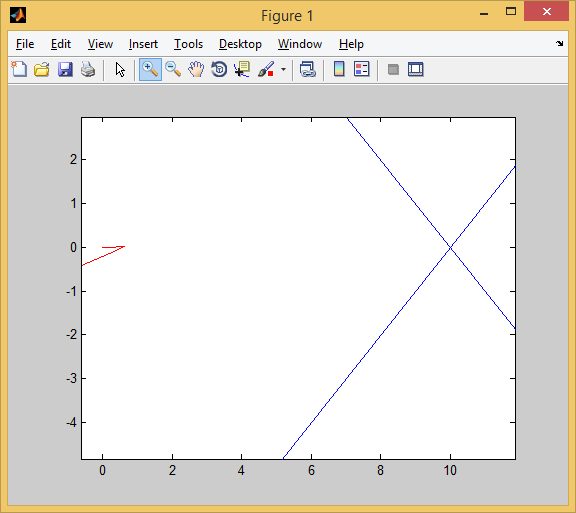
AI began to be aimed at a target like this. The red arrow is the orientation of the car. That is, the bot backed up, simultaneously unfolded, and then moved from reverse to forward. At the same time, he achieved the goal faster than the strategy of “first at least partially turn around, then go” and than the strategy of “go backwards”.
AI-collector
We slightly change the problem statement. All the same plane, all the same opportunities to accelerate / turn (this time the acceleration from -3 to 7, and the rotation from -30 to 30 degrees per turn). Each trial is limited to 100 moves.
But now there are several goals. Each goal is fixed. AI sees them in this way:

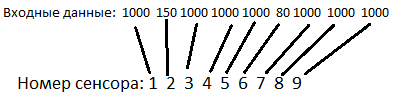
The neural network has a viewing angle of 200 degrees, which is divided into 9 equal sectors (22 degrees each). If a target hits one of the sectors, then a number equal to the distance to the target hits the corresponding sensor of the neural network. If there is no target in the sector, then the number 1000 reaches the sensor (almost all distances in the simulation are less than this number).
If the controlled object approaches the target at a distance of 10 or less, the target is destroyed, and the AI gets 10 points (such as has eaten the target).
The initial coordinates of the control object are zero (0,0). The coordinates of the targets in the first test are:
[50,100] [10,30] [100, -120] [60,75]
These are typical coordinates. All tests 6, and the coordinates of approximately the same order. Goals are always 4.
I put AI on training. AI unsuccessfully tries to learn for several hours. On average, he captures one goal per test (even slightly less). I suppose the problem is that the function of the dependence of the reward on the coefficients is piecewise constant.
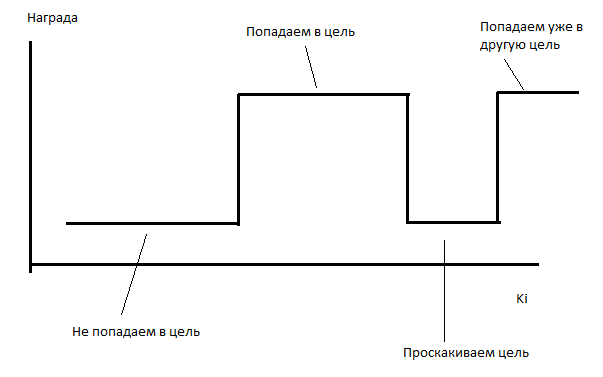
In such cases, my optimizer works rather poorly (and evolution in such cases does not cope much).
Therefore, I do a little cheating. I make each AI move get the number of points inversely proportional to the distance to each of the uncollected targets. He gets 0.1 / r points for each goal. That is, at a distance of 10 he will receive 0.001 points per goal, and “eating” this goal will give 10 points. The number of points obtained by AI varies very little, but the function becomes a piecewise variable, that is, it has a nonzero derivative.
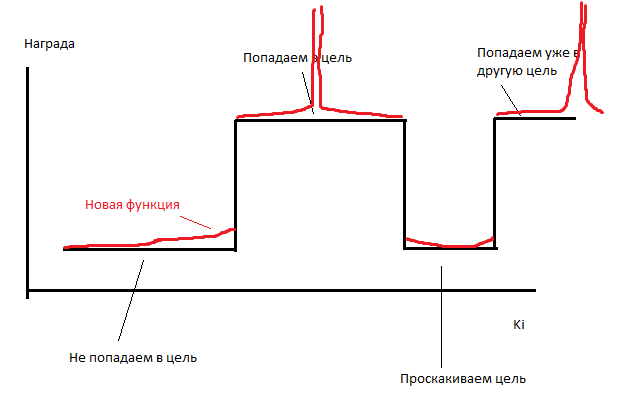
Simulation source code with driver finding key points
function q = evaluateNN(input,nn) unit.angle=0; unit.x=0; unit.y=0; unit.vx=0; unit.vy=0; trg=[]; trg(1).x=input(1); trg(1).y=input(2); trg(1).pickable=1; trg(2).x=input(3); trg(2).y=input(4); trg(2).pickable=1; trg(3).x=input(5); trg(3).y=input(6); trg(3).pickable=1; trg(4).x=input(7); trg(4).y=input(8); trg(4).pickable=1; tsz=size(trg); tangle=[]; r=[]; sensor=[]; sensorMax=5; sensorBound=70; sectorSize=2*sensorBound/sensorMax; q=-100; rmin=1e100; for i=1:200 % for j=1:sensorMax sensor(j)=1e4; end; for j=1:tsz(2) tangle(j)=180*atan2(-unit.y+trg(j).y,-unit.x+trg(j).x)/3.141-unit.angle; if(tangle>180) tangle=tangle-360; end; if(tangle<-180) tangle=tangle+360; end; r(j)=sqrt((unit.y-trg(j).y)^2+(unit.x-trg(j).x)^2); if(tangle(j)>-sensorBound && tangle(j)<sensorBound && trg(j).pickable==1) %target in field of view index=floor((tangle(j)+sensorBound)/sectorSize)+1; if(sensor(index)>r(j)) sensor(index)=r(j); end; end; % if(r(j)<10 && trg(j).pickable==1) %picked up q=q+10; trg(j).pickable=0; end; % if(r(j)<50 && trg(j).pickable==1) q=q+1/r(j); end; end; % : vangle=180*atan2(unit.vy,unit.vx)/3.141; vr=unit.vy*sin(3.141*unit.angle/180)+unit.vx*cos(3.141*unit.angle/180);%v-radial. Scalar multing vb=-unit.vx*sin(3.141*unit.angle/180)+unit.vy*cos(3.141*unit.angle/180);%v-back. vx*(-y)+vy*x % answArr=fastSim(nn,[sensor'';vr;vb]); answArr(1)=(4+(-1))/2+ answArr(1)*(4-(-1))/2; answArr(2)=(30+(-30))/2+ answArr(2)*(30-(-30))/2; % ax=answArr(1)*cos(3.141*unit.angle/180); ay=answArr(1)*sin(3.141*unit.angle/180); unit.vx=unit.vx+ax; unit.vy=unit.vy+ay; unit.x=unit.x+unit.vx; unit.y=unit.y+unit.vy; unit.angle=unit.angle+answArr(2); end; if(q>0) q=0; end; end At the same time, I combined the results of several tests as follows: I took the average result and the worst, and took the average from them.
nnlocal=ktonn(nn,k); arr=[1,2,3,4,1,2,3,4]; input=[[50,100,10,30,100,-120,60,75];[-50,50,-100,100,10,0,20,-90];[100,-60,-100,15,20,0,15,4];[-100,-10,-25,15,60,-5,-80,10];[-10,-70,0,-40,0,40,20,22]; [20,-100,-20,22,-30,0,100,-10];]; for (i=1:6) nncopy=nnlocal; val=evaluateNN(input(i,:),nncopy); sum_=sum_+val; arr(i)=val; countOfPoints=countOfPoints+1; end; q=sum_/countOfPoints- sum(abs(k))*0.00001; The work went more cheerful. A few tens of minutes - and voila:
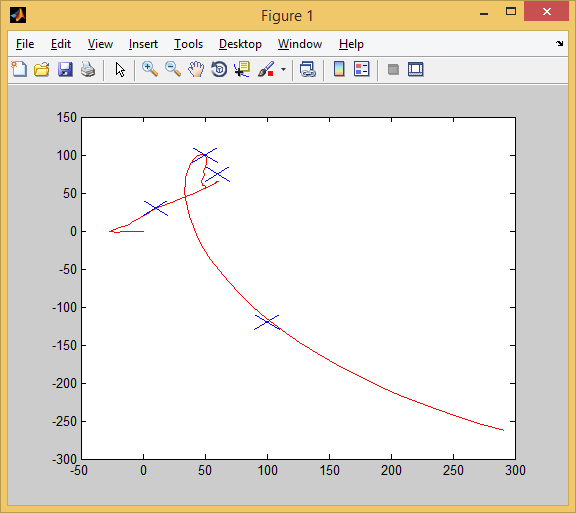
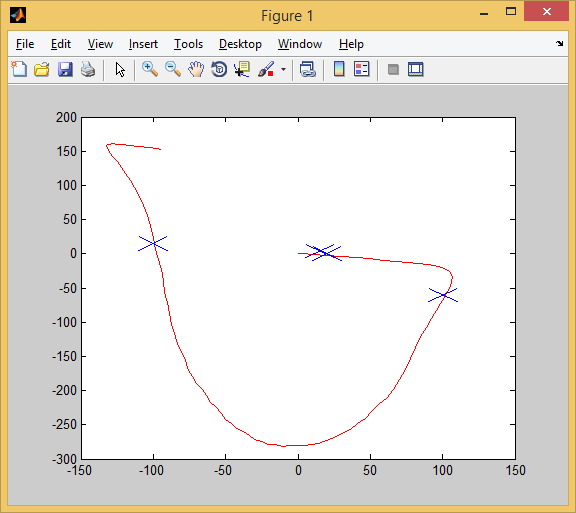
So we pass the first test. All targets (blue crosses) successfully captured.
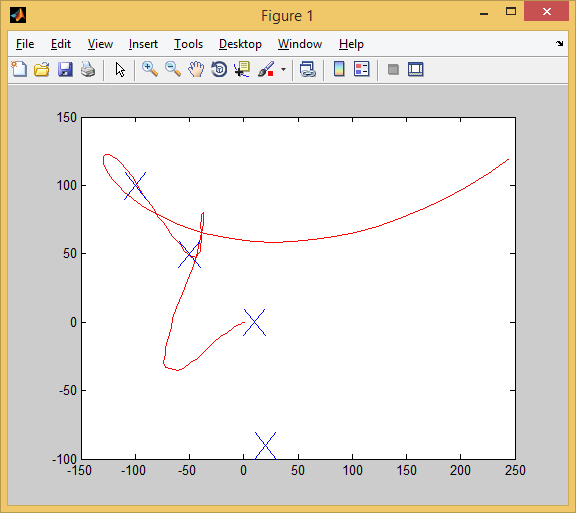
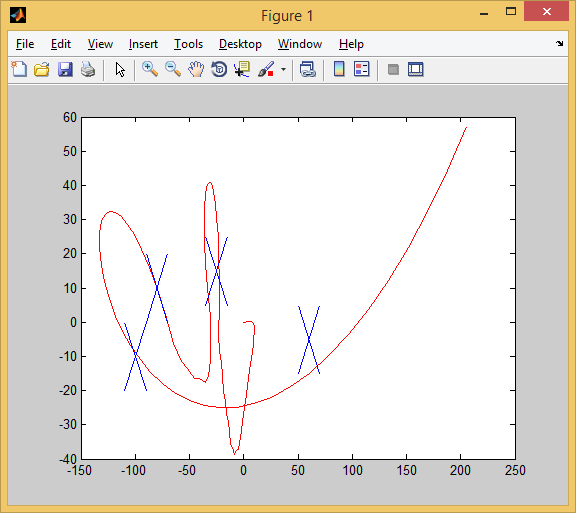
So we pass the second test. Three targets were captured (in order to capture that first target, we had to drive forward a little and then turn around. It looks like this in close-up:
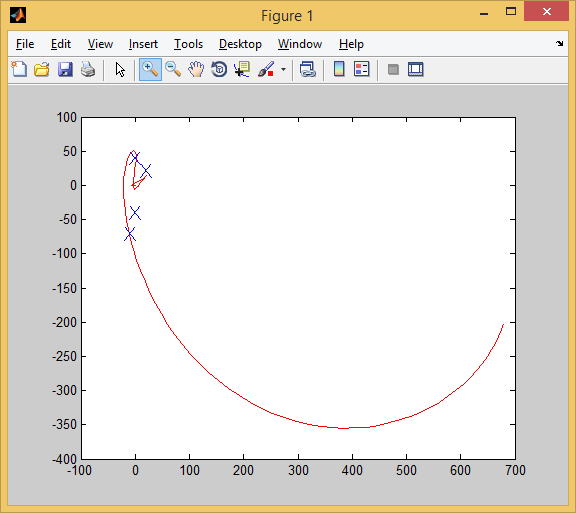
In the 3rd trial, too, 4 out of 4:
And in the 4th:
And in the 5th:
But in the 6th we already have 3 out of 4.

Now we will set new tests - those that were not in the training set (we will cross-test).

3 out of 4! Frankly, I doubted to the last that AI could transfer the experience of the training sample to the test one.
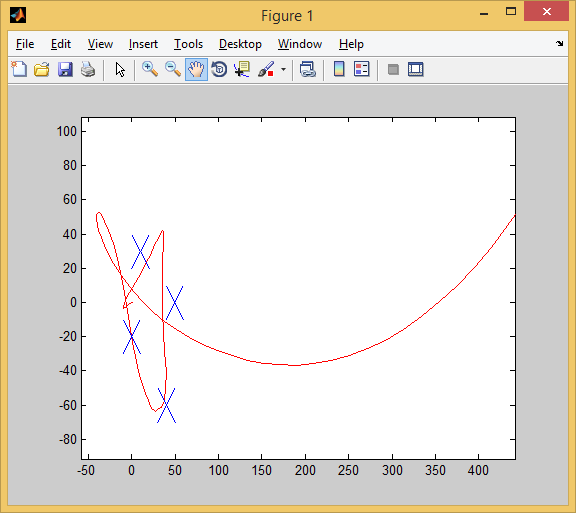
I worked 3 goals, and missed a little past one.
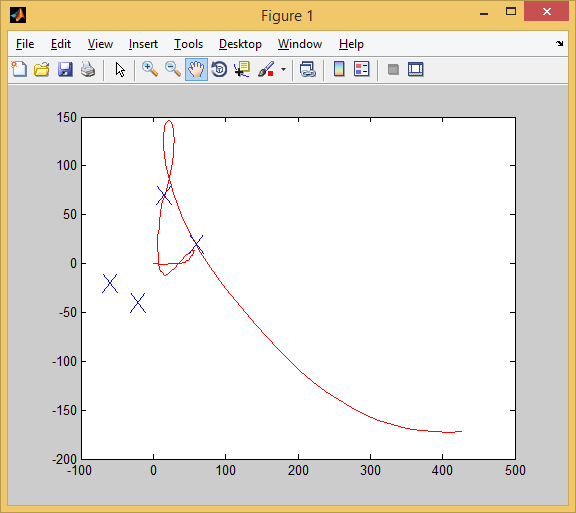
Well, here AI completely screwed up. Worked 2 goals out of 4.
Conclusion
The report of the experiment should end with conclusions. The conclusions are as follows:
1) Learning by iterating strategy space is a promising technique. But it is demanding of the optimizer - I used a rather confused algorithm for selecting parameters.
2) A piecewise constant quality function is evil. If a function does not have something that even remotely resembles a derivative, it will be very difficult to optimize it.
3) 2 layers of 7 neurons - this is enough to make a simple autopilot. Usually 14 neurons is a puff from which no useful function can be assembled.
I would be grateful for the comments, comrades!
If I like the article, I will tell you how I did a similar AI for a game like Mortal Kombat.
Source: https://habr.com/ru/post/323424/
All Articles