RandLib. Library of probability distributions in C ++ 17
The RandLib library allows you to work with more than 50 known distributions, continuous, discrete, two-dimensional, cyclic, and even one singular. If you need any distribution, then enter its name and add the Rand suffix. Interested?
Random Variables
If we want to generate a million random variables from a normal distribution using the standard C ++ template library, we will write something like
std::random_device rd; std::mt19937 gen(rd()); std::normal_distribution<> X(0, 1); std::vector<double> data(1e6); for (double &var : data) var = X(gen); Six intuitive not very clear lines. RandLib allows you to halve their number.
NormalRand X(0, 1); std::vector<double> data(1e6); X.Sample(data); If you need only one random standard normally distributed value, then this can be done in one line
')
double var = NormalRand::StandardVariate(); As you can see, RandLib eliminates the user from two things: choosing a basic generator (a function that returns an integer from 0 to some RAND_MAX) and choosing a starting position for a random sequence (srand () function). This is done in the name of convenience, since this choice is most likely to no use to many users. In the overwhelming majority of cases, random variables are not generated directly through the basic generator, but through a random variable U, uniformly distributed from 0 to 1, which already depends on this basic generator. In order to change the way U is generated, the following directives should be used:
#define UNIDBLRAND // #define JLKISS64RAND // 64- #define UNICLOSEDRAND // U 0 1 #define UNIHALFCLOSEDRAND // U 0, 1 By default, U returns neither 0 nor 1.
Generation rate
The following table provides a comparison of the time to generate one random variable in microseconds.
System characteristics
Ubuntu 16.04 LTS
Processor: Intel Core i7-4710MQ CPU @ 2.50GHz × 8
OS type: 64-bit
Processor: Intel Core i7-4710MQ CPU @ 2.50GHz × 8
OS type: 64-bit
| Distribution | STL | RandLib |
|---|---|---|
| 0.017 μs | 0.006 μs | |
| 0.075 μs | 0.018 μs | |
| 0.109 μs | 0.016 μs | |
| 0.122 μs | 0.024 μs | |
| 0.158 μs | 0.101 μs | |
| 0.108 μs | 0.019 μs |
More comparisons
| Gamma distribution: | ||
|---|---|---|
| 0.207 μs | 0.09 μs | |
| 0.161 μs | 0.016 μs | |
| 0.159 μs | 0.032 μs | |
| 0.159 μs | 0.03 μs | |
| 0.159 μs | 0.082 μs | |
| Student's distribution: | ||
| 0.248 μs | 0.107 μs | |
| 0.262 μs | 0.024 μs | |
| 0.33 μs | 0.107 μs | |
| 0.236 μs | 0.039 μs | |
| 0.233 μs | 0.108 μs | |
| Fisher distribution: | ||
| 0.361 μs | 0.099 μs | |
| 0.319 μs | 0.013 μs | |
| 0.314 μs | 0.027 μs | |
| 0.331 μs | 0.169 μs | |
| 0.333 μs | 0.177 μs | |
| Binomial distribution: | ||
| 0.655 μs | 0.033 μs | |
| 0.444 μs | 0.093 μs | |
| 0.873 μs | 0.197 μs | |
| Poisson distribution: | ||
| 0.048 μs | 0.015 μs | |
| 0.446 μs | 0.105 μs | |
| Negative binomial distribution: | ||
| 0.297 μs | 0.019 μs | |
| 0.587 μs | 0.257 μs | |
| 1.017 μs | 0.108 μs |
As you can see, RandLib is sometimes 1.5 times faster than STL, sometimes 2, sometimes 10, but never slower. Examples of algorithms implemented in RandLib can be found here and here .
Distribution functions, moments, and other properties
In addition to generators, RandLib provides the ability to calculate probability functions for any of these distributions. For example, to find out the probability that a random variable with a Poisson distribution with the parameter a takes the value k, you must call the function P.
int a = 5, k = 1; PoissonRand X(a); XP(k); // 0.0336897 It so happened that the capital letter P denotes a function that returns the probability of accepting any value for a discrete distribution. For continuous distributions, this probability is zero almost everywhere, so density is considered instead, which is denoted by the letter f. In order to calculate the distribution function, for both continuous and discrete distributions, you need to call the function F:
double x = 0; NormalRand X(0, 1); Xf(x); // 0.398942 XF(x); // 0 Sometimes you need to calculate the function 1-F (x), where F (x) takes very small values. In such a case, in order not to lose accuracy, the function S (x) should be called.
If you need to calculate probabilities for a whole set of values, then for this you need to call functions:
//x y - std::vector X.CumulativeDistributionFunction(x, y); // y = F(x) X.SurvivalFunction(x, y); // y = S(x) X.ProbabilityDensityFunction(x, y) // y = f(x) - X.ProbabilityMassFunction(x, y) // y = P(x) - A quantile is a function of p that returns x, such that p = F (x). Corresponding implementations are also in each final RandLib class corresponding to a one-dimensional distribution:
X.Quantile(p); // x = F^(-1)(p) X.Quantile1m(p); // x = S^(-1)(p) X.QuantileFunction(x, y) // y = F^(-1)(x) X.QuantileFunction1m(x, y) // y = S^(-1)(x) Sometimes, instead of the functions f (x) or P (k), it is necessary to obtain the corresponding logarithms. In this case, it is best to use the following functions:
X.logf(k); // x = log(f(k)) X.logP(k); // x = log(P(k)) X.LogProbabilityDensityFunction(x, y) // y = logf(x) - X.LogProbabilityMassFunction(x, y) // y = logP(x) - RandLib also provides the ability to calculate the characteristic function:
X.CF(t); // \phi(t) X.CharacteristicFunction(x, y) // y = \phi(x) In addition, you can easily get the first four points or the expectation, variance, coefficients of asymmetry and kurtosis. In addition, the median (F ^ (- 1) (0.5)) and mode (the point where f or P takes the greatest value).
LogNormalRand X(1, 1); std::cout << " Mean = " << X.Mean() << " and Variance = " << X.Variance() << "\n Median = " << X.Median() << " and Mode = " << X.Mode() << "\n Skewness = " << X.Skewness() << " and Excess kurtosis = " << X.ExcessKurtosis(); 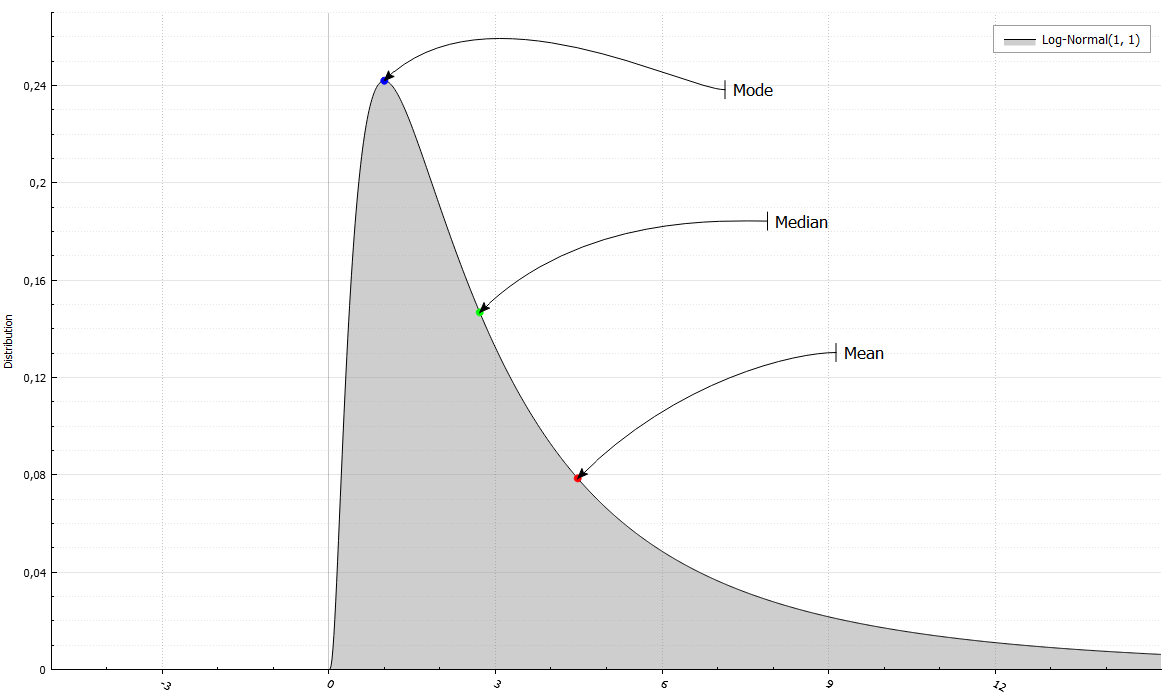
Mean = 4.48169 and Variance = 34.5126 Median = 2.71828 and Mode = 1 Skewness = 6.18488 and Excess Kurtosis = 110.936 Parameter Estimates and Statistical Tests
From probability theory to statistics. For some (not yet all) classes, there is a Fit function, which sets the parameters corresponding to a certain estimate. Consider the example of a normal distribution:
using std::cout; NormalRand X(0, 1); std::vector<double> data(10); X.Sample(data); cout << "True distribution: " << X.Name() << "\n"; cout << "Sample: "; for (double var : data) cout << var << " "; We generated 10 elements from the standard normal distribution. At the exit should get something like:
True distribution: Normal(0, 1) Sample: -0.328154 0.709122 -0.607214 1.11472 -1.23726 -0.123584 0.59374 -1.20573 -0.397376 -1.63173 The Fit function in this case will set the parameters corresponding to the maximum likelihood estimate:
X.Fit(data); cout << "Maximum-likelihood estimator: " << X.Name(); // Normal(-0.3113, 0.7425) As is known, the maximum likelihood for the dispersion of the normal distribution gives a biased estimate. Therefore, the Fit function has an additional unbiased parameter (false by default) that can be used to adjust the bias / non-bias of the estimate.
X.Fit(data, true); cout << "UMVU estimator: " << X.Name(); // Normal(-0.3113, 0.825) For lovers of Bayesian ideology, there is also a Bayesian assessment. The RandLib structure makes it very convenient to operate with a priori and a posteriori distributions:
NormalInverseGammaRand prior(0, 1, 1, 1); NormalInverseGammaRand posterior = X.FitBayes(data, prior); cout << "Bayesian estimator: " << X.Name(); // Normal(-0.2830, 0.9513) cout << "(Posterior distribution: " << posterior.Name() << ")"; // Normal-Inverse-Gamma(-0.2830, 11, 6, 4.756) Tests
How do I know that generators, like distribution functions, return the correct values? Answer: compare one with the other. For continuous distributions, a function is implemented that carries out a Kolmogorov-Smirnov test for the belonging of this sample to an appropriate distribution. The KolmogorovSmirnovTest function accepts ordinal statistics and the \ alpha level as input, and returns true if the sample corresponds to the distribution. Discrete distributions correspond to the PearsonChiSquaredTest function.
Conclusion
This article is specially written for the part of the social community interested in the similar and able to evaluate. Understand, poke, use to health. Main advantages:
- Free
- Open source
- Work speed
- Convenience of use (my subjective opinion)
- No dependencies (yes, nothing is needed)
Link to release .
Source: https://habr.com/ru/post/323158/
All Articles