Myths about the CAP theorem

Introduction

I have long wanted to write about the myths about the CAP theorem, but somehow everyone did not reach out. However, after reading another opus , I grabbed my head and decided to sort it all out so that a slender picture appeared in my brain.

An event when an article causes a storm of emotions is extremely rare. The first time this happened when I read about chained replication. They tried to convince me that this is a powerful approach and that this is the best thing that could happen with consistent replication. I’ll not argue now why this is not working well, but I’ll just give a talking quotation from the article Chain Replication metadata management :

Split brain management is a thorny problem. The method presented here is one based on pragmatics. If it doesn’t work, it’s not a serious worry. If you end up falling back then “use Riak Ensemble” or “use ZooKeeper”, then perhaps that's fine enough.

In my free retelling, this means something like the following: "We have a certain algorithm here. We do not know whether it will work correctly or not. Yes, it doesn’t matter to us." At least honestly, saved a lot of time, thanks to the authors.

And here, then, comes across an article: Spanner, TrueTime & The CAP Theorem . We will sort it out towards the end, armed with concepts and knowledge. And before that we analyze the most common myths associated with the CAP theorem.

Myth 1: A means accessibility.

A, of course, comes from the word Availability, which means accessibility. But what is accessibility? What kind of?

Accessibility in different contexts means different. And here we must distinguish at least 2 different contexts in which it is used:

1. Availability of real service. This availability is expressed as a percentage: the total downtime during the year is measured and a ratio is compiled, expressed as a percentage, indicating the probability of availability over a long time.
2. Accessibility as part of the CAP theorem model.

The CAP theorem uses the concept that is closest in meaning to the term total availability:

The system should be followed up.

Which means something like the following: "any non-fallen node in the system must respond to the request." There are several points in this definition that I would like to emphasize:

1. "Neupavshaya". It is clear that the fallen node can not answer. However, the catch is that if all the nodes have fallen, then from the point of view of the definition such service is available. In principle, the definition can be corrected by adding to the fact that the client should receive an answer.
2. "Must answer." The theorem does not say exactly when. She is not interested in time parameters at all. It is clear that the node can not respond instantly. And if it cannot, then it is enough that it once answered.

From the user's point of view, if we had 100 nodes and 99 fell, and the remaining one continues to respond at a rate of one request per hour, then such a service can hardly be called accessible (this is context 1). However, from the point of view of the CAP theorem, everything is normal here and such a system will be accessible (context 2).

Therefore, A is not accessibility in the generally accepted sense, but the so-called full accessibility , which the user may be completely uninteresting.

Myth 2: P stands for network separation resistance.

Such a definition can be found in almost all articles. To understand what is wrong here, you need to look at the problem from a different angle.

Take any system that exchanges messages. Consider how messages are transmitted between the actors - the objects of the system. These messages can either reach another actor or not. And here it is necessary to distinguish 2 cases:

1. In the system, the situation when messages are lost is impossible.
2. In the system, it is possible that messages are lost.

It is not difficult to guess that this list is exhaustive. In this place it is worth paying attention that each item describes the properties of the system. Those. we haven't even gotten to the algorithm yet. This will have far-reaching consequences.

If we consider the first case, when messages are never lost, it means that in such a situation network split is simply impossible. Indeed, since each message from each actor can reach without loss, there is no point in talking about network sharing . In the second case, the opposite is true: due to losses, a situation is possible when a whole segment is separated from another, i.e. there was a loss of connectivity between the group of actors. In this case, it is said that network sharing has happened.

It should be noted that the property of the possibility of isolation of groups of actors from each other is a direct consequence of the implementation of paragraph 2.

If we work with a real network, then, as it is not difficult to guess, falls under the 2nd item. At the same time, we have not yet begun to think about the algorithm, and we already have the ability to separate and lose connectivity between groups of actors. P - about this, that splitting is possible in the system. And this is not a property of the algorithm, but a property of the system in which the algorithm operates.

Why, in general, in the case of the loss of messages is it important to consider the network division ? Because the rest of the problems do not cause so much trouble and problems as the splitting of the system into independent parts.

To conclude this myth, I will quote from the blog Aphyr: Percona XtraDB Cluster :

Partition tolerance doesn’t require available to handle requests. It just means that partitions may occur. If you deploy on a typical IP network, partitions will occur; partition tolerance in these environments is not optional.

Thus, if we consider a system that works with a real unreliable network, then network connectivity violations are not an exceptional situation, but something to deal with. And the letter P in this context only means that the system may have a network connectivity violation.

Myth 3: AC systems do not exist

From the previous myth, there may be a feeling that AC systems do not exist, because there are no reliable networks capable of transmitting data. You can immediately try to offer a scheme with redundancy components. However, if the probability of packet loss in a line is> 0, then no matter how we add channels, the probability cannot become = 0 purely from mathematical considerations. And if so, then, as described above, there may be network split (network split).

But who said that CAP only describes network-connected systems? CAP is a theoretical model that can be applied to a very wide class of problems. For example, you can take a multi-core processor:

1. Each core is a separate actor.
2. Actors (kernels) exchange messages (information).

This is enough to talk about the CAP theorem.

Let's first discuss A. Are there kernels available? Of course, yes, at any point in time, you can access any kernel and retrieve any data we want from memory.

What about P? The processor ensures that the data will be transferred without problems to another kernel if necessary. If this for some reason does not happen, then this processor is considered defective. Thus, the letter P is absent.

The issue with consistency is also solved as follows. The memory model is defined by sequential consistency , which is the highest level of consistency in such a system. At the same time, inside the processor, as a rule, cache coherence protocols like MESI or MOESI are implemented, thus ensuring a given level of consistency.

Thus, a modern processor is an AC system with guaranteed message delivery between cores.

Myth 4: C stands for consistency.

C no doubt means consistency. However, what consistency? After all, eventual consistency is also consistency, only extremely weak. So what is meant here? There are a lot of consistency models, just look at the diagram from the article Consistency in Non-Transactional Distributed Storage Systems :

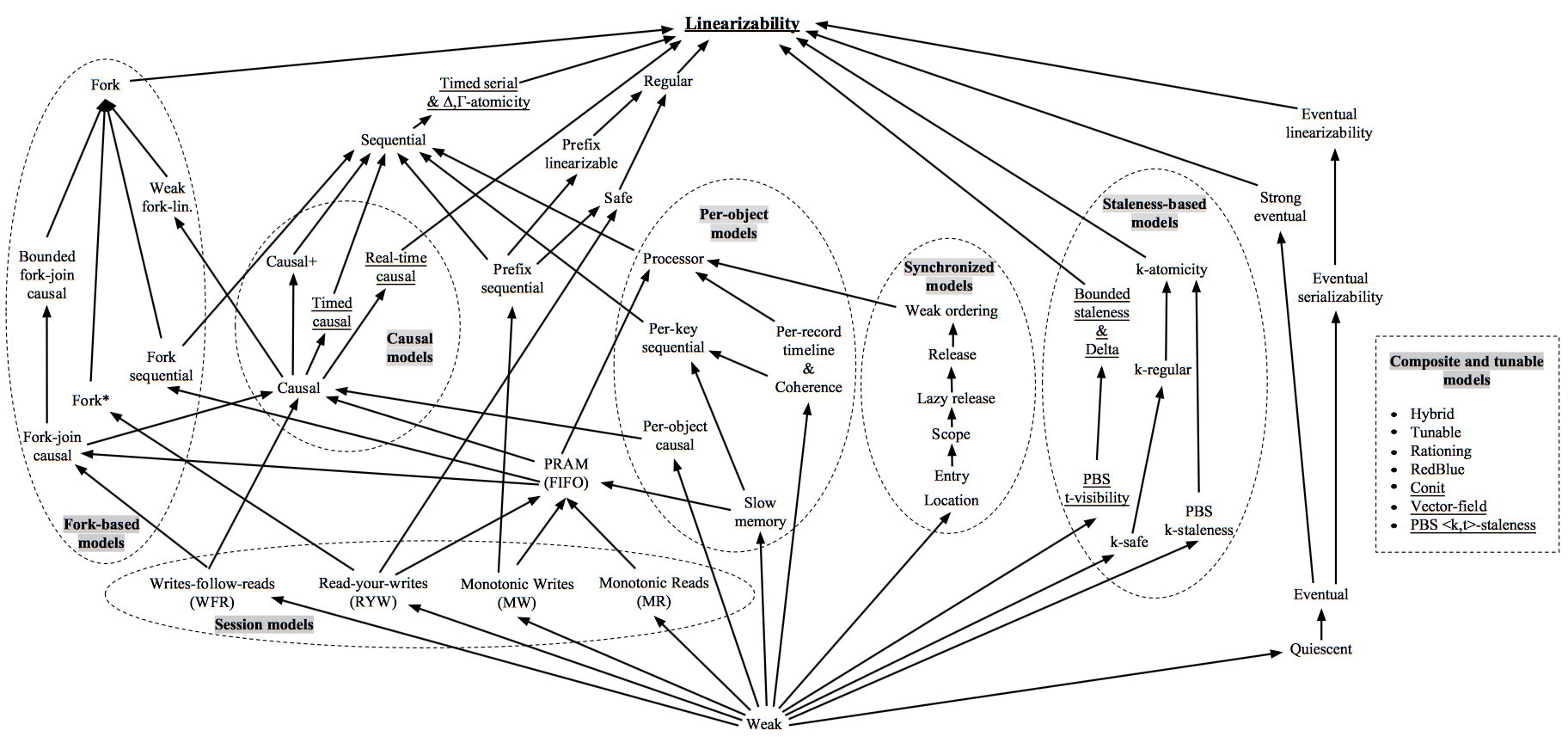
And this is only about distributed non-transactional systems! If we add transactionality to our consideration , we can immediately bury the idea of ​​sorting this out without ever starting.

In the original article about the CAP theorem, we talked everywhere about linearizability. The essence of linearizability, in short, is as follows. If an action has taken place (not important, reading, writing, or a mixed action or actions), the result of this action is available immediately after we receive the answer.

A natural question arises: what about other consistency models? Do they fall under the CAP theorem?

And here begins a complete mess in their heads. Some people think that since the model is proven to be linearizable, then it should be applied strictly and exclusively to linearizability. Others think that any weaker consistency model no longer falls under this theorem. Still others do not understand the essence of the discussion.

To answer this question, consider a wonderful picture taken from the article Highly Available Transactions :

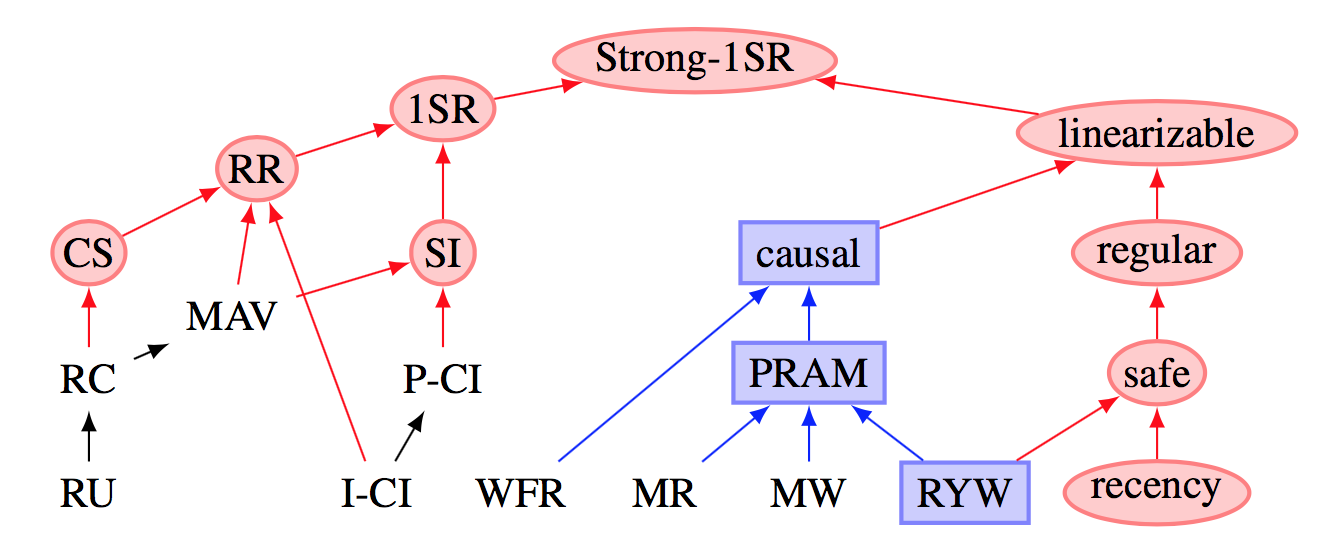
What is she talking about? Red marks the so-called unavailability models that work within the framework of the CAP theorem. Those. simultaneously with it it is impossible to reach A and P simultaneously. However, there are other models that have a sufficient level of consistency for a number of tasks that can nevertheless be executed simultaneously with the AP, receiving the CAP system without any discounts. A typical example: Read Committed (RC) and Monotonic Atomic View (MAV) admit that all three letters in the CAP are respected at the same time, and it is difficult to call such models inconsistent. Such consistency models for which the CAP-theorem is violated are called highly available models.

Thus, speaking of consistency, we mean a wide group of consistency models, called unavailable models .

Myth 5: CP systems are not highly available.

After the previous paragraph, this statement seems quite logical, but fundamentally wrong. Let me remind you that A means complete accessibility, not accessibility within nines. Is it possible to make a CP system highly available?

Here it is necessary to separate the model and iron, i.e. theory and reality.

Let's reason first in the framework of the model. Accessibility within the framework of the CAP theorem means complete availability, i.e. Any live node must respond. But why do you need this at all? After all, the logic of the client, we can write a completely different way. Suppose that we have 3 nodes located in different data centers. We write on a quorum of 2 nodes, while 1 node can lie down without losing the vitality and consistency of the entire system. And we always read from 2 any nodes. Moreover, if one node is lying down, the other node will give the correct answer. If 2 different answers come, we can choose the most recent one. Thus, if in this system it is guaranteed that only one node can be inoperative at any time, then from the client’s point of view, the system will be fully 100% available for both reading and writing. And consistently.

In reality, there is always a non-zero probability that two or more nodes will lie down not one. This is easy to see, because if there is a non-zero probability of falling one node, then there will be a non-zero probability of falling another node or node. Moreover, a fall is not the worst thing that can happen. In addition to equipment failures, there may still be a loss of connectivity, i.e. breakdown of various network equipment, including trunk equipment. I think it is not worth reminding that all this has a non-zero probability. All these probabilities add up, giving only a certain, sometimes very small number of nines. It is clear that the greater the redundancy of nodes, the greater the number of nines can be obtained. And this I have not yet taken into consideration the program itself, which programmers write with a non-zero probability of introducing an error ...

Those. in theory, we have that a correctly written client can achieve 100% availability, but in practice we always have a smaller number. All science is to achieve as many nines as possible. And in this aspect, the CAP theorem is completely useless. Because it is generally about something else.

Therefore, the idea of ​​high availability does not in the least contradict the fact that it is not A, which means that CP can be highly accessible.

Myth 6: CP systems have low performance, high latency, and poorly scaled.

Obviously, the higher the consistency, the less productive the system. The question arises in how much will be a drawdown in performance and whether it will be critical for our processes.

It turns out that even strict consistency or Strong-1SR (the highest level of consistency) can be used in real-time systems. I have experimental evidence of this fact, but here I will give a number of some practical arguments in favor of it.

The idea is to use multiple independent fault tolerant entities. They can be run anywhere, they work in parallel, and their number is actually limited by the size of the cluster. A transactional layer is created on top of these entities, which binds the work of these entities together. This is how Spanner and many other systems work. Thus, scalability and speed are achieved.

Myth 7: AP systems are easy to use because they scale well.

Systems with AP allow simpler scaling, but only in theory. In reality, all the same, one way or another, one has to solve issues of consistency. Practice shows that to write client code based on such a system is an extremely nontrivial task, and sometimes even unattainable. The reason is that if the system does not provide any basic guarantees for consistent data storage, then the subsequent processing turns into a very exciting charade: did the operation apply? Will users see it? and what will they see? Is it possible to get a consistent data slice? will different clients see the same data set? etc.

Those. in spite of the relative simplicity of creating such systems, the complexity of its use increases many times.

Parsing the article

Well, now let's proceed to the analysis of the article Spanner, TrueTime & The CAP Theorem . Let's start from the beginning:

The CAP theorem [Bre12] says:

• C: Consistency, serializability for this discussion;
• A: 100% availability, for both reads and updates;
• P: tolerance to network partitions.

The first thing you should pay attention to is the link [Bre12] called CAP Twelve Years Later , dated May 2012. Why did you choose a link not to the original article - I do not know. Moreover, this is an article about the discussion of the CAP theorem, and not about the derivation of the theorem itself.

About the letters C, A and P, we have already discussed, I will not stop. Further:

Once you’re not sure, you’re willing to use it.

The first part sounds quite reasonable in our discussions, however, after AP & CP is strange, because suddenly it turns out we don’t want to make that choice. Why we do not want to make such a choice, the article is not written. But then the correct words were written:

This is a 100% availability.

It would seem that one could stop at that and say that Spanner is a CP system with an availability of 99.9 ...%, putting an end to this. But no, the author continues to carry and he writes the subtitle:

Spanner claims to be consistent and available.

There are no partitions and are skeptical.

As I showed above, the so-called high availability (highly available) does not mean A at all, much less the absence of P. After this, the verbal balancing act begins, since From an erroneous message, you can derive a lot of funny judgments. The author really wants the system to be both C and A at the same time, because the user doesn’t need a word at all from P. This introduces a new concept: effectively CA. It seems that the author began to play with the concepts and began to invent new ones without any definition, since old ones poorly described such a wonderful system.

We read further:

This is a large number of internal users.

The phrase itself is wonderful. It turns out that if internal users say: "we assume that it is highly accessible", then something immediately follows from here about the system itself. Well, if users had said: "Yes, it is highly accessible," then there is generally something that they only suggest.

This is followed by the enchanting:

If you are not a part of a spanner, then it is more accurate.

Those. if we have a failure that is not related to the violation of network connectivity, then such a system is more precisely in a certain sense (!) should be called as CA. Those. if the probability of other failures is greater than a violation of connectivity, then P is not. In this sense, should understand this phrase?

The following are the marketing speculations that we have built a super-reliable system, supported by graphs. Just below is the definition that finally reveals the meaning of the totality of the word effectively CA :

... to claim this condition of relative probabilities:

1. It can be
2. It is also a small fraction of those outages due to partitions.

Spanner meets both.

Those. the system should:

1. to have high availability in practice, and users can ignore exceptions, and
2. the probability of network separation should be less than other problems.

The question immediately arises: what level of high availability is sufficient in practice? 5 nines? 6 nines? Or maybe all 9? Here we see some arbitrariness, which does not allow one to judge unequivocally about belonging to this property. Well, the "user ignoring exceptions" completes all the ambiguity and ambiguity of this, scary to say, definition.

As can be seen, such a definition does not fall under the model, which is used directly in the CAP theorem. There is generally not clear to which model this applies. It is rather about experimental observations, and not about a theoretical model. And the relationship between experiment and theory in the article can not be traced.

I will not be long to paint other aspects of the article. Let me just say that a number of paragraphs deserve to read them, for example, "What happens during a Partition".

Authors finish with the following magnificent passage:

Spanner’s claim is that it’s always consistent and achieves greater than 5 9s availability.

Well, yes, if we determine that our system is X, then our system will have the properties of X. Great, right? Only this definition has nothing to do with the CAP theorem. This must be clearly understood. The authors, apparently, really wanted to avoid P, but there were 2 other letters, since the user pays for them. Why they did not suit the CP with high availability - I do not know.

Even then outages will occur, in which case Spanner chooses consistency over availability.

What clearly contradicts the CA system: no choice is made in such a system, since both properties are selected, as we saw above in the CA example. The presence of such a statement says just that it is definitely not a CA. I did not expect to see mutually exclusive paragraphs in such an article.

Myth of the last: CAP theorem is outdated

The popularity of this topic led to the fact that many people no longer understand the meaning of the terms, they began to blur, emasculated to a completely vulgar understanding. Speculation on terms, redefinition and misunderstanding - this is an incomplete list of generic spots of this long-suffering theorem.

In the wake of its popularity, the pendulum swung to the other side, and they began to forget a little about this theorem. Articles began to appear about the fact that, say, the CAP theorem is outdated and asked to stop its use . Others tried to criticize and contribute to the instillation and alteration of meanings. Even the author of the theorem begins to replace concepts and distort the original idea.

Such attacks in the direction of the theorem again and again only emphasize its relevance, exposing new, hitherto unknown, faces.

Conclusion

At one time, familiarity with the CAP theorem sober enough brains. After all, the theoretical impossibility of creating a certain type of system provided grounds for not practicing the solution of unsolvable tasks in practice and concentrating on solving problems of a particular class. In the context of distributed systems, it makes sense to talk only about the tasks of an AP or CP.

Such theorems do not become obsolete, as classical mechanics cannot become obsolete, despite the presence of relativistic effects or quantum mechanics. She just needs to find her worthy place, we must remember about her and move on. And the whole point is that this theorem is only a special case of a more general fundamental property :

It is a simple fact that you can achieve a system of unreliable distributed system.

Those. The CAP theorem is simply one example of the fundamental fact that it is impossible to achieve both security and survivability in an unreliable distributed system.

• C: Security
• A: Vitality
• P: Unreliable Distributed System

Grigory Demchenko, developer of YT