Reduction with the use of "regulators": the task of satisfiability
Hi, Habrozhiteli! We decided to publish an excerpt from the book Algorithms: Design and Application. Classic Computers Science. SAT and 3-SAT tasks . Suppose there is a set X of n Boolean variables x1, ..., xn; each variable can take the value 0 or 1 (equivalent to false and true). A literal in X is one of the variables xi or its negation. Finally, a condition is an ordinary literal disjunction. 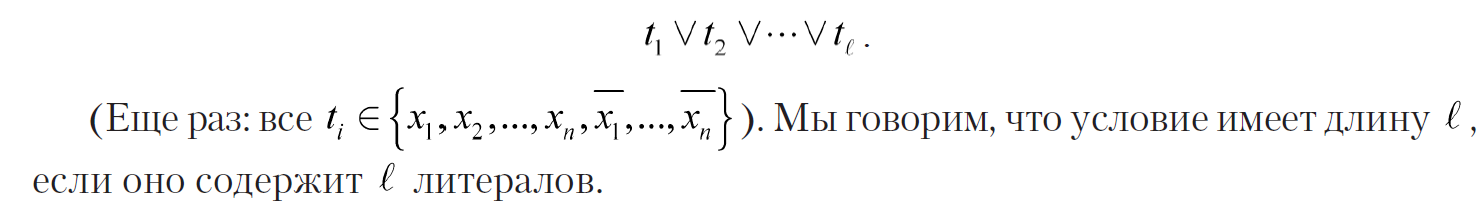
And now we give a formal definition of assigning values satisfying a set of conditions. The logical assignment for X is the assignment of a value of 0 or 1 to each xi; in other words, it is a function ν: X → {0,1}. The assignment of v implicitly sets the truth value, the opposite of xi. An assignment satisfies condition C if after it C gives a result of 1 according to the conditions of Boolean logic; this is equivalent to the requirement that at least one of the literals in C has the value 1. The assignment fulfills the set of conditions C1, ..., Ck if, as a result, its all Ci give the result 1; in other words, if as a result of its conjunction

The logical assignment of ν, which sets the value of 1 to all three variables, is not fulfilling, because the second of the listed conditions is not fulfilled with it; on the other hand, the assignment of ν ', which sets all variables to 0, is fulfilling.
Now we can give the formulation of the problem of feasibility, also denoted by SAT:
For a given set of conditions C1, ..., Ck with respect to the set of variables X = {x1, ..., xn}, does a performing logical assignment exist?
There is a special case of SAT, which has equivalent complexity, but is more understandable; in it all conditions contain exactly three literals (corresponding to different variables). Let's call this task a 3-satisfiability problem, or 3-SAT:
')
For a given set of conditions C1, ..., Ck, each of which has a length of 3, in the set of variables X = {x1, ..., xn}, does there exist a logical assignment?
The satisfiability and 3-satisfability problems are the fundamental problems of combinatorial search; they contain the main components of a complex computational problem and in a very simplified form. It is required to make n independent decisions (assignment to all xi) so as to fulfill a set of constraints. There are different ways to execute each constraint individually, but the solutions will have to be combined so that all constraints are executed simultaneously.
Now let us link the computational complexity embodied in the SAT and 3-SAT problems with another (at first glance) complexity represented by the search for independent sets and vertex coverings in graphs, namely: we show that 3-SAT ≤P An independent set. The main difficulty in such proofs is obvious: in the 3-SAT problem, we are talking about assigning values to Boolean variables subject to constraints, whereas the problem of an independent set is aimed at choosing vertices in the graph. To solve an instance of the 3-SAT problem using the black box for the independent set problem, it is necessary to somehow encode all these Boolean constraints at the nodes and edges of the graph so that the feasibility criterion matches the existence of a large independent set.
This technique demonstrates the general principle of designing complex information Y ≤PX: building “regulators” of the components in task X to represent what is happening in task Y.
(8.8) 3-SAT ≤P Independent set.
Proof . There is a black box for the independent set problem; we want to solve an instance of the 3-SAT problem, consisting of the variables X = {x1, ..., xn} and the conditions C1, ..., Ck.
To properly look at the problem of information, it should be understood that there are two conceptually different points of view on a 3-SAT instance.
- The first way to represent the 3-SAT instance was proposed earlier: for each of the n variables, an independent decision of 0/1 is made, and success is achieved when one of the three ways to fulfill each condition is reached.
- The same 3-SAT instance can be presented differently: you need to select one literal from each condition, and then find a logical assignment, as a result of which all these literals give the result 1 with all the conditions. So, success is achieved if you can choose a literal from each condition so that no two selected literals “conflict”; we say that the conflict of two literals arises when one equals the variable xi and the other denies it. If we manage to avoid conflicts, we can find a logical assignment, as a result of which the selected literals from each condition give the result 1.
The following is based on the second representation of the 3-SAT instance; we encode it using independent sets in the graph. First, we construct the graph G = (V, E), consisting of 3k nodes, grouped into k triangles, as shown in Fig. 8.3. Thus, for i = 1,2, ..., k, three vertices vi1, vi2, vi3 are constructed, connected with each other by edges. Each vertex is assigned a label; vij is marked with the j-th literal from the Ci condition of the 3-SAT instance.
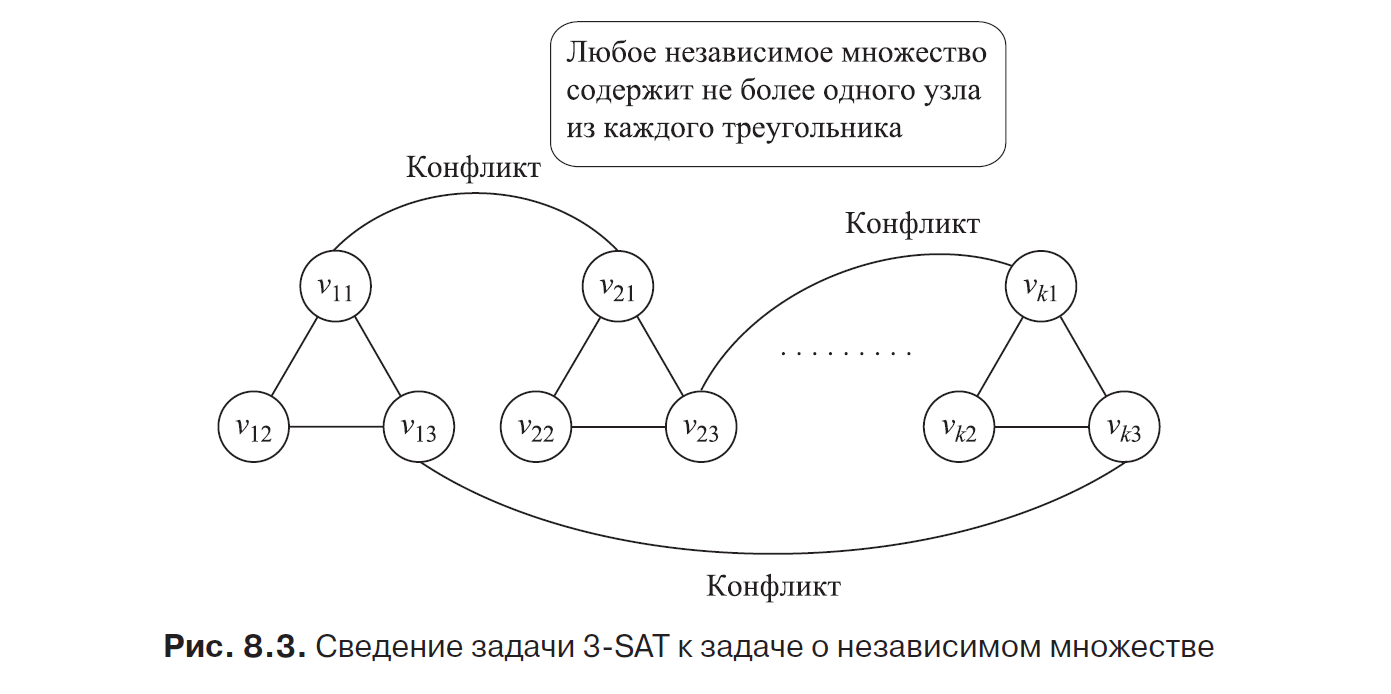
Before proceeding, consider what independent sets with size k look like on this graph: since two vertices cannot be chosen from one triangle, they consist of all the ways to select one vertex from each triangle. This is how our goal of choosing a literal in each condition is fulfilled, which gives the result 1; but so far we have done nothing to prevent a conflict between the two literals.
Conflicts will be encoded by adding new edges to the graph: we connect each pair of vertices whose labels correspond to conflicting literals with an edge. Will this lead to the destruction of all independent sets of size k or does such a set exist? It depends on whether you can select one node from each triangle so that no conflicting pairs of nodes are chosen. But after all, exactly what is required in the 3-SAT instance!
It is stated that the original instance of the 3-SAT problem is fulfilled if and only if the constructed graph G has an independent set with a size of at least k. First, if the 3-SAT instance is executable, then each triangle in the graph contains at least one node whose label gives the result 1. Let S be a set consisting of one such node in each triangle. The set S is independent; if between two nodes u, v should conflict; but this is impossible, since both give the result 1.
Conversely, suppose that the graph G contains an independent set S with a size of at least k. Then, first of all, the size of S is exactly k, and it must contain one knot from each triangle. Further, it is stated that there is a logical assignment of ν for variables in the 3-SAT instance, which has the property that the labels of all nodes S give the result 1. How to build such an assignment of ν? For each variable xi, if neither xi nor is used as a node label in S, we assign ν (xi) = 1. Otherwise, either xi or is a node label in S; because if one node in S were labeled xi and the other, then these two nodes would be connected by an edge, which would contradict our assumption that S is an independent set. If xi is a label of a knot in S, we assign ν (xi) = 1; otherwise, the assignment ν (xi) = 0 is performed. With this construction of ν, all the labels of the nodes in S give the result 1.
Since G contains an independent set with a size of at least k, if and only if the original 3-SAT instance was executable, the rollup is complete.
Link to the review of the book itself here
And now we give a formal definition of assigning values satisfying a set of conditions. The logical assignment for X is the assignment of a value of 0 or 1 to each xi; in other words, it is a function ν: X → {0,1}. The assignment of v implicitly sets the truth value, the opposite of xi. An assignment satisfies condition C if after it C gives a result of 1 according to the conditions of Boolean logic; this is equivalent to the requirement that at least one of the literals in C has the value 1. The assignment fulfills the set of conditions C1, ..., Ck if, as a result, its all Ci give the result 1; in other words, if as a result of its conjunction
The logical assignment of ν, which sets the value of 1 to all three variables, is not fulfilling, because the second of the listed conditions is not fulfilled with it; on the other hand, the assignment of ν ', which sets all variables to 0, is fulfilling.
Now we can give the formulation of the problem of feasibility, also denoted by SAT:
For a given set of conditions C1, ..., Ck with respect to the set of variables X = {x1, ..., xn}, does a performing logical assignment exist?
There is a special case of SAT, which has equivalent complexity, but is more understandable; in it all conditions contain exactly three literals (corresponding to different variables). Let's call this task a 3-satisfiability problem, or 3-SAT:
')
For a given set of conditions C1, ..., Ck, each of which has a length of 3, in the set of variables X = {x1, ..., xn}, does there exist a logical assignment?
The satisfiability and 3-satisfability problems are the fundamental problems of combinatorial search; they contain the main components of a complex computational problem and in a very simplified form. It is required to make n independent decisions (assignment to all xi) so as to fulfill a set of constraints. There are different ways to execute each constraint individually, but the solutions will have to be combined so that all constraints are executed simultaneously.
Reduction of the 3-SAT problem to the independent set problem
Now let us link the computational complexity embodied in the SAT and 3-SAT problems with another (at first glance) complexity represented by the search for independent sets and vertex coverings in graphs, namely: we show that 3-SAT ≤P An independent set. The main difficulty in such proofs is obvious: in the 3-SAT problem, we are talking about assigning values to Boolean variables subject to constraints, whereas the problem of an independent set is aimed at choosing vertices in the graph. To solve an instance of the 3-SAT problem using the black box for the independent set problem, it is necessary to somehow encode all these Boolean constraints at the nodes and edges of the graph so that the feasibility criterion matches the existence of a large independent set.
This technique demonstrates the general principle of designing complex information Y ≤PX: building “regulators” of the components in task X to represent what is happening in task Y.
(8.8) 3-SAT ≤P Independent set.
Proof . There is a black box for the independent set problem; we want to solve an instance of the 3-SAT problem, consisting of the variables X = {x1, ..., xn} and the conditions C1, ..., Ck.
To properly look at the problem of information, it should be understood that there are two conceptually different points of view on a 3-SAT instance.
- The first way to represent the 3-SAT instance was proposed earlier: for each of the n variables, an independent decision of 0/1 is made, and success is achieved when one of the three ways to fulfill each condition is reached.
- The same 3-SAT instance can be presented differently: you need to select one literal from each condition, and then find a logical assignment, as a result of which all these literals give the result 1 with all the conditions. So, success is achieved if you can choose a literal from each condition so that no two selected literals “conflict”; we say that the conflict of two literals arises when one equals the variable xi and the other denies it. If we manage to avoid conflicts, we can find a logical assignment, as a result of which the selected literals from each condition give the result 1.
The following is based on the second representation of the 3-SAT instance; we encode it using independent sets in the graph. First, we construct the graph G = (V, E), consisting of 3k nodes, grouped into k triangles, as shown in Fig. 8.3. Thus, for i = 1,2, ..., k, three vertices vi1, vi2, vi3 are constructed, connected with each other by edges. Each vertex is assigned a label; vij is marked with the j-th literal from the Ci condition of the 3-SAT instance.
Before proceeding, consider what independent sets with size k look like on this graph: since two vertices cannot be chosen from one triangle, they consist of all the ways to select one vertex from each triangle. This is how our goal of choosing a literal in each condition is fulfilled, which gives the result 1; but so far we have done nothing to prevent a conflict between the two literals.
Conflicts will be encoded by adding new edges to the graph: we connect each pair of vertices whose labels correspond to conflicting literals with an edge. Will this lead to the destruction of all independent sets of size k or does such a set exist? It depends on whether you can select one node from each triangle so that no conflicting pairs of nodes are chosen. But after all, exactly what is required in the 3-SAT instance!
It is stated that the original instance of the 3-SAT problem is fulfilled if and only if the constructed graph G has an independent set with a size of at least k. First, if the 3-SAT instance is executable, then each triangle in the graph contains at least one node whose label gives the result 1. Let S be a set consisting of one such node in each triangle. The set S is independent; if between two nodes u, v should conflict; but this is impossible, since both give the result 1.
Conversely, suppose that the graph G contains an independent set S with a size of at least k. Then, first of all, the size of S is exactly k, and it must contain one knot from each triangle. Further, it is stated that there is a logical assignment of ν for variables in the 3-SAT instance, which has the property that the labels of all nodes S give the result 1. How to build such an assignment of ν? For each variable xi, if neither xi nor is used as a node label in S, we assign ν (xi) = 1. Otherwise, either xi or is a node label in S; because if one node in S were labeled xi and the other, then these two nodes would be connected by an edge, which would contradict our assumption that S is an independent set. If xi is a label of a knot in S, we assign ν (xi) = 1; otherwise, the assignment ν (xi) = 0 is performed. With this construction of ν, all the labels of the nodes in S give the result 1.
Since G contains an independent set with a size of at least k, if and only if the original 3-SAT instance was executable, the rollup is complete.
Link to the review of the book itself here
Source: https://habr.com/ru/post/321778/
All Articles