As I made the fastest resize of images. Part 0

Hello, my name is Sasha, I wrote the fastest image resize for modern x86 processors. I say this because all the other libraries that I managed to find and test turned out to be slower. I started this task when I worked on optimizing image resize on the fly in Uploadcare . We decided to open the code and as a result, the Pillow-SIMD project appeared. Anyone can easily use it in a Python application.

Any code is executed on a specific hardware and good optimization can be achieved only by understanding its architecture. In total, I plan to release 4 or 5 articles in which I will tell you how to use the knowledge of iron architecture to optimize a real task. By example, I want to encourage you to optimize other applied tasks. The first two articles will be published within a week, the rest - as soon as they are ready.

About the task

By “resize images” I understand image resizing by resampling using the convolution method. Ramping is performed on an array of 8-bit RGB pixels into memory, without taking into account decoding and encoding of images, however, taking into account the allocation of memory for the final image and taking into account the preparation of coefficients required for a particular operation.

That's so strict. No tricks (like decoding from a smaller image dzhipega) and no combination of algorithms, only an honest measurement of the work of a specific algorithm. Tricks and optimizations of particular cases can be applied later; they are not the subject of this series of articles.

... using the resampling method of convolutions. What?

To make it clear what specifically needed optimization, I will tell you what resampling is convolution. Convolution (correctly speaking, convolution of discrete values , since image pixels are discrete) is a very simple mathematical operation. We have some number 1 values ​​(coefficients) and a number 2 values ​​(data, in our case, the intensity of the pixel channels). The result of the convolution of these two series will be the sum of the products of all members in pairs. So simple - the sum of the works. Matan ended before it started.

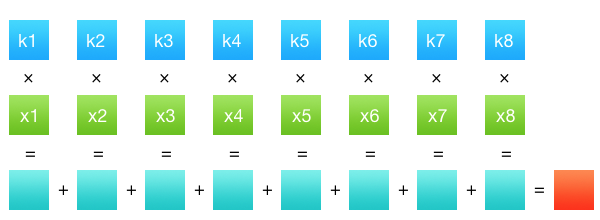
It remains to understand exactly how this operation is related to the resize. Number 2 is the number of pixels in the original image. A number of values ​​ „–1 are the coefficients obtained from the filter. A filter is a function that determines how exactly we will collapse the values. Maybe you noticed in the resize window in Photoshop or another graphic editor a drop-down menu with filters - bilinear, bicubic, sometimes Lanczos. This is this filter. But the resulting convolution value is the intensity of one channel of one pixel of the final image. Those. to get an image of size M × N pixels, we need to do M × N × C convolution operations, where C is the number of color channels. Yes, counting the entire pixel in a single operation will not work, the values ​​of different channels are independent and must be considered separately.

The functions of the filters are not infinite, their values ​​are not equal to zero only in the central part: for a bilinear filter, this is the range of values ​​from –1 to 1; for bicubic from –2 to 2, for Lanczos from –3 to 3 (although there are other varieties of Lanczos).

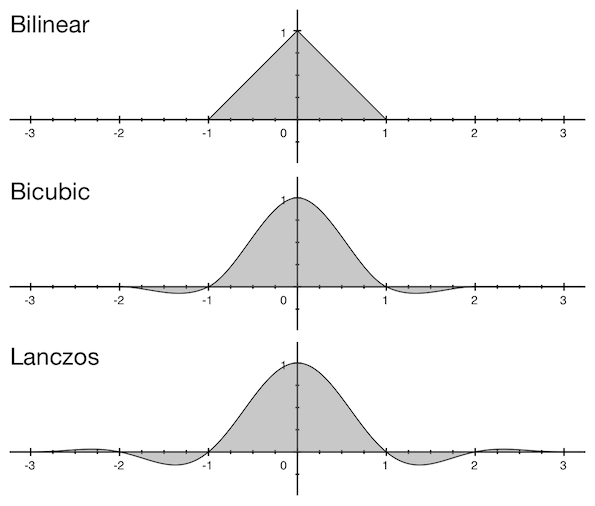
These numbers are called the filter window, since the filter is applied only in this range, and outside it is zero. Accordingly, the number of source pixels required for convolution is taken in a radius the size of the filter window multiplied by the reduction factor (or by one if an increase occurs). I think this is better explained by example. We need to reduce the image to a width of 2560 pixels to a width of 2048, using a bicubic filter. Suppose we want to find the value of the 33rd pixel of the final image. In a bicubic filter, the window size is two, and the reduction factor is 2560/2048 = 1.25, so we will need to take a row of pixels from the original image from floor((33 - 2) × 1,25) to ceil((33 + 2) × 1,25) . Those. from 38th to 44th pixel. For the same pixels, the values ​​of the coefficients are calculated.

Up to this point, I was talking about a number of coefficients and a number of pixels, overlooking the fact that the image is actually a two-dimensional structure. And it seems, by logic, that it is not the line that needs to be folded, but some area of ​​the original image. But one of the properties of bundles is that the operation can be carried out separately vertically and horizontally by making two passes. Roughly speaking, this makes it possible to reduce the complexity of a single convolution from O (n²) to O (2n) (actually less, but still significant).

Why are convolutions nevertheless

In general, the phrase “image resize” carries a minimum of information about what needs to be done. She says that we should get an image of a finite size using the original, while preserving the geometry of the objects depicted. But you can use the original image in different ways. You can, for example, for each end pixel, put in correspondence one pixel from the source and take it without changes. This is called the nearest neighbor method. The picture is rough, torn, unpleasant:

This is because a very small part of the original pixels was used in the final image (in the example above, less than one percent). Information from those pixels that did not fall into the final image, we lost.

And here is what resampling looks like using convolutions:

Re-sampling using convolutions correctly considers the contribution of each source pixel to the final image. It is universal, because gives an equally good and predictable result for a wide range of scaling factors, does not contain geometry distortions at the local level (with the proviso that a filter is used that does not give such distortions, as some filters do). And in general, he is all so correct and good from all sides, except for one thing: performance.

Pillow

Pillow is a Python image library developed by a community led by Alex Clark and Eric Soroos. Uploadcare Pillow was used before I joined the team. Then it seemed strange to me - work with images was one of the main tasks, why was it necessary to take for her a library tied to the language. Isn't it better to take the same ImageMagick, which has a ton of functions used by a million developers, it should be sure that everything should be fine with performance. After several years, I can say that it was good luck both for me and for Pillow. As it turned out, the performance of both libraries at the start was about the same, but I very much doubt that I would have had the strength to do something for ImageMagick that I did for Pillow.

Pillow is a fork of a very old PIL library. Historically, no convolutions were used for resizing in the PIL. The first implementation of resize on convolutions in the PIL appeared in version 1.1.3 and was available when using the ANTIALIAS filter, the name of which emphasized that the other filters used lower-quality algorithms. In the network, it is still possible to often find no longer relevant recommendations to use only the ANTIALIAS filter when resizing in the PIL (and Pillow as a receiver).

Unfortunately, ANTIALIAS had rather poor performance. I climbed into the source code to see what could be done, and it turned out that the implementation of resizing for ANTIALIAS (that is, convolution) can be used with the rest of the filters. And the constant ANTIALIAS corresponds to the Lanczos filter, which has a large window (± 3), and therefore it is rather slow. The very first optimization I wanted to do was enable convolutions for bilinear and bicubic filters. So it would be possible to use a cheaper bicubic filter (with a window of ± 2) in my application and not lose too much in quality.

Then I was interested to look at the code of the resize itself. I easily found it in this module . And even though I write mostly on python, I immediately noticed several questionable places in terms of performance. After several optimization, I received a 2.5-fold increase (this will be described in the next article ). Then I began to experiment with SIMD, translate all calculations into whole numbers, aggressively develop loops and group calculations. The task was extremely interesting, in my head there were always a couple more ideas on how to improve performance. I plunged deeper and deeper into the rabbit hole, periodically testing another hypothesis.

Gradually, the code got bigger and faster. Part of the work was given back to Pillow. But the SIMD code was difficult to transfer because it was written for a specific architecture, and Pillow was a cross-platform library. Therefore, it was decided to make a non-cross-fork fork Pillow-SIMD . The Pillow-SIMD versions are fully compatible with the original Pillow versions and add acceleration to some operations.

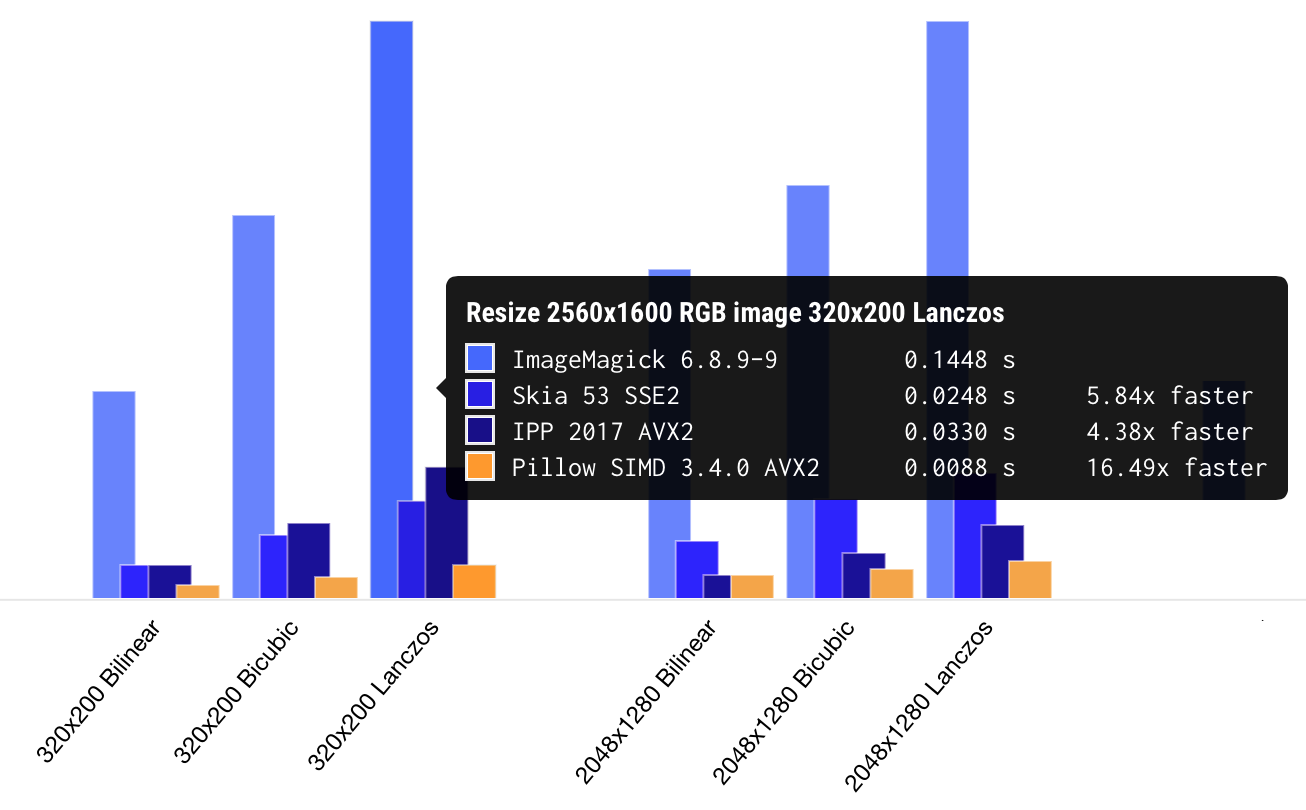
In the latest versions of the Pillow-SIMD, the AVX2 resizes 15 to 30 times faster than the original PIL. As I said at the very beginning, this is the fastest implementation of a high-quality resize that I was able to test. You can see the page on which the results of benchmarks of different libraries are collected.

What pleases me in the case of Pillow and Pillow-SIMD is that these are real libraries that can be used even by a novice developer. This is not a piece of code published on Stack Overflow, which is not clear where to stick. And not “primitive blocks”, from which, as from the constructor, each operation must be assembled. And not even a complicated C ++ library with a confusing interface that compiles for half an hour. This is one line of installation, one line of import of the library, one line of image loading and, “hey, mom, look, I use the fastest resize in my application”.

Performance measurements

In the articles I will post the performance measurements in the form of a table in which the original image with a resolution of 2560 × 1600 pixels is resized to 320x200, 2048x1280 and 5478x3424 resolutions using the bilinear, bicubic and Lanczosh filter (that is, 9 operations in total). The original image is taken large enough not to fit completely into the cache of the processor of the third level. In this case, the actual content of the image does not matter in terms of performance, you can resize at least an empty white sheet, even black, though your cat's photo. Here is an example of the results of the Pillow library version 2.6, before any optimizations.

 Scale 2560×1600 RGB image to 320x200 bil 0.08927 s 45.88 Mpx/s to 320x200 bic 0.13073 s 31.33 Mpx/s to 320x200 lzs 0.16436 s 24.92 Mpx/s to 2048x1280 bil 0.40833 s 10.03 Mpx/s to 2048x1280 bic 0.45507 s 9.00 Mpx/s to 2048x1280 lzs 0.52855 s 7.75 Mpx/s to 5478x3424 bil 1.49024 s 2.75 Mpx/s to 5478x3424 bic 1.84503 s 2.22 Mpx/s to 5478x3424 lzs 2.04901 s 2.00 Mpx/s 

The second column here is the time in seconds, and the third is the bandwidth of the original image for this operation. That is, if the operation took 0.2 seconds, then the bandwidth would be 2560 × 1600 / 0.2 = 20.48 megapixels per second.

The original image is resized to 320 × 200 resolution in 164 milliseconds. Well, sort of nice. Maybe you do not need to optimize, leave as is? Well, if you remember that the resolution of photos from mobile phones now has an average size of 12 megapixels, then everything turns out not so rosy. The photo from the iPhone will decrease half a second without taking into account the unpacking. Considering other operations, per minute you can process ≈80 pictures, and per hour - about 5000. The current load on our service is about 130 thousand requests per hour. We would need 26 AWS c4.large servers running at the limit to cope with such a load. In reality, we have only 4 servers involved, the load on which during the hot hours is about 40%.

If such an effect could extrapolate to the scale of the planet and replace all the code that deals with the resize of pictures with a more efficient one, the benefits would be enormous. Tens of thousands of servers saved, hundreds of kilowatts of electricity. And this is one millionth of world consumption. Yes, it would be possible to save the planet!

Next: Part 1, general optimizations