Analysis of the effectiveness of the factorization method on elliptic curves. Practice
The problem of factorization is directly related to the definition of RSA cryptographic strength, which is based on the assumption that there are no fast factorization algorithms that could crack the code in a short time, and if after some time this happens, the data will lose its relevance. In this article we will test and draw conclusions on one of the methods of factorization.
We give the definition of factorization.
Factorization of an integer is its decomposition into a product of simple factors. Such a decomposition, according to the main theorem of arithmetic, always exists and is unique (with the accuracy of the order of the factors).
We will denote the number that you want to decompose by the letter N, and the two factors, the multiplication of which will result in N, as a and b.
')
The Lenstra's factorization algorithm (factorization on elliptic curves) is one of the fastest factorization methods. It has much in common with the Pollard method (p - 1), but it works much faster, it should be noted that it is a subexponential method. The main feature of the algorithm is that the time spent on factorization depends not on the dimensionality of N, but on the size of the smallest divisor of the number N.
In detail about this method, you can read from the material in the list of references, but still give the main stages of the algorithm.
In field arithmetic, there is no division operation, which is necessary in formulas for finding the coordinates of points, so we transform the expression in the form of multiplication, and look for the inverse element using the Euclidean extended algorithm. In addition, each new calculation we produce modulo the number N.
The algorithm will complete its work when N.O.D. (N, P) is found, which is greater than 1 and less than N. In order to avoid an error in the answer, the function of finding N.O.D. should check only positive values.
Consider the time line that we need to factor in different numbers. (The result is from the program I wrote)
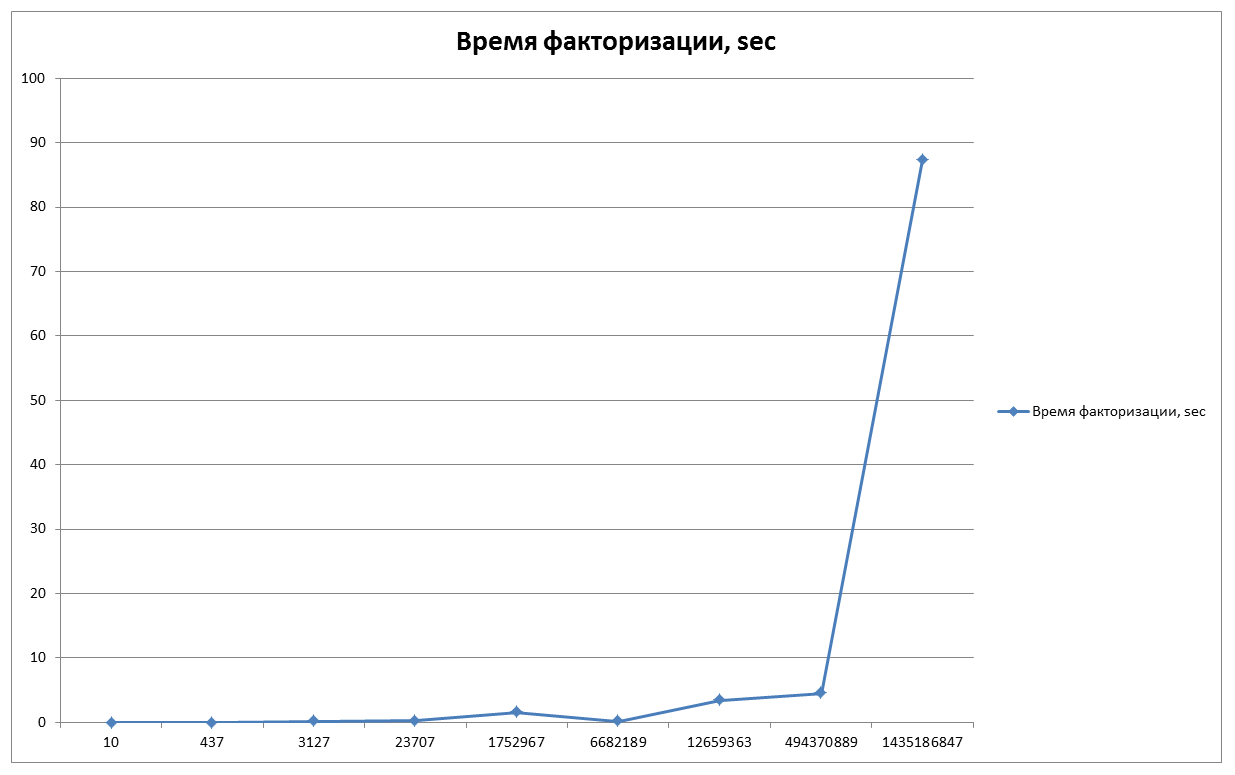
Since the curve is generated from random values, the factorization time for each new program start will be different. It depends on whether the successful curve gets to us. According to this, we will try to take the same numbers and perform factorization several more times and check the results.
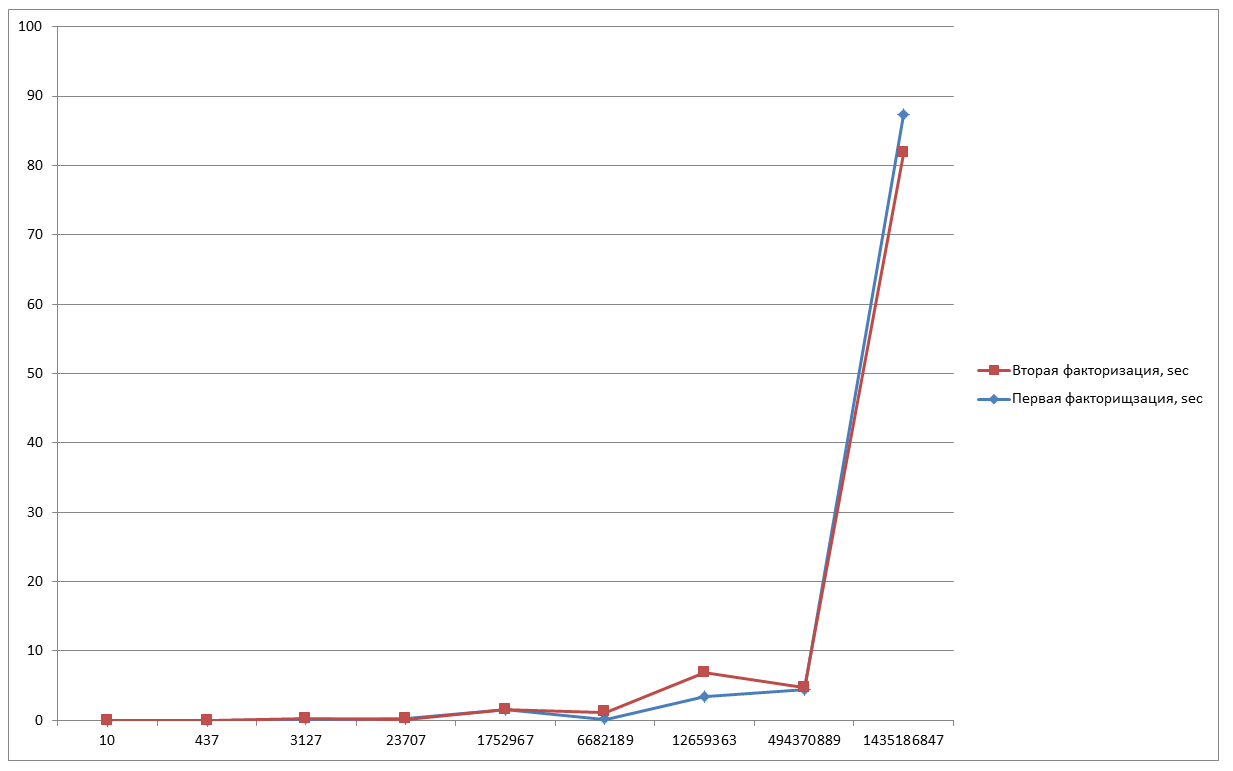
And for fixing we will make the last measurement.
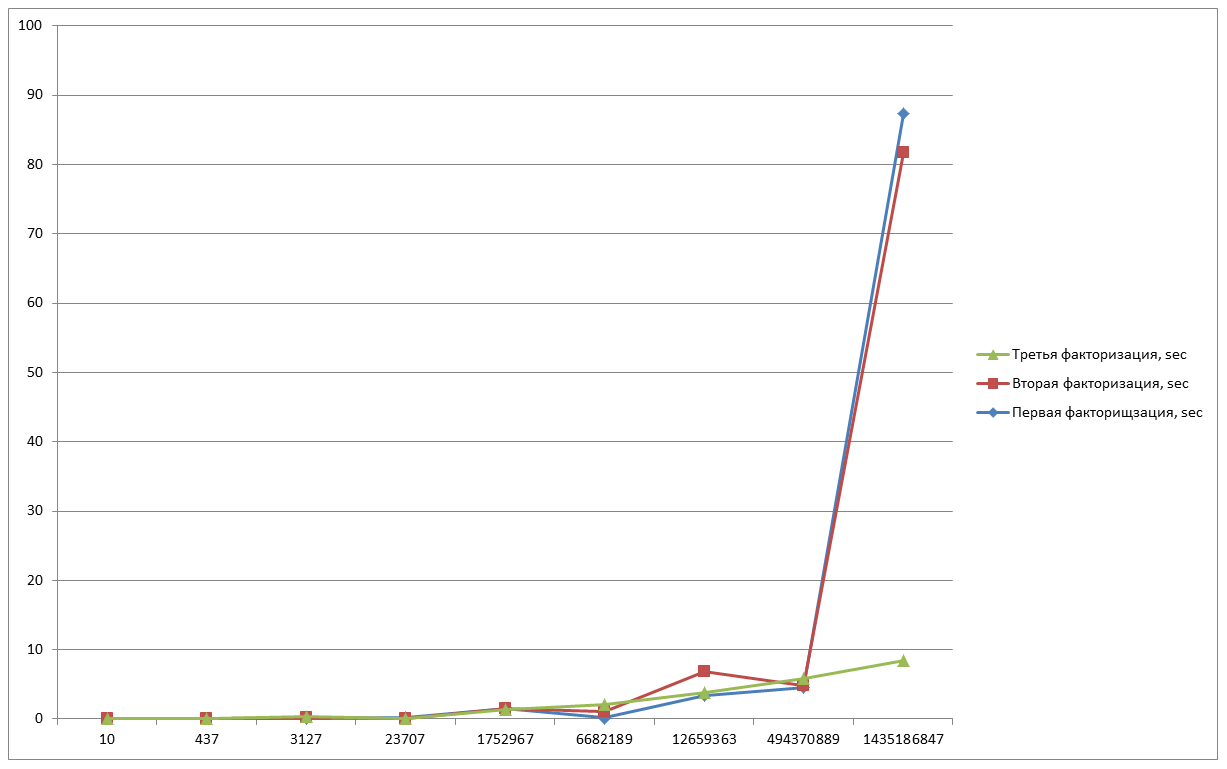
As we see in the last graph, the time spent on the last number has noticeably decreased, it is characterized by the fact that the curve is generated randomly. It should be noted that the time spent on the execution of the algorithm depends on the value of B, which we enter. I tried to take values close to the values of the two factors (a and b), but if you perform an operation on a number where the initial factors are not known even approximately, then you should choose the limit above. But the higher the limit, the more time will be spent on the calculation of points, because there will be more of them, this should be taken into account.
Should take into account the performance of the computer. I made calculations on an AMD Athlon (tm) II X4 645 processor with a frequency of 3.10 GHz. The load on the processor was about 40% when the program was running. The load on the memory was not noticed.
The algorithm works in a fairly good time, but only for relatively small values. After all, as we can see on schedule 1 and 2, the number after 1 billion in most cases has a large gap with time spent on the number 494370889, but this was expected, because, as noted earlier, the method is subexponential.
Thank you for reading my first article.
References: “Mathematical foundations of information security”
We give the definition of factorization.
Factorization of an integer is its decomposition into a product of simple factors. Such a decomposition, according to the main theorem of arithmetic, always exists and is unique (with the accuracy of the order of the factors).
We will denote the number that you want to decompose by the letter N, and the two factors, the multiplication of which will result in N, as a and b.
')
The Lenstra's factorization algorithm (factorization on elliptic curves) is one of the fastest factorization methods. It has much in common with the Pollard method (p - 1), but it works much faster, it should be noted that it is a subexponential method. The main feature of the algorithm is that the time spent on factorization depends not on the dimensionality of N, but on the size of the smallest divisor of the number N.
In detail about this method, you can read from the material in the list of references, but still give the main stages of the algorithm.
- We introduce the number N.
- Choose some value B, which is the maximum limit of the divisor number N.
- Randomly generate x, y, a values that belong to the set of integers from 0 to N-1. These values define the curve, and also x and y define the starting point P.
- We calculate b = y ^ 2-x ^ 3-ax mod n and g = N.O.D. (N, 4a ^ 3 + 27b ^ 2). It is important that g is not equal to N, otherwise we return to step 2. If 1 <g <n, then stop the calculation - a divisor is found. This option is possible with small values of the number N (for example, 10), with increasing N, this possibility occurs less and less.
- Next, you need to perform a cycle, as a result of which for each prime number p (in the limit from 2 to B-1) we calculate the point P multiplied by p ^ r, where r is the greatest degree satisfying the condition p ^ r <B.
In field arithmetic, there is no division operation, which is necessary in formulas for finding the coordinates of points, so we transform the expression in the form of multiplication, and look for the inverse element using the Euclidean extended algorithm. In addition, each new calculation we produce modulo the number N.
The algorithm will complete its work when N.O.D. (N, P) is found, which is greater than 1 and less than N. In order to avoid an error in the answer, the function of finding N.O.D. should check only positive values.
Consider the time line that we need to factor in different numbers. (The result is from the program I wrote)

N = 10 - 0.005 sec;
N = 437 - 0.019 sec;
N = 3127 - 0.055 sec;
N = 23707 - 0.191 sec;
N = 1752967 - 1.534 sec;
N = 6682189 - 0.143 sec;
N = 12659363 - 3,376 sec;
N = 494370889 - 4,484 sec;
N = 1435186847 - 87,377 sec;
Since the curve is generated from random values, the factorization time for each new program start will be different. It depends on whether the successful curve gets to us. According to this, we will try to take the same numbers and perform factorization several more times and check the results.

N = 10 - 0.016 sec;
N = 437 - 0.016 sec;
N = 3127 - 0.218 sec;
N = 23707 - 0.079 sec;
N = 1,752,967 - 1,484 sec;
N = 6682189 - 1,125 sec;
N = 12659363 - 6.906 sec;
N = 494370889 - 4,781 sec;
N = 1435186847 - 81,766 sec;
And for fixing we will make the last measurement.

N = 10 - 0.012 sec;
N = 437 - 0.022 sec;
N = 3127 - 0.156 sec;
N = 23707 - 0.205 sec;
N = 1752967 - 1.418 sec;
N = 6682189 - 1,056 sec;
N = 12659363 - 0.25 sec;
N = 494370889 - 5.488 sec;
N = 1435186847 - 14,117 sec;
As we see in the last graph, the time spent on the last number has noticeably decreased, it is characterized by the fact that the curve is generated randomly. It should be noted that the time spent on the execution of the algorithm depends on the value of B, which we enter. I tried to take values close to the values of the two factors (a and b), but if you perform an operation on a number where the initial factors are not known even approximately, then you should choose the limit above. But the higher the limit, the more time will be spent on the calculation of points, because there will be more of them, this should be taken into account.
Should take into account the performance of the computer. I made calculations on an AMD Athlon (tm) II X4 645 processor with a frequency of 3.10 GHz. The load on the processor was about 40% when the program was running. The load on the memory was not noticed.
Total
The algorithm works in a fairly good time, but only for relatively small values. After all, as we can see on schedule 1 and 2, the number after 1 billion in most cases has a large gap with time spent on the number 494370889, but this was expected, because, as noted earlier, the method is subexponential.
Thank you for reading my first article.
References: “Mathematical foundations of information security”
Source: https://habr.com/ru/post/321488/
All Articles