The method of recursive coordinate bisection for decomposition of computational grids

Introduction

Computational grids are widely used in solving numerical problems using finite difference methods. The quality of the construction of such a grid largely determines the success in solving, therefore sometimes the grids reach huge sizes. In this case, multiprocessor systems come to the rescue, because they allow to solve 2 problems at once:

1. Increase the speed of the program.
2. Work with grids of a size that does not fit in the RAM of one processor.

With this approach, the grid covering the computational domain is divided into a number of domains, each of which is processed by a separate processor. The main problem here is the “fairness” of the split: you need to choose such a decomposition, in which the computational load is distributed evenly between the processors, and the overhead costs caused by duplication of calculations and the need to transfer data between processors are small.
')
A typical example of a two-dimensional computational grid is shown in the first picture. It describes the space around the wing and the flap of the aircraft, the grid nodes are condensing to fine details. Despite the visual difference in the sizes of the multi-colored zones, each of them contains approximately the same number of nodes, i.e. You can talk about good decomposition. This is the task we will solve.

Note: since parallel sorting is actively used in the algorithm, to understand the article it is strongly recommended to know what a " Exchange exchange network with Batcher merge " is.

Formulation of the problem

For simplicity, we assume that we have single-core processors. Once again, to avoid confusion:
1 processor = 1 core . Computing system with distributed memory, so we will use the technology MPI. In practice, in such systems, multi-core processors, and thus for the most efficient use of computing resources, threads should also be used.

We will restrict grids to regular two-dimensional ones, i.e. such that a node with indices (i, j) is connected to adjacent nodes existing in i, j: (i-1, j), (i + 1, j), (i, j-1), (i, j +1) . As it is easy to see, the grid in the upper picture is not regular, examples of regular grids are shown below:


Thanks to this, it is possible to store the grid topology in a very compact way, which can significantly reduce both memory consumption and program operation time (after all, much less data needs to be sent over the network between processors).

The program receives 3 arguments at the entrance:

• n1, n2 - dimensions of a two-dimensional grid.
• k is the number of domains (parts) into which the grid is to be split.

The initialization of coordinates takes place inside the program and, generally speaking, it does not matter how it happens (you can see how it is done in the source code, the link to which is at the end of the article, but I will not dwell on this in detail).

We will store one mesh node in the following structure:

struct Point{ float coord[2]; // 0 - x, 1 - y int index; }; 

In addition to the coordinates of a point, there is also a node index, which has 2 assignments. First, it’s enough to restore the mesh topology. Secondly, it can be used to distinguish fictitious elements from normal ones (for example, for fictitious elements, the value of this field is set to -1). About what these fictitious elements are and why they are needed will be described in detail below.

The grid itself is stored in the array Point P [n1 * n2] , where the node with indices (i, j) is in P [i * n2 + j] . As a result of the program, the number of vertices in the domains must be equal to one vertex in the value (n1 * n2 / k) .

Algorithm of the decision

The procedure of recursive coordinate bisection consists of 3 steps:

1. Sorting an array of nodes along one of the coordinate axes (in the two-dimensional case along x or y).
2. Splitting a sorted array into 2 parts.
3. Recursive procedure start for received subarrays.

The basis of the recursion here is the case k = 1 (there is 1 domain left). Something like this happens:

And maybe so:


Where did the ambiguity come from? It is easy to see that I did not specify the criterion for choosing the axis, it was from here that various options appeared (at the first step, in the first case, the sorting goes along the x axis, and in the second, y). So how to choose an axis?

1. Randomly.
   
   Cheap and angry, but takes only 1 line of code and requires a minimum of time. For simplicity, the demonstration program uses a similar method (in fact, there the axis is simply reversed at each step, but from the conceptual point of view it is the same). If you want to write well - do not do so.
   
   
2. For geometrical reasons.
   
   The length of the cut is minimized (in the general case, the cut is a hyperplane, therefore in the multidimensional case it is more correct to speak about the area). To do this, select points with minimum and maximum coordinate values ​​and then measure the length based on some metric. Then it suffices to compare the obtained lengths and select the corresponding axis. Of course, it is easy to find a counterexample here:
   
   
   
   The vertical section is shorter, but intersects 9 edges, while the longer horizontal section intersects only 4 edges. Moreover, such grids are not a degenerate case, but are used in problems. However, this option represents a balance between the speed and quality of the partition: it does not require as many calculations as in the third variant, but the quality of the partition is usually better than in the first case.
   
   
3. Minimize the number of ribs cut.
   
   A cut edge is an edge connecting vertices from different domains. Thus, if this number is minimized, then the domains are obtained as more “autonomous” as possible, so we can speak of a high quality partitioning. So, in the picture above, this algorithm will select the horizontal axis. You have to pay for this speed, because you need to sort the array one by one along each of the axes, and then count the number of cut edges.

Still it is necessary to stipulate how to break an array. Let m = n1 * n2 (the total number of nodes and the length of the array P ), and k the number of domains (as before). Then we try to divide the number of domains in half, and then divide the array in the same ratio. In the form of formulas:

 int k1 = (k + 1) / 2; int k2 = k - k1; int m1 = m * (k1 / (double)k); int m2 = m - m1; 

In the example: split 9 elements into 3 domains ( m = 9, k = 3 ). Then, first, the array will be divided in the ratio of 6 to 3, and then the array of 6 elements will be split in half. As a result, we get 3 domains with 3 elements each. What you need.

Note: some may ask, why in the expression for m1 you need real arithmetic, because without using it you get the same result? The whole thing is overflow, for example, when the grid of 10000x10000 is divided into 100 domains with m * k1 = 10 ¹⁰ , which goes beyond the boundaries of the int range. Be careful!

Sequential algorithm

Having dealt with the theory, you can proceed to the implementation. For sorting, we will use the qsort () function from the C standard library. Our function will take 6 arguments:

 void local_decompose(Point *a, int *domains, int domain_start, int k, int array_start, int n); 

Here:

• a is the original mesh.
• domains is the output array in which the domain numbers for grid nodes are stored (has the same length as array a ).
• domain_start - starting index of available domain numbers.
• k is the number of elements available.
• array_start - the initial element in the array.
• n is the number of elements in the array.

First we write the basis of the recursion:

 void local_decompose(Point *a, int *domains, int domain_start, int k, int array_start, int n) { if(k == 1){ for(int i = 0; i < n; i++) domains[array_start + i] = domain_start; return; } 

If we have only 1 domain left, then we put all available grid nodes into it. Then we select the axis and sort the grid along it:

  axis = !axis; qsort(a + array_start, n, sizeof(Point), compare_points); 

The axis can be selected in one of the ways suggested above. In this example, as mentioned earlier, it simply changes to the opposite. Here, axis is a global variable that is used in the compare_points () element comparison function:

 int compare_points(const void *a, const void *b) { if(((Point*)a)->coord[axis] < ((Point*)b)->coord[axis]){ return -1; }else if(((Point*)a)->coord[axis] > ((Point*)b)->coord[axis]){ return 1; }else{ return 0 } } 

Now it remains for us to split the domains and grid nodes available to us using the appropriate formulas:

  int k1 = (k + 1) / 2; int k2 = k - k1; int n1 = n * (k1 / (double)k); int n2 = n - n1; 

And write a recursive call:

  local_decompose(a, domains, domain_start, k1, array_start, n1); local_decompose(a, domains, domain_start + k1, k2, array_start + n1, n2); } 

That's all. The full source code for the local_decompose () function is available on the github.

Parallel algorithm

Although the algorithm is the same, its parallel implementation is much more complicated. I associate this with two main reasons:

1) The system uses distributed memory, so each processor stores only its part of the data without seeing the entire grid. Because of this, when dividing an array, it is necessary to redistribute elements.

2) As a sorting algorithm, Betcher's parallel sorting is used, for its operation it is necessary that each processor have the same number of elements.

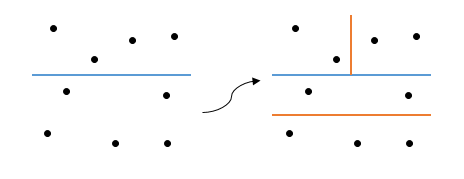
First, let's deal with the second problem. The solution is trivial - you need to enter the fictitious elements, which were mentioned in passing earlier. This is where the index field in the Point structure comes in handy. We make it equal to -1 - and we have a dummy element! It seems everything is fine, but with this decision we have significantly aggravated the first problem. In general, at the stage of dividing an array into 2 parts, it becomes impossible to determine not only the dividing element itself, but even the processor on which it is located. Let me explain this with an example: suppose we have 9 elements (a 3x3 grid) that need to be divided into 3 domains on 4 processors, i.e. n = 9, k = 3, p = 4. Then, after sorting, the dummy elements can appear anywhere (in the picture green grid nodes are marked, and red dummy elements):



In this case, the first element of the second array will be in the middle of a 2 processor. But if the dummy elements are arranged differently, then everything will change:



Here, the breaking element was already on the last processor. To avoid this ambiguity, apply a small hack: let's make the coordinates of the dummy elements as possible as possible (since they are stored in variables of type float in the program, the value will be FLT_MAX ). As a result, dummy elements will always be at the end:



The picture clearly shows that with this approach dummy elements will prevail on the latest processors. These processors will do useless work, sorting dummy items at each recursion step. However, now the definition of the splitting element becomes a trivial task, it will be located on the processor with the number:

 int pc = n1 / elem_per_proc; 

And have the following index in the local array:

 int middle = n1 % elem_per_proc; 

When a dividing element is defined, the processor containing it starts the procedure of redistributing elements: it distributes all elements to the dividing processor to the “before” processors (i.e., with numbers smaller than it), adding dummy ones if necessary. He replaces sent items with fictitious ones. In the pictures for n = 15, k = 5, p = 4:




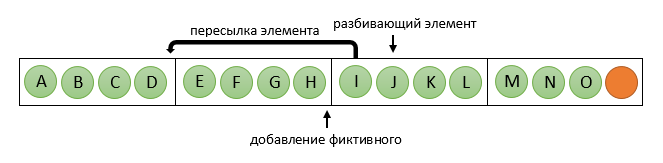
Now processors with numbers less than pc will continue to work with the first part of the original array, and the rest, in parallel, with the second part. At the same time, within the same group, the number of elements on all processors is the same (although in the second group it may be different), which allows further use of Betcher sorting. Do not forget that the case pc = 0 is possible - then it is enough to send items to the “other side”, i.e. on processors with large numbers.

The basis of the recursion in the parallel algorithm first of all should be considered the situation when we run out of processors: the case with k = 1 remains, but rather is degenerate, since in practice the number of domains is usually larger than the number of processors.

In view of the foregoing, the general scheme of the function will look like this:

Conclusion

The considered implementation of the algorithm has a number of drawbacks, but at the same time it has an undeniable advantage - it works! The source code of the program can be found on github . There is also an auxiliary utility for viewing the results. In preparing this article, we used materials from the book by M. V. Yakobovsky “Introduction to parallel methods for solving problems”.