The logic of consciousness. Part 11. Natural coding of visual and sound information

In the previous section, the requirements for a universal generalization procedure were formulated. One of the requirements stated that the result of generalization should not just contain a set of concepts, in addition, the resulting concepts must form a certain space in which the idea of ​​how these concepts correlate with each other is preserved.

If we consider concepts as “point” objects, then such a structure can be partially described by a matrix of mutual distances and presented as a weighted graph, where vertices are concepts, and each edge is assigned a number corresponding to the distance between the concepts that this edge connects.

The situation is somewhat more complicated when concepts have the nature of sets (figure below). Then formulations of the type are possible: “the concept C contains the concepts A and B”, “the concepts A and B are different”, “the concepts A and B have something in common”. If we assume that proximity is defined in the interval from 0 to 1, then we can say about the picture on the left: “proximity of A and C is 1, proximity of B and C is 1, proximity of A and B is 0).

')

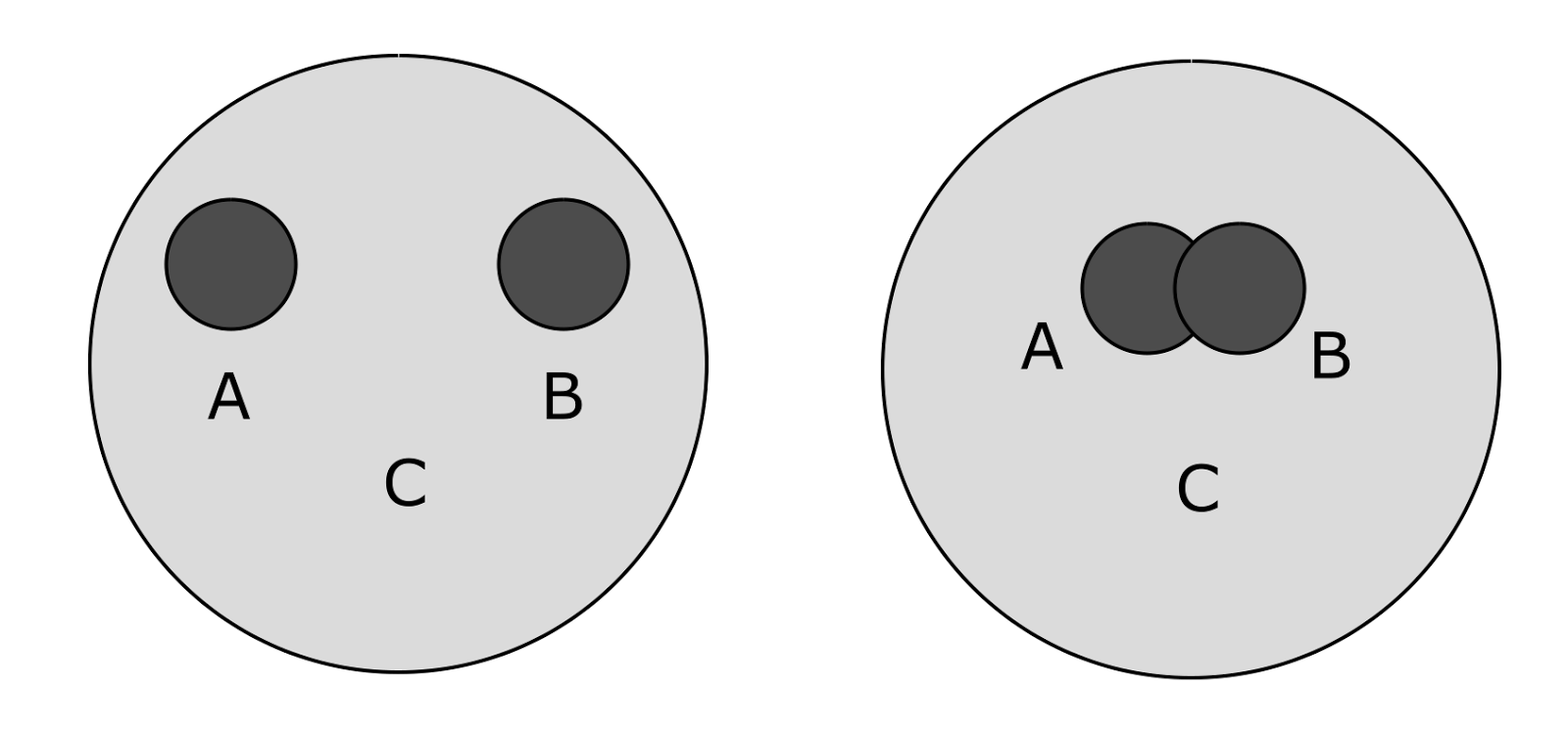
Examples of the correlation of concepts

A system with a more complex form of relationships can be written in the form of a semantic graph , that is, a directed graph, where the vertices correspond to the concepts, and the edges - the relations between them.

The question of generalization associated with the correlation of concepts is: can a system of correlation of concepts be obtained in a natural way that preserves basic properties, for example, inherent in a semantic graph, and at the same time will be convenient in generating and subsequent use? It turns out that in human biology there are examples of when such problems are solved in a rather simple and elegant way. This method is not yet a generalization, but it shows the possibility of a simple construction of a space in which the structure of proximity of concepts naturally arises.

Riddle of the optic nerve capacity

Coding of visual information can be divided into many stages. From the primary image received on the retina to the complex description of visual scenes with an understanding of what and where is depicted. In this part we will be interested in primary coding, that is, in what form the information is transmitted from the eye to the brain.


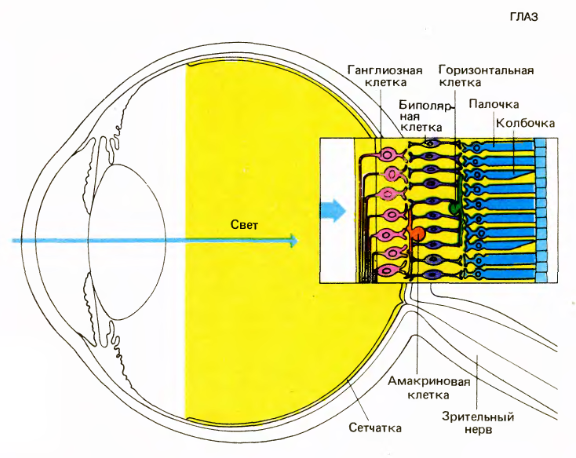
Eye and Retina (David Hubel Eye, Brain, Vision)

It all starts with the fact that the light is focused by the lens on the inner surface of the eye, forming an inverted image there. After passing through a fairly transparent layer of neurons and nerve fibers, the image reaches the cells that react to light: rods and cones. Rods are more numerous than cones. Sticks are responsible for the sensitivity in low light. Cones do not respond to weak light, they are responsible for the perception of small parts and color vision in good light.

Cones and rods are in constant impulse activity, the nature of which depends on the amount of light falling on them. This activity does not create spikes, as in neurons. It is called gradual and is manifested in a change in the cell membrane potential. The dependence itself is somewhat paradoxical - the activity weakens with increasing light intensity.


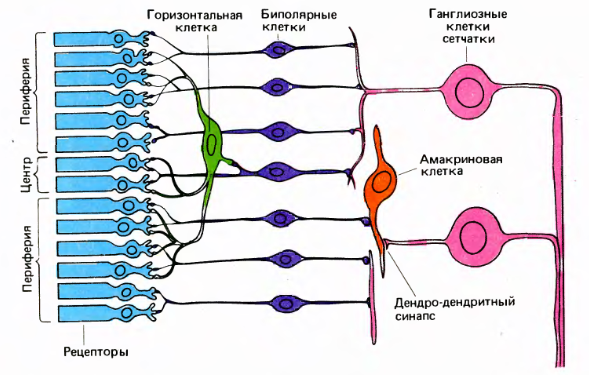
The structure of the retina (David Hubel "Eye, brain, vision")

Cones and rods send signals to horizontal and bipolar cells. Horizontal, bipolar and amacrine cells prepare signals in such a way that the ganglion cells begin to respond to a certain pattern that occurs in a small area of ​​the retina, in the center of which they are located. Ganglion cell activity is a spike. The axons of the ganglion cells form the exit of the eye, that is, the optic nerve.

Each ganglion cell has a receptive field that determines its activity. The receptive field has the shape of a circle. It distinguishes the central region and the periphery (picture above).

The most common reaction of ganglion cells is a reaction to the difference in illumination of the center and the periphery of their receptive fields. Based on this, it is customary to say that many ganglion cells react to the boundaries of the objects present in the image. At the same time, the exit of the eye is simplified as a result of the selection of contours from the original image (figure below).


Selection of borders on the image

Difficulties begin when a desire arises to understand how the optic nerve transmits visual information.

In the retina of an adult, there are 6 - 7 million cones and about 120 million rods . Potentially it would be possible to talk about the resolution of the eye in a hundred megapixels. But the optic nerve of one eye contains only about one million fibers. That is, it turns out that only one million fibers transfers all that “beautiful” picture that we see.

If we interpret the signals of the fibers of the optic nerve as information about individual points in the image, for example, contour, then it turns out that the resolution of the eye does not exceed one megapixel. And since the signals are spikes, that is, the pulses of the same amplitude, this megapixel picture is also devoid of information about any brightness levels.

A little more about the levels. In general, it is assumed that the frequency of spikes can encode analog levels. But with this there is a big difficulty. The frequency of impulses of ganglion cells is relatively small, on average about 10 - 30 Hz. But the eye is able to fully analyze the image in 13 milliseconds (Potter, MC, Wyble, B., Hagmann, CE et al. Atten Percept Psychophys (2014)). Thus, it turns out that it is unlikely that there is more than one pulse per “one frame” of an image analyzed by the eye. So about any coding brightness frequency of speech signals are not.

In addition to information about the contour, the brain also receives information about color, light transitions, and thin lines in the image. Accordingly, the question arises - how in one million fibers, without using frequency coding, can you encode all the details of visual information? Nothing remains but to assume that the coding mechanism is far from the signal of one fiber of the optic nerve describing the state of one point of the image.

Visual coding

The receptive fields of the adjacent ganglion cells overlap greatly. In this case, the central regions of receptive fields intersect only insignificantly.


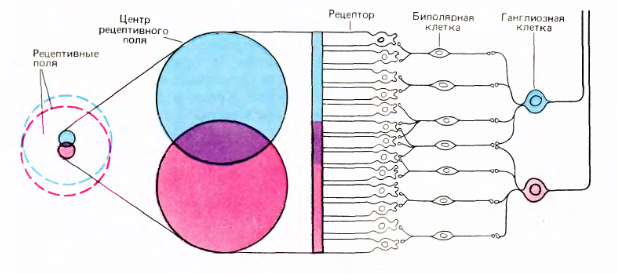
Overlap of receptive fields of retinal ganglion cells (David Hubel "Eye, brain, vision")

Ganglion cells react acutely to small light spots or dims falling on the center of their receptive field (Kuffler, SW 1953. /. Neurophysiol. 16: 37-68.). According to the type of reaction, they are divided into two types: cells with an on-center and cells with an off-center. Cells with an on-center react most strongly to a light spot that coincides with the center of the receptive field, provided that the periphery is darkened. The off-center cells react in the same way, but only their stimulus is opposite to the on-center stimulus, that is, the center must have a dark spot, and the periphery must be lit.

Both types of cells react to the opposite stimulus. They react by first suppressing their spontaneous activity for the duration of the stimulus, and then when the opposite stimulus ceases to function, the induced activity appears for some time, which gradually reaches the level of spontaneous activity.

Two types of ganglion cells are distinguished: Small cell (parvocellular.) And large cell (magnocellular, M) cells. Smaller Ρ cells are sensitive to small details and are able to distinguish colors. Large M cells are sensitive to moving objects and respond well to changes in contrast (Kaplan, E., and Shapley, RM 1989. Proc. Natl. Acad. Sci. USA 83: 2755-2757.). This division does not apply to all, for example, in cats that do not have color vision, it is customary to talk about a different classification (Enroth-Cugell, C, and Robson, JG 1966. /. Physiol. 187: 517-552.).

The response of the ganglion cells is not static. Cells do not just respond to the difference in illumination of the center and periphery. Their reaction occurs only at the moment when this difference in illumination occurs. After that, the response of the cell begins to fade quickly enough.


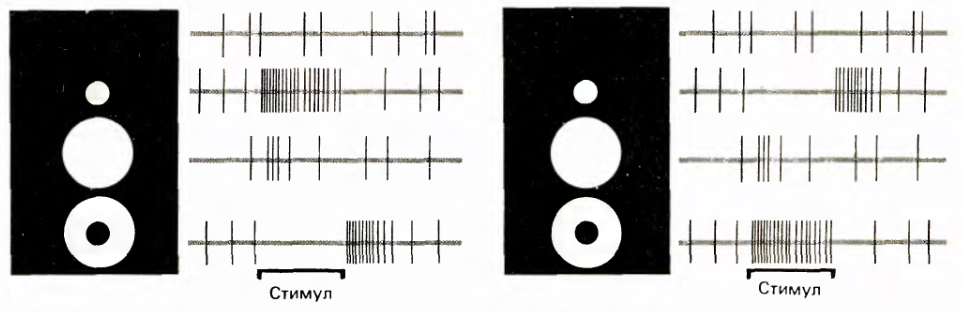
The reaction of ganglion cells to various stimuli. On the left - the reaction of the cell with the on-center, on the right - with the off-center. The sweep duration is 2.5 seconds, the vertical lines correspond to the pulses. (David Hubel Eye, Brain, Sight)

This reaction leads to the fact that in order for the image to remain visible, it must always be mobile. It was experimentally shown that if you fix the eye still relative to the image, and to do this, simply attach the light source directly to the eye, then the image quickly disappears and becomes invisible (Riggs, LA, and Ratliff, F. (1952), 'Effects of Counteracting the Normal Movements of the Eye ', J. Opt. Soc. Amer., 42, 872-873.) (Involuntary eye movements during fixation, RW Ditchburn and BL Ginsborg, J Physiolv.119 (1); 1953 Jan 28PMC1393034).

The eye is constantly in motion (figure below). Eye movements can be divided into several types. The minimum in amplitude movement is a tremor, in the image it is visible as a small comb. The amplitude of the tremor is approximately half the distance between adjacent cones. It can be assumed that in the case of a sharp border present in the image, the tremor ensures that this border crosses the sensitive area of ​​the cones, and therefore makes this border visible to them. This can be significant if the image is presented for a short time and eye drift does not have time to perform this function.


Eye movements. The size of the cells corresponds to the distance between the cones. For the central fossa, this corresponds to the size of the center of the receptive field of the ganglion cell

The rapid movements of the eyes - saccades, translate the eye from one area of ​​the image to another. Eye jumps continue between large saccades, but have a small amplitude. Such small jumps are called microsaccades; in the picture above, they are seen as straight lines. Earlier, we talked about the fact that saccades and microcades are necessary in order to train the bark of invariance to displacements and create an appropriate context space. In the intervals between microsaccades, the eyes do not remain motionless, it performs smooth arched movements, called drift. It is on the drift and the tremor is imposed, forming a characteristic comb.

The role of drift is very interesting. If you take the boundary of the object or a thin line, then the drift will ensure its displacement. Including in the direction perpendicular to this border. Due to the wave-like trajectory, drift ensures a non-zero component of the displacement in the perpendicular direction for lines and borders of any orientation. That is, when a straight line in an image drifts in an arc, on a small scale this is equivalent to the reciprocating movement of this line in a direction perpendicular to its orientation. To make it clearer, I made a short video .

At such a shift, the border or line intersects several centers of receptive fields of ganglion cells.

The figure below shows one of the possible positions of the border with respect to the receptive field of the ganglion cell. The emergence of such a position ensures the reaction of the cell with the on-center, since its center turns out to be more lighted than the periphery on average. If the border is shifted to the right so that it crosses the center of the field, the picture necessary for activating the cell with the off-center will appear, the average illumination of the periphery will be higher than the illumination of the center.


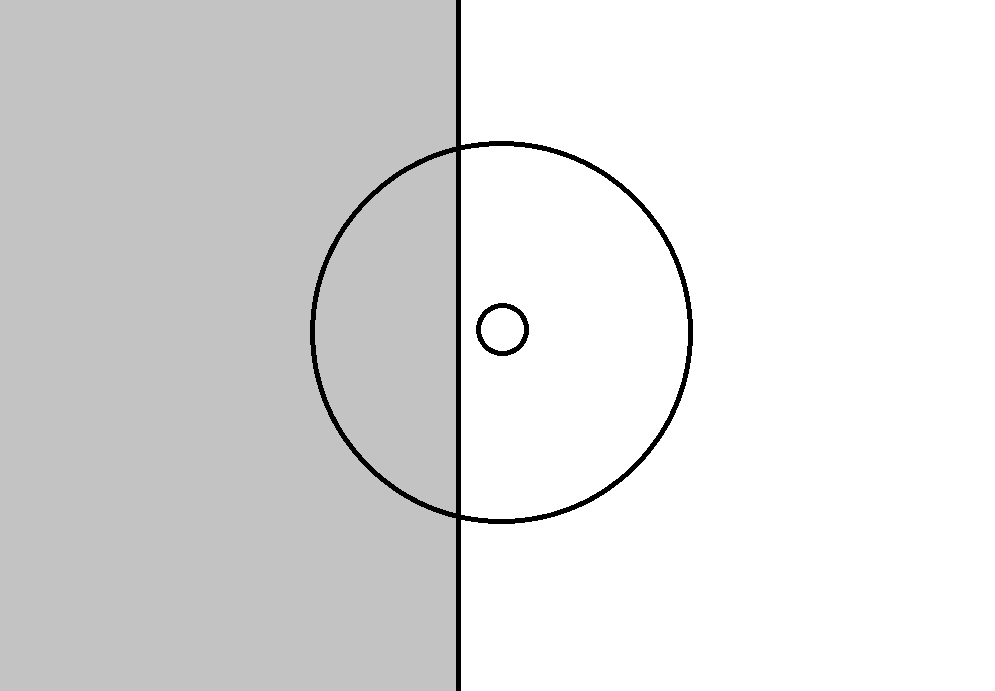
The possible position of the border in the image in relation to the receptive field of the ganglion cell and the center of this field

Accordingly, the displacement of the border during the drift creates potential conditions for the activation of those ganglionic on and off cells, the receptive fields of which it crosses during its displacement.

However, not all ganglion cells, whose receptive fields are affected by drift, can activate. Some ganglion cells have directional sensitivity (direction-selective ganglion cells - DSGC). To trigger such ganglion cells, it is necessary that the border does not just appear in the receptive field of the cell, but so that it comes from a certain side, which is preferable for this cell (Barlow HB, Hill RM (1963)). of the rabbit's retina. Science 139: 412-414).

The directional selectivity of ganglion cells turns out to be very broad (Organization and development of the direction-selective circuits in the retina, Wei Wei, Marla B. Felleremail, Trends in Neurosciences Volume 34, Issue 12, p638–645, December 2011). A direction-sensitive cell can give an answer in the range of 180 degrees, that is, for half of all possible border orientations (figure below).


An example of the range of directions causing the response in directionally sensitive ganglion cells (Wei Wei, Marla B. Felleremail, Trends in Neurosciences Volume 34, Issue 12, p638–645, December 2011).

Directional sensitivity in combination with the drift transform the corresponding ganglion cells into border orientation detectors. Drift moves along the undulating trajectory of the border. This is equivalent to the translational movement of the boundary in the direction perpendicular to this boundary. The cell for which this direction falls within its working range creates a response signal.

We will now look at a somewhat simplified model to show the main idea. We will not dwell on the reverse course, which may occur for some combinations of directions and the shape of the arc and the role of on and off cells.

A wide range of sensitivity makes a single ganglion cell a “bad” orientation detector, but things don’t get that bad if you take several of these detectors at once. For example, take an ordered set of 16 detectors, describing various possible orientations of the boundary (figure below). Let each detector react to the image of the border if its orientation falls in the range plus or minus 90 degrees from the detector's own orientation. That is, each such detector will respond to half of all possible directions.


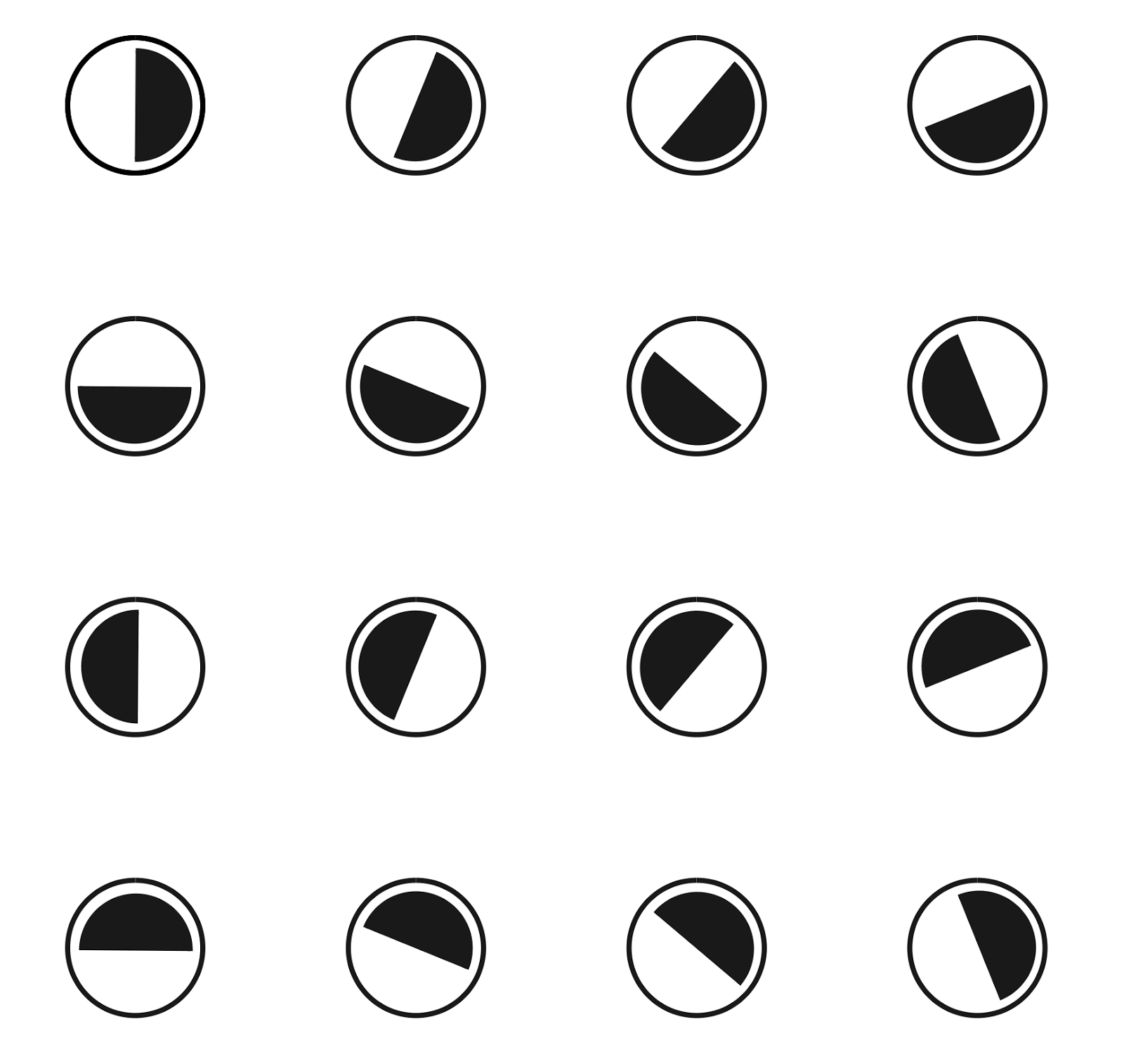
A set of 16 detectors sensitive to different orientations of the border. Showing preferred orientation. Each detector operates in the range of -90 degrees to +90 degrees to the preferred direction

If such a set of detectors provide an image of the boundary, then approximately half of them will work (we assume that the detectors are triggered, for which this image lies on the border of their sensitivity). As a result, we get a picture of the activity like the one shown in the figure below.


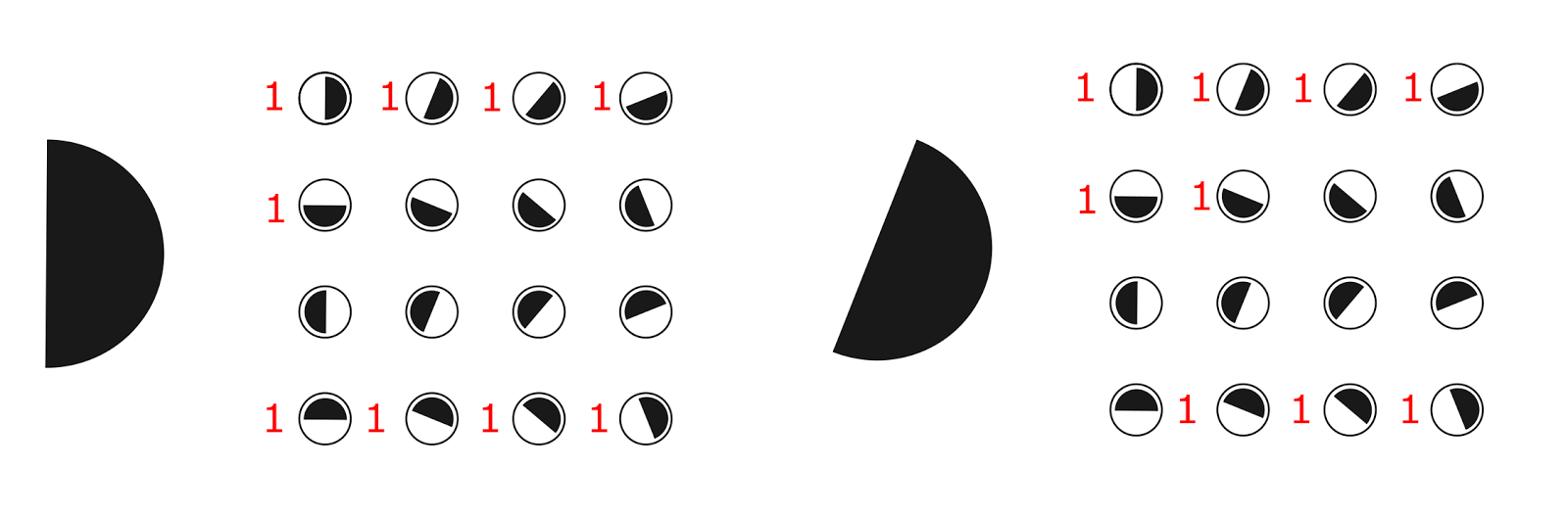
Trigger pattern of orientation detectors for different images

If we write the picture of activity as a binary vector, we get a sequence, part of which is shown in the figure below.


The sequence of binary codes corresponding to the sequence of orientations

This sequence is similar to the Gray code (F. Gray. Pulse code communication, March 17, 1953 (filed Nov. 1947). US Patent 2,632,058), with the difference that in the Gray code one bit changes in the Gray code, and in our example two. A remarkable property of the codes received is the smoothness of their transitions. Smoothness arises due to the fact that when the angle is changed, detectors are added for which the orientation of the boundary begins to fall within their range and those for which the orientation goes out of their range no longer work. This leads to the fact that with a small change in the angle, changes affect only a small number of detectors, most of which retain their state. If the angle difference exceeds the tracking range, then there are no common elements in the codes.

The scalar product of such binary vectors can be used as a measure of proximity between their respective directions. The closer the angle, the more common units, the higher the value of the scalar product.

Create an artificial retina as a rectangular grid of "coarse" detectors. We distribute the preferred directions of the detectors randomly. Let's give on a retina the image. A picture of the activity of the detectors will appear (figure below).


Image example (left), trace of activity of detectors (in the middle), decomposition into concepts (right) (vision modeling program, D. Shabanov)

The resulting picture will repeat the overall contour of the image. At the same time, in each place of the contour, the activity of the detectors will not only reproduce the shape of the contour, but will create a pattern encoding the direction of the border in this particular place.

Let's form a set of concepts necessary to describe the image. To do this, as we have done before, we divide the image into areas. For each of the areas we introduce a set of possible orientations. As a result, we get a set of concepts in which each concept will describe the orientation of the border in a particular place. In the figure above, the right fragment shows how the original image described in such terms will look.

Let's compare each concept with a binary code. This code can be obtained by collecting from the retina a pattern of detectors corresponding to the boundary that describes the concept. The full image can be written as a long binary vector, the dimension of which is equal to the total number of detectors. The code of each concept has the same dimension. In this case, only those digits that correspond to the place of the concept in the image are significant for such a code. The place on the image can be perceived as a mask, applying which you can get the concept code to the full code of the image (figure below). As a result, the code of each concept will contain a large number of zeros and a relatively small number of ones.

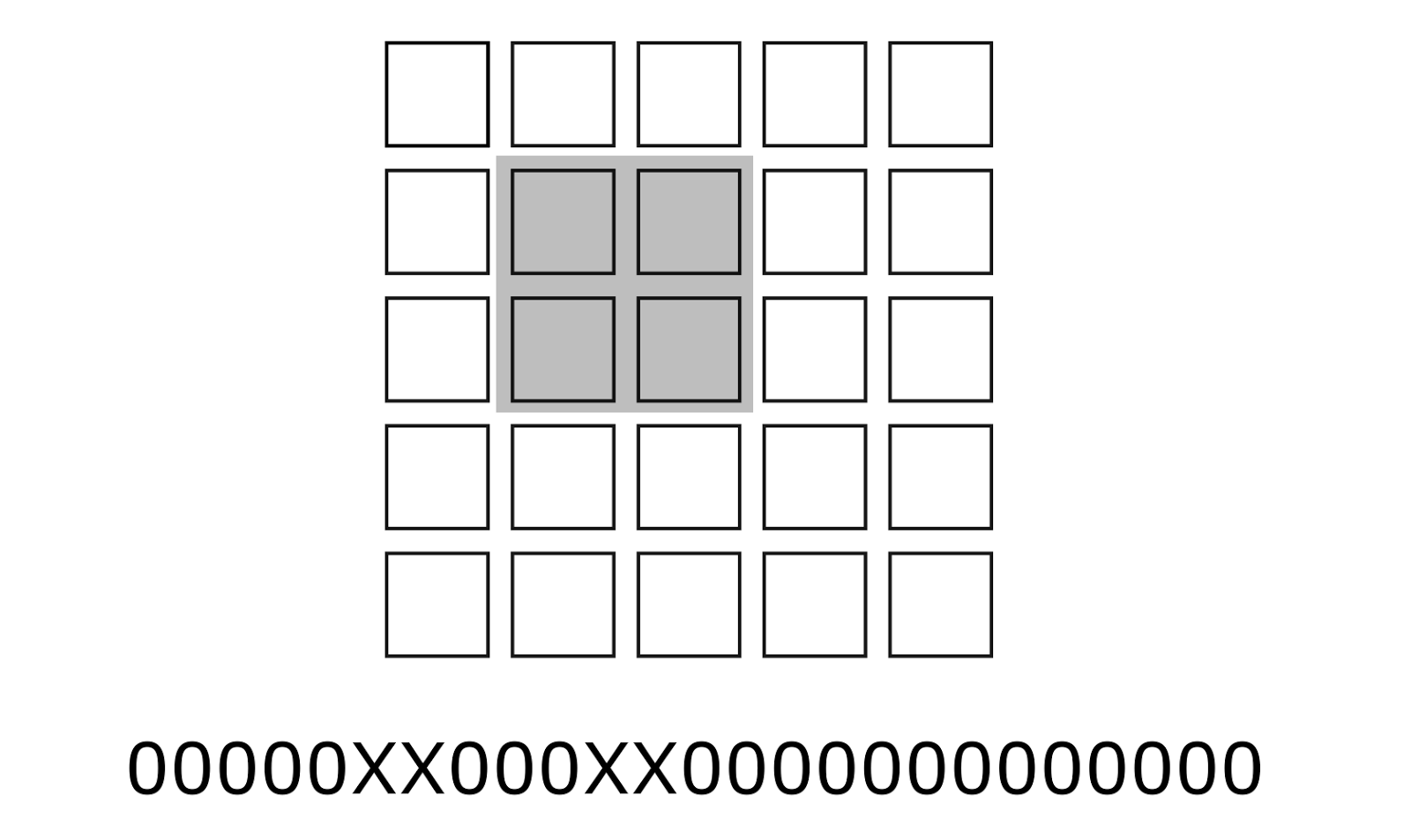
An example of the position (mask) of significant bits of a concept in a common long code. Place concepts highlighted in gray

Accordingly, with this coding, the border of the same orientation acquires a different code depending on its position in the image. Different positions correspond to different positions of the boundary of the same orientation. We can select areas (masks) that form concept codes so that they intersect each other (figure below). Then these concepts will have common detectors. This means that if there are common units in the intersection area, they will be common to both concepts. This gives a very interesting effect.

Related concepts are similar in their binary code. The scalar product of code binary vectors for such concepts will be the greater, the closer to each other these concepts. Moreover, the proximity of concepts with this approach is taken into account not in the two-dimensional space “coordinates on the image”, but in the three-dimensional space “coordinates on the image - orientation of the border”. That is, when determining the proximity of concepts, their code automatically takes into account both their proximity on the image plane, and the proximity of their orientations.


The intersection of the spatial domains of two concepts and their common description elements

In the mammalian retina, up to 20 different types of ganglion cells are distinguished, differing in their response to local contrast, direction and speed of movement, color (Wässle H, Peichl L, Boycott BB (1981)). Nature 292: 344-345 ) (DeVries SH, Baylor DA (1997) Mosaic arrangement of ganglion cell receptive fields in rabbit retina. J Neurophysiol 78: 2048-2060). All these cells create a uniform retinal coating. Accordingly, it can be said that the retina simultaneously forms two dozen descriptions that are transmitted to the brain (Rodieck RW (1998) The first steps in seeing. Sinauer, Sunderland MA). This coding includes detailed information about the shape and color of objects visible to the eye. At the same time, the signal transmitted through one axon fiber carries extremely “inaccurate” information, as it relates to a ganglion cell with a wide range of perception. The set of signals belonging to one region resolves this inaccuracy and creates a code that already quite clearly describes, for example, the angle of local contrast, the visible color or information about the movement of an object.

The signal of ganglion cells is formed due to the interaction of horizontal, bipolar and amacrine cells of the retina. Highlighting certain properties of the image, they translate this into signals of the ganglion cells. In this case, it can be assumed that the same ganglion cells can participate in several coding systems at once. In this case, binary codes related to different descriptions are superimposed on each other, which, with sufficient bit depth and sparsity of coding, does not interfere with reliably restoring the original signals. This may explain the origin of spontaneous spikes observed, for example, on and off cells in the absence of a characteristic stimulus. These spontaneous spikes can be, for example, a piece of code indicating the brightness or color of what is now in this area.

Color vision is based on the fact that a mosaic of cones different in their color sensitivity is randomly distributed on the retina. Cones are susceptible to long (L-cone), medium (M-cone) and short (S-cone) light waves (Kaiser PK, Boynton RM: Human color vision, edn 2. Washington, DC: Optical Society of America; 1996 .). An example of the distribution of color cones in the central fossa of the eye is shown in the figure below. The central fossa has the greatest sharpness of vision and consists almost entirely of cones sensitive to color, but requiring more light than sticks. For this reason, in low light, the central fossa is blind.


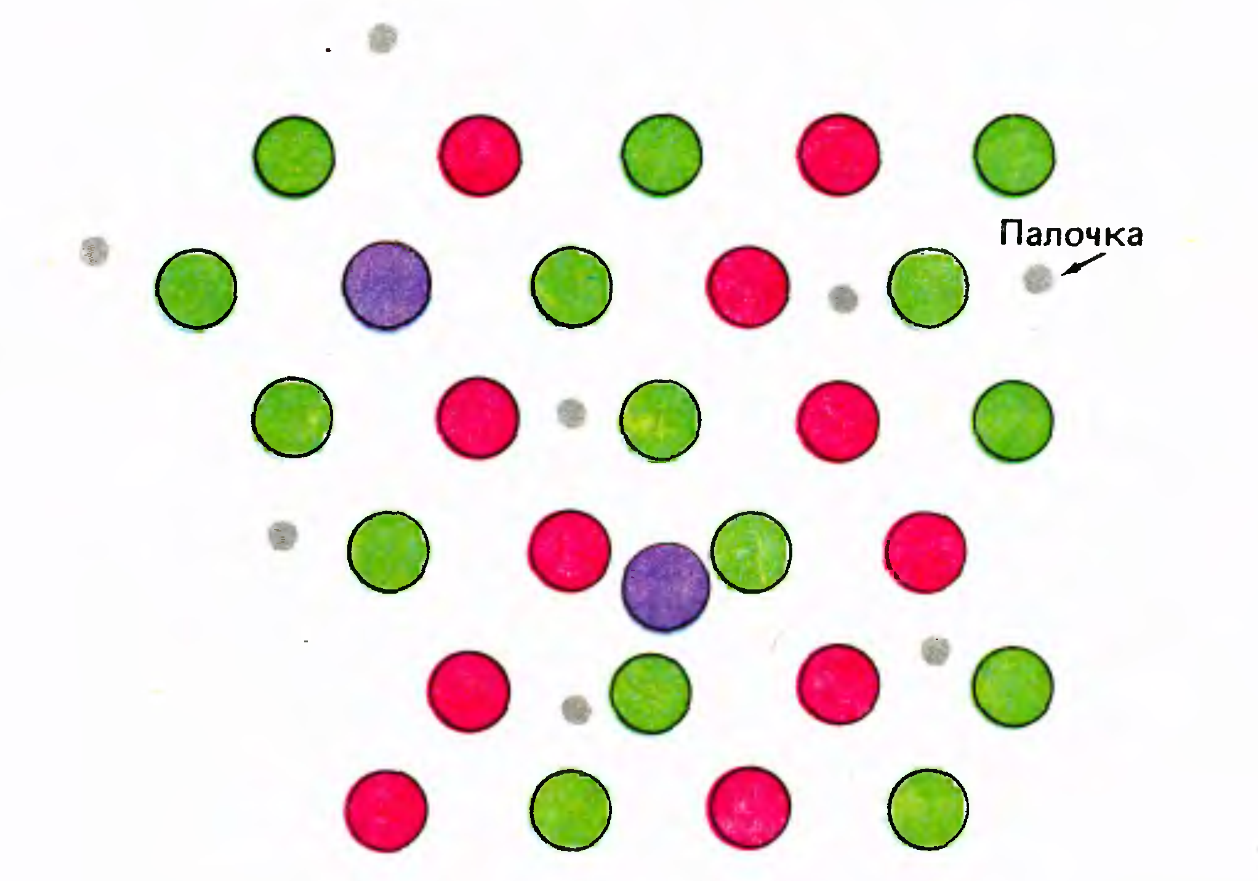
Distribution of color cones in the central fossa of the eye (David Hubel "Eye, brain, vision")

The spectral composition of light is a description of its intensity at different frequencies. Illumination of any area of ​​the retina causes the response of rods and cones located in this area. The nature of the response of the cones depends on the spectral characteristics of the incident light and the type of cones themselves. Signals cones are gradual. Joint processing of signals from several cones with different color preferences serves as the basis for the formation of the response of the corresponding ganglion cell.


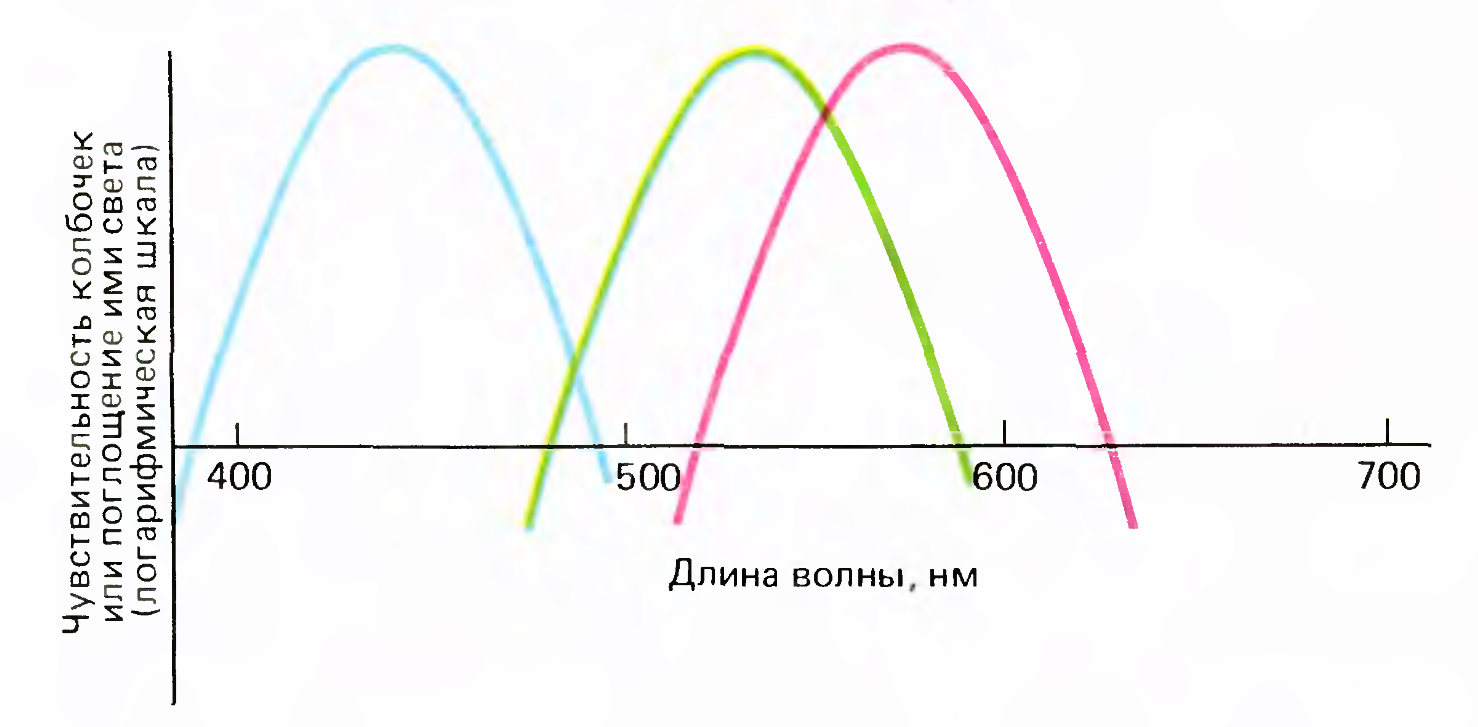
Three types of cone sensitivity

The cones themselves are divided into only three fixed types according to their spectral sensitivity (picture above). But due to the addition of cone signals in different proportions, it is possible to obtain various characteristics of the spectral sensitivity of ganglion cells.

If the light source is monochrome, then the ganglion cell's sensitivity to color can be described by the frequency range of the light that causes the cell to respond. If the spectrum of light has a complex shape, then, apparently, we can talk about a certain integration of the signal in the sensitivity range of the ganglion cell. As a result, it can be assumed that the ganglion cells are detectors that operate in a specific, for each cell, frequency range and amplitude of a conditional monochromatic signal. Then the pattern of activity of the group of compactly located color-sensitive ganglion cells can be sufficiently accurately encode the color in the place of the retina where these cells are located. Such a code will have the properties of Gray codes, that is, a color close in conditional frequency will be encoded with an activity pattern close in its pattern. Such coding is particularly interesting in that it allows not only to transmit information about the color, but also forms an idea of ​​the color sequence. There is a "continuity" of color codes, we get not just a set of colors, but a rainbow in which colors go in a familiar order.

Thus, the same ganglion cells can encode several types of descriptions at once: sharp borders, thin lines and their ends, brightness gradients, fill colors, color gradients.For borders, lines and gradients, the code takes into account not only their place on the retina, but also the angle.

We can assume some optimization in the transmission of such codes along the optic nerve. For example, in order not to lose information when several rather dense codes are superimposed on each other, it is possible to transmit them with a small time offset. Then within the “one frame” one ganglion cell can potentially work several times, which will create a feeling of frequency coding.

The described mechanism allows you to encode and transmit all the details of the image, but miracles do not happen. The ability to compare for the built-in code has to be paid for by some increase in the binary vector. With this in mind, one million nerve fibers coming from one eye is small enough to convey a “good” realistic picture. This is due to the fact that the eye does not transmit the entire picture equally clearly. For ganglion cells lying on the periphery, the size of the receptive fields is ten times the size of the fields in the central fossa. Due to this, we clearly see in a fairly narrow field of view. But due to the fact that the eye constantly makes fast, abrupt movements - saccades, we have the impression of the clarity of the entire visible image.

Place your hand in front of you and focus your vision on your thumb (picture below). You will find that you cannot say how many more fingers are on the same hand. Similarly, if you look at any word on the monitor and fix your eyes on its first letter, then the fourth letter from it will be indistinguishable.


Counting the number of fingers

Sound coding

Similarly, visual information can be encoded and audio information. An ear diagram is shown in the figure below. The sound wave causes oscillations of the eardrum, which, through the system of pits of the middle ear, enter the inner ear, in particular, the cochlea .


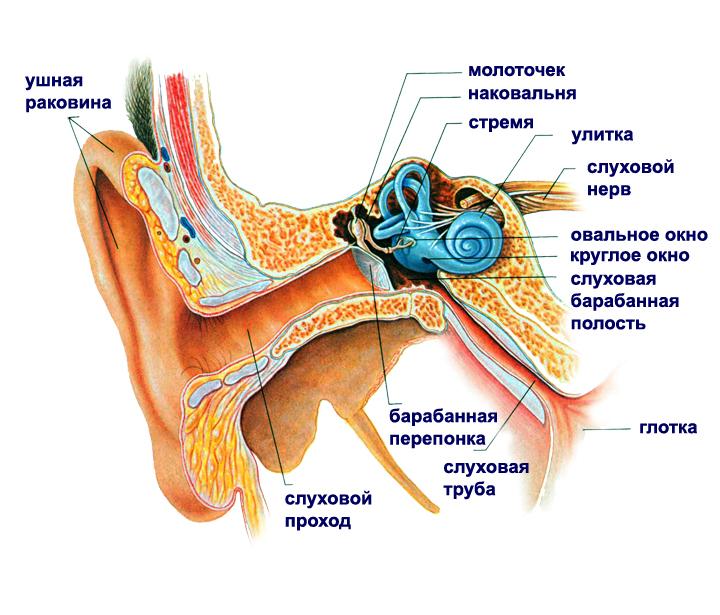
The

snail ear circuit has three spiral channels filled with fluid (figure below). In the middle channel is the organ of Corti .


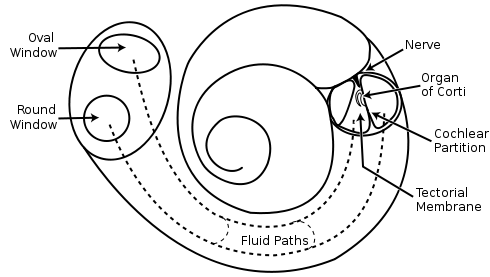
The scheme of the cochlea.

It is clearly visible on the cross section (figure below).



Sensors of the organ of Corti are hair cells. Their hairs cover the surface of the organ of Corti. Fluctuations in the fluid cause hair to vibrate. The intensity of these fluctuations creates the original signals, which are then converted into nerve impulses, which are transmitted further, first through the auditory nerve, and then through the auditory part of the pre-vesicular nerve.

For hearing, the sensory cells of the organ of Corti act as an analogue of cones and rods of the visual retina.

The sound wave causes a traveling wave in the organ of Corti, which begins with a small amplitude at the oval window, reaches a maximum at a specific, frequency-dependent location (picture below), and disappears at the Helicotherm (Bekesy G. Experiments in hearing. New York, etc .: Mc. Grow-Hill Book Co., 1960).


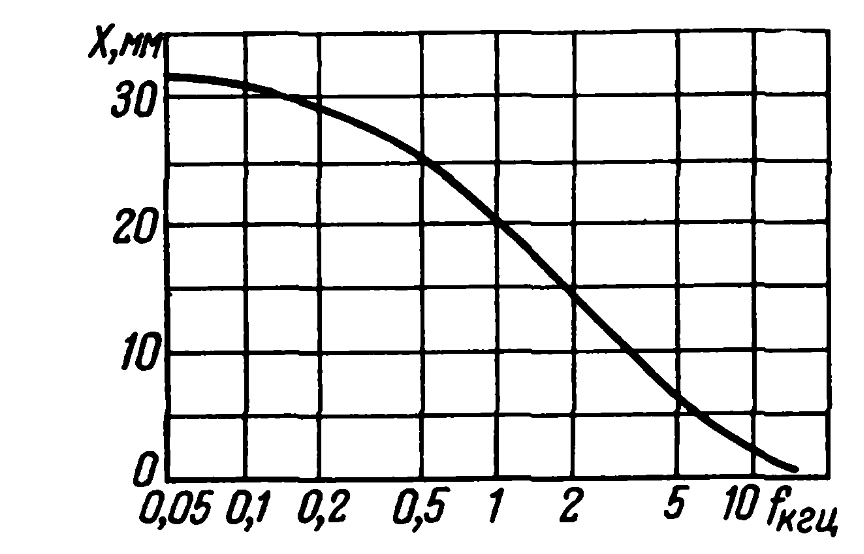
Dependence of the position in the organ of Corti of the place with the maximum amplitude on the frequency (Eberhard Zwicker, Das Ohr als Nachrichtenempfanger, 1967)

With a length of the Corti organ 28 mm, the approximate width of the maximum is 4 mm (Eberhard Zwicker, Das Ohr als Nachrichtenempfanger, 1967). That is, hair-mechanoreceptors work in a fairly wide range of frequencies.

The intensity of the hairs in a certain place in the spiral of the cochlea can be judged on the signal amplitude at this frequency.

It is difficult to say definitely, but it is possible that the shape of the channels and the relative position of the hairs make it possible to judge not only the amplitude, but also the phase of the sound signal at each of the frequencies.

The activity of the hairs of the organ of Corti contains all the information that is needed to represent the original sound signal in the form of its frequency-spectral decomposition.

In order for the hairs to signal not the instantaneous value of their bend, but to reflect more general signal characteristics, a certain temporal integration is necessary. The result is a fairly accurate analogy with the window Fourier transform .

In a small time interval corresponding to the time window, the audio information can be recorded as a set of triplets (frequency, amplitude, phase). This set is the Fourier coefficients of the decomposition and allows you to restore the original signal.

Now, if we introduce a sufficient set of “wide” detectors that operate in certain frequency ranges, amplitudes and phases, then the activity of such detectors can accurately transmit information about the original signal spectrum.

This procedure allows you to present the result of a single measurement of the signal spectrum in the form of a binary vector that has the properties of Gray codes described above. That is, the sound sections “similar” in their spectral portrait will be “similar” in their binary code as well. Moreover, similarly with vision, this code will initially contain an idea of ​​the amplitude, phase and frequency sequence of sounds.

From the "instant" description of the spectrum, it is easy to go to a binary description of the time interval of any length. To do this, you need to increase the number of “wide” detectors and enter another parameter - time.

For timing, you will need a ring identifier, which will return to its original state after a certain time interval. This interval will determine the maximum "recording duration".

In the new vector, each bit corresponding to its “wide” detector will be triggered in a certain neighborhood of the point specified by the combination indication (frequency, amplitude, phase, time). The general principle will remain the same. A separate bit will talk about a certain range of values, but a set of bits will give a code that describes the value quite accurately.

This encoding is not much different from image encoding. The time base of the spectrum creates an image where the amplitude corresponds to the brightness. True, the “invisible” phase is also added.

If you depict the spectral picture of the sound, perform the encoding described, and then restore the sound from it and see its picture, then these pictures are expected to be similar (picture below).


The picture of the original sound (above), the picture of the sound restored after binary encoding (below) (Dmitry Kashitsyn)

The sound of the two sound fragments is below. One is the original sound, the other is its recovery after the encoding described.
Original sound.
Restored sound.

Encoding sound "in the forehead" through the detectors (frequency, amplitude, phase, time) is given for example. Evolution inevitably optimized and found an optimal performance for sound. Visual information is not encoded by the eye with a description of the brightness of individual areas, but by boundary codes with their direction, gradients with the direction and degree of the gradient itself, codes of thin lines with their direction and the like. That is, those elements that are most indicative of real pictures and create the optimal basis for the description. Surely, something similar is inherent in the ear. The cunning shape of the cochlear channels and the organ of Corti suggests that hair-detectors respond not only to frequencies, amplitudes and phases, but also to more complex components of the audio signal. For example,on the spectral component of a certain frequency width going upstream or downward in frequency, sounding with increasing or decreasing volume.

The most interesting thing is that coding such complex things is not particularly difficult. It is enough to create detectors, each triggered in a certain range of parameters, everything else will arise by itself. Moreover, the resulting code will have the properties of Gray codes in "all directions" of the signal change. There will be continuity of the code in the direction of frequency, amplitude, phase, time.

Coding features

The described mechanism for obtaining binary codes from image and sound allows you to create a binary description of the source information, the accuracy of which is determined by the “gap width” between the “wide” detectors. That it sets the error of the description.

This encoding is very convenient for comparison between different descriptions. In the description itself, all the necessary information about the proximity of similar objects is encrypted.

We have already talked about the complexity that convolution networks encounter when trying to match two too clear images. The slightest shift leads to the fact that the coincidence is zero (the figure below (left)). To overcome this, the blurring of both images is used, then a small displacement is no longer so critical (the figure below (on the right)).

Blur, in fact, sets for each point the parameters for calculating its proximity to other points. Intersect blurring - there is proximity, do not intersect - no. The radius of the blur can be adjusted the distance over which the idea of ​​proximity.


A single offset results in a complete absence of coincidence (left). A similar situation after blurring gives a significant coincidence (right) (Fukushima K., 2013)

A simple blurring of the image blurs everything at once: the position, angles, gradients, and colors — everything becomes less sharp. The described binary coding allows you to "blur" each of the parameters separately from the others, thereby significantly increasing the meaningfulness of the comparison.

Relation to generalization

Using the example of the retina and the organ of Corti, I wanted to show that there are mechanisms that allow translating any visual or sound image into the space of binary codes such that it not only stores information about the original image, but also the code itself lays down the idea of ​​the proximity structure of the original elements descriptions. In such binary codes there is everything that is required for comparing images, taking into account the degree of closeness of the description elements.

The resulting coding turns out to be multidimensional and takes into account the degree of closeness of the description elements in different dimensions.

If for the initial description to introduce separate concepts, it is easy to get the binary codes of these concepts. At the same time, it turns out that the semantic graph, which takes into account both the closeness of these concepts, and the hierarchy of their mutual occurrence, is completely determined by the resulting system of binary codes. That is, when manipulating such concepts, it is not necessary to separately store or transfer the system of semantic relations - all that is necessary is already in the codes themselves.

When we talked about generalizations, we said that we would like to have a system of generalized concepts not just as a set of independent elements, but as a system that takes into account all the relationships of these generalizations. Further it will be shown that the ideas described in this part of the coding can be used in the mechanism of universal generalization.

About the developers

Retina modeling was performed by shabanovd (Dmitry Shabanov), as part of a project on modeling the visual perception system. Sound coding modeling performed by Halt (Dmitry Kashitsyn).

Alexey Redozubov

. 1.
. 2.
. 3.
. 4.
. 5.
. 6.
. 7.
. « »
. 8.
. 9.
. 10.
. 11.
. 12. .