Complex neural network based on the Fourier series of a function of many variables
There are many tasks for which the direct propagation neural networks with a sigmoidal activation function are not optimal. For example - problems of recognition of binary images, with preprocessing using Fourier transform. During these transformations, the image becomes invariant to offsets, scaling, and rotations. An example of such transformations is given below. [1] At the output, such a method produces a vector of complex numbers. Modern neural networks cannot work with them. they only work with real numbers.
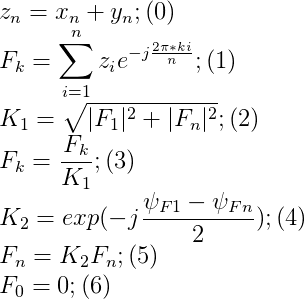
The second such task is the prediction of time series with a given accuracy. Direct propagation networks with a sigmoidal activation function do not make it possible to predict an error in the number of hidden neurons. In order to be able to predict this error, it is worth using some series for the rate of convergence of which there are calculation formulas. Fourier series was chosen as such a series.
')
Fourier series
Complex Fourier series of one variable.

But neural networks often work with functions of many variables. I propose to consider the Fourier series of two independent variables. [2]
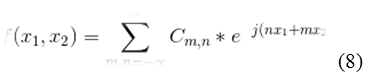
In general, one should use the Fourier series for functions of "k" variables.
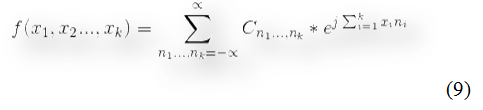
Architecture
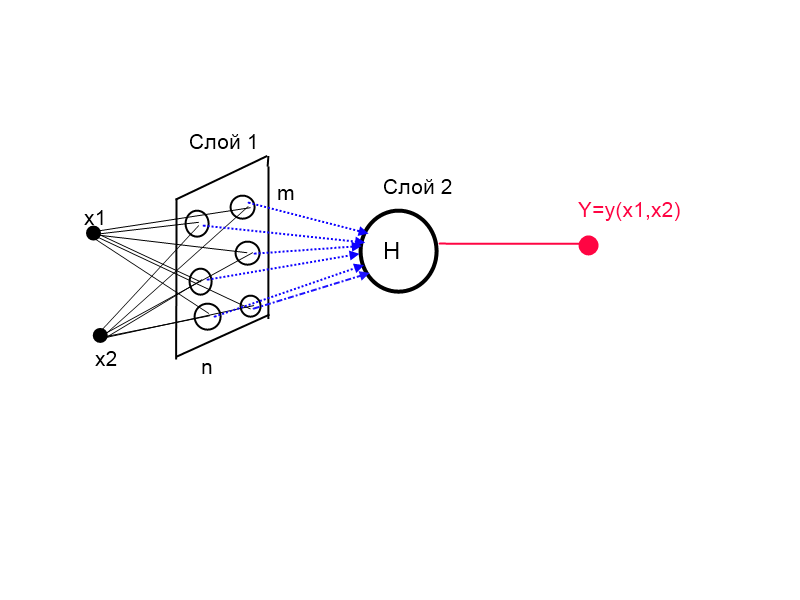
Figure 1. Integrated network architecture (KINSF)
Figure 1 shows the architecture of the complex artificial Fourier neural network (KINSF), which essentially implements formula 9. Here the hidden layer is the mxn neuron matrix where m is the number of Fourier decomposition descriptors and n is the dimension of the input vector. The weights in the first layer have the physical meaning of the frequencies with the highest energy, and the weights of the second layer have the meaning of the coefficients of the Fourier series. Thus, the number of inputs for each neuron of the output layer is m * n, which corresponds to the number of coefficients of the Fourier series.
Figure 2 shows a diagram of a separate neuron of the hidden layer.
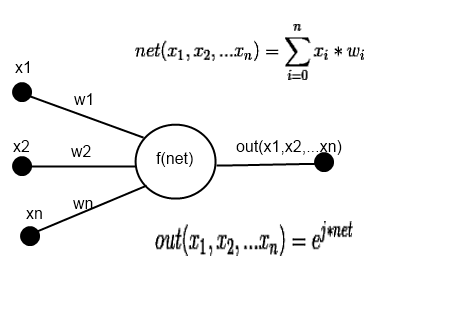
Figure 2. Scheme of the neuron of the hidden layer.
Figure 3 is a diagram of the neuron of the output layer.
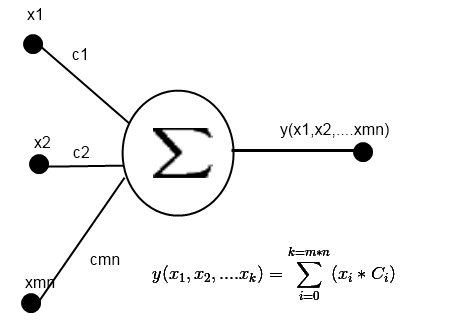
Figure 3. Diagram of the neuron of the output layer.
Architecture optimization
Creating a matrix of neurons involves the use of large computational resources. You can reduce the number of neurons on the hidden layer n times. In this case, each neuron of the hidden layer has n outputs, if we have n inputs in the network, then with this approach the number of connections decreases n square times without losing the quality of approximation of functions. Such a neural network is shown in Figure 4.
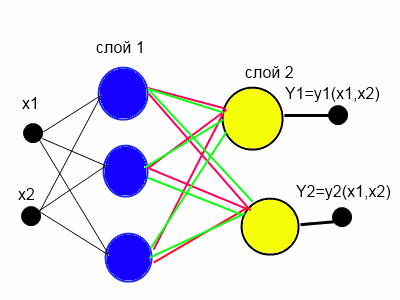
Figure 4. KINSF, the reduction of the matrix into a vector.
The principle of the NA
We write the principle of operation of this NA in matrix form.
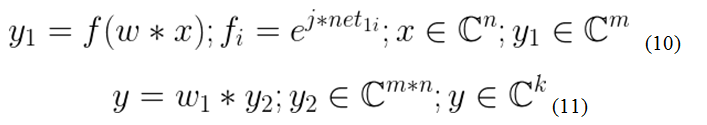
Expression 10 describes the output of the hidden layer, where: n is the dimension of the input “x” vector, m is the dimension of the output vector of the hidden layer “y1”, f is the activation vector function, j is the imaginary unit, w is the weights matrix, net1 = w * x, k is the number of outputs of the NA. Expression 11 in turn shows the operation of the output layer, the vector "y2" is obtained by n-times duplicating the vector y1. In Appendix A, for clarity of implementation methods, a program listing is presented that works on the basis of expressions 10-11.
Reducing the task of learning to the task of learning a single-layer perceptron.
Using the physical meaning of the weights of the neurons of the hidden layer, namely that the weights of the neurons of the hidden layer are frequencies. Assuming that the oscillations are periodic, it is possible to determine the initial cyclic frequencies for each direction, and to initialize the weights in such a way that, passing from a neuron to a neuron, the frequencies will multiply. So you can reduce the task of learning a complex two-layer network to the task of learning a single-layer perceptron. The only difficulty is that the inputs and outputs of this perceptron are complex. But the teaching methods of this network will be discussed in the next article.
KINSF modification for recognition tasks
In problems of recognition or classification at the output of neural networks, it is necessary to obtain the so-called membership function [3], the value of which lies within, from zero to one. To obtain it, it is very convenient to use the logistic sigmoid function (Figure 5). By transforming a few neurons of my network, it is possible to get a network for pattern recognition. Such a network is well suited for recognizing binary images processed by the method described above (expressions 1-6). It takes complex numbers at the input, after which it approximates the function of the image belonging to the class. [4]
Figure 6 shows the neuron of the hidden layer, and figure 7 shows the output layer.
As we can see, the scheme of the hidden neuron has not changed, which cannot be said about the neurons of the output layer.

Figure 6. Scheme of the hidden neuron.

Figure 7. Diagram of the output neuron.
Experiment
For the experiment a number of pictures was chosen, one of them is presented below. Before recognition, binarization and reduction algorithms were used.
Reduction to a general view was performed according to the algorithm presented above (1-6). After that, the vector, in the case of KINSF, was fed completely “as is” to the artificial neural network, and in the case of NS with a sigmaidal activation function, the real and imaginary components were fed separately, after which the vector was recognized. The experiment was conducted using two types of NA. Direct distribution network with sigmoidal activation function and KINSF. The scope of the training sample was 660 vectors divided into 33 classes. The program is shown in Figure 8.

Figure 8. Handwriting recognition software.
The network with a sigmoidal activation function serves separately the real and imaginary components of the complex vector. KINSF and ANN with a sigmoidal activation function were trained using the 500 learning cycles delta rule. As a result of testing, 400 images of KINSF produced an accuracy of 87%, and an ANN with a sigmoidal activation function of 73%.
Code
Video work
Below is a video of the work of this program that was in the test. I wrote it down as a demonstration of how INS can be applied. Immediately apologize for the freestyle presentation.
Results
Benefits:
This network has several advantages. Most importantly, this network can work with complex numbers. It can be used to work with signals specified in a complex form. Also, it is very well suited for recognizing binary images. It can approximate a function, leaving all the properties of the Fourier transform, which makes it easy to analyze. After all, the non-analyzability of the work of neural networks leads to the fact that research projects are increasingly being abandoned by them, solving problems by other methods. Also, the physical meaning of the weights will allow using this neural network for the numerical decomposition of the function of many variables in a Fourier series.
Disadvantages:
A significant disadvantage of this neural network is the presence of a large number of connections. Much more than the number of connections of direct distribution networks of the perceptron type.
Further study:
In the course of further work on this neural network, it is planned: to develop more advanced training methods, to prove the convergence of training, to prove the absence of retraining error for any number of neurons on the hidden layer, to build a recurrent neural network based on KINF designed for processing speech and other signals.
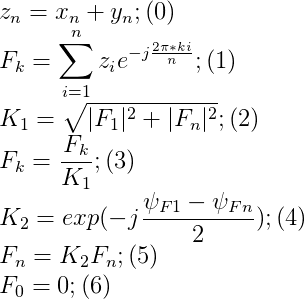
The second such task is the prediction of time series with a given accuracy. Direct propagation networks with a sigmoidal activation function do not make it possible to predict an error in the number of hidden neurons. In order to be able to predict this error, it is worth using some series for the rate of convergence of which there are calculation formulas. Fourier series was chosen as such a series.
')
Fourier series
Complex Fourier series of one variable.

But neural networks often work with functions of many variables. I propose to consider the Fourier series of two independent variables. [2]
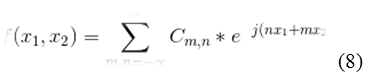
In general, one should use the Fourier series for functions of "k" variables.
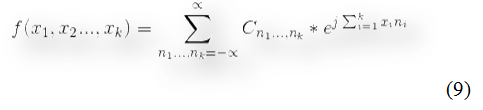
Architecture

Figure 1. Integrated network architecture (KINSF)
Figure 1 shows the architecture of the complex artificial Fourier neural network (KINSF), which essentially implements formula 9. Here the hidden layer is the mxn neuron matrix where m is the number of Fourier decomposition descriptors and n is the dimension of the input vector. The weights in the first layer have the physical meaning of the frequencies with the highest energy, and the weights of the second layer have the meaning of the coefficients of the Fourier series. Thus, the number of inputs for each neuron of the output layer is m * n, which corresponds to the number of coefficients of the Fourier series.
Figure 2 shows a diagram of a separate neuron of the hidden layer.

Figure 2. Scheme of the neuron of the hidden layer.
Figure 3 is a diagram of the neuron of the output layer.

Figure 3. Diagram of the neuron of the output layer.
Architecture optimization
Creating a matrix of neurons involves the use of large computational resources. You can reduce the number of neurons on the hidden layer n times. In this case, each neuron of the hidden layer has n outputs, if we have n inputs in the network, then with this approach the number of connections decreases n square times without losing the quality of approximation of functions. Such a neural network is shown in Figure 4.

Figure 4. KINSF, the reduction of the matrix into a vector.
The principle of the NA
We write the principle of operation of this NA in matrix form.
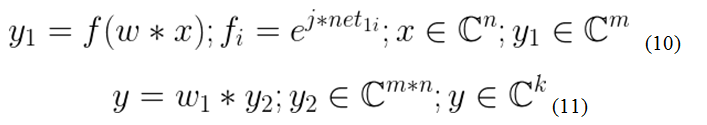
Expression 10 describes the output of the hidden layer, where: n is the dimension of the input “x” vector, m is the dimension of the output vector of the hidden layer “y1”, f is the activation vector function, j is the imaginary unit, w is the weights matrix, net1 = w * x, k is the number of outputs of the NA. Expression 11 in turn shows the operation of the output layer, the vector "y2" is obtained by n-times duplicating the vector y1. In Appendix A, for clarity of implementation methods, a program listing is presented that works on the basis of expressions 10-11.
Reducing the task of learning to the task of learning a single-layer perceptron.
Using the physical meaning of the weights of the neurons of the hidden layer, namely that the weights of the neurons of the hidden layer are frequencies. Assuming that the oscillations are periodic, it is possible to determine the initial cyclic frequencies for each direction, and to initialize the weights in such a way that, passing from a neuron to a neuron, the frequencies will multiply. So you can reduce the task of learning a complex two-layer network to the task of learning a single-layer perceptron. The only difficulty is that the inputs and outputs of this perceptron are complex. But the teaching methods of this network will be discussed in the next article.
KINSF modification for recognition tasks
In problems of recognition or classification at the output of neural networks, it is necessary to obtain the so-called membership function [3], the value of which lies within, from zero to one. To obtain it, it is very convenient to use the logistic sigmoid function (Figure 5). By transforming a few neurons of my network, it is possible to get a network for pattern recognition. Such a network is well suited for recognizing binary images processed by the method described above (expressions 1-6). It takes complex numbers at the input, after which it approximates the function of the image belonging to the class. [4]
Figure 6 shows the neuron of the hidden layer, and figure 7 shows the output layer.
As we can see, the scheme of the hidden neuron has not changed, which cannot be said about the neurons of the output layer.

Figure 6. Scheme of the hidden neuron.

Figure 7. Diagram of the output neuron.
Experiment
For the experiment a number of pictures was chosen, one of them is presented below. Before recognition, binarization and reduction algorithms were used.
Reduction to a general view was performed according to the algorithm presented above (1-6). After that, the vector, in the case of KINSF, was fed completely “as is” to the artificial neural network, and in the case of NS with a sigmaidal activation function, the real and imaginary components were fed separately, after which the vector was recognized. The experiment was conducted using two types of NA. Direct distribution network with sigmoidal activation function and KINSF. The scope of the training sample was 660 vectors divided into 33 classes. The program is shown in Figure 8.

Figure 8. Handwriting recognition software.
The network with a sigmoidal activation function serves separately the real and imaginary components of the complex vector. KINSF and ANN with a sigmoidal activation function were trained using the 500 learning cycles delta rule. As a result of testing, 400 images of KINSF produced an accuracy of 87%, and an ANN with a sigmoidal activation function of 73%.
Code
public class KINSF_Simple { ComplexVector input; // ComplexVector output, // fOut; // Matrix fL; // ComplexMatrix C; // int inpN, outpN, hN, n =0 ; Complex J = new Complex(0,1); // public KINSF_Simple(int inpCout, int outpCout, int hLCount) { inpN = inpCout; outpN = outpCout; hN = hLCount; // . fL = Statistic.rand(inpN, hN); C = Statistic.randComplex(inpN*hN,outpN); } /// <summary> /// - /// </summary> /// <param name="compVect"></param> /// <returns></returns> public ComplexVector FActiv1(ComplexVector compVect) { ComplexVector outp = compVect.Copy(); for(int i = 0; i<outp.N; i++) { outp.Vecktor[i] = Complex.Exp(J*outp.Vecktor[i]); } return outp; } /// <summary> /// /// </summary> /// <param name="inp"></param> void OutputFirstLayer(ComplexVector inp) { input = inp; fOut = FActiv1(inp*fL); } /// <summary> /// /// </summary> void OutputOutLayer() { List<Complex> outList = new List<Complex>(); for(int i = 0; i<inpN; i++) { outList.AddRange(fOut.Vecktor); } ComplexVector outVector = new ComplexVector(outList.ToArray()); output = fOut*C; } /// <summary> /// /// </summary> /// <param name="inp"> </param> /// <returns></returns> public ComplexVector NetworkOut(ComplexVector inp) { OutputFirstLayer(inp); OutputOutLayer(); return output; } } Video work
Below is a video of the work of this program that was in the test. I wrote it down as a demonstration of how INS can be applied. Immediately apologize for the freestyle presentation.
Results
Benefits:
This network has several advantages. Most importantly, this network can work with complex numbers. It can be used to work with signals specified in a complex form. Also, it is very well suited for recognizing binary images. It can approximate a function, leaving all the properties of the Fourier transform, which makes it easy to analyze. After all, the non-analyzability of the work of neural networks leads to the fact that research projects are increasingly being abandoned by them, solving problems by other methods. Also, the physical meaning of the weights will allow using this neural network for the numerical decomposition of the function of many variables in a Fourier series.
Disadvantages:
A significant disadvantage of this neural network is the presence of a large number of connections. Much more than the number of connections of direct distribution networks of the perceptron type.
Further study:
In the course of further work on this neural network, it is planned: to develop more advanced training methods, to prove the convergence of training, to prove the absence of retraining error for any number of neurons on the hidden layer, to build a recurrent neural network based on KINF designed for processing speech and other signals.
Literature
1. Osovsky C ... Neural networks for information processing / Per. from Polish I.D. Rudinsky - Moscow: Finance and Statistics, 2004.
2. Fichtengolts G.M. Course of differential and integral calculus. Volume 3. - M .: FIZMATLIT, 2001.
3. Zade L. The concept of a linguistic variable and its application to making approximate decisions. - M .: Mir, 1976.
4. Rutkovskaya D., Pilinsky M., Rutkovsky L. Neural networks, genetic algorithms and fuzzy systems: Trans. from polish I.D. Rudinsky. - M .: Hotline - Telecom, 2006.
2. Fichtengolts G.M. Course of differential and integral calculus. Volume 3. - M .: FIZMATLIT, 2001.
3. Zade L. The concept of a linguistic variable and its application to making approximate decisions. - M .: Mir, 1976.
4. Rutkovskaya D., Pilinsky M., Rutkovsky L. Neural networks, genetic algorithms and fuzzy systems: Trans. from polish I.D. Rudinsky. - M .: Hotline - Telecom, 2006.
Source: https://habr.com/ru/post/321066/
All Articles