Budget version of TrueRMS measurement
Introduction
Measuring trueRMS AC voltage is not an easy task, not what it seems at first glance. First of all, because most often you have to measure not purely sinusoidal voltage, but something more complex, complicated by the presence of harmonics of noise.
Therefore, a seductively simple solution with a mean value detector recounted in cf. Values do not work where the waveform is very different from sinusoidal or simply unknown.
')
Professional voltmeters cf. sq. Values are quite complex devices both in circuit design and algorithms [1, 2]. In the majority of meters that are of an auxiliary nature and serve to control the operation, such complexity and accuracy are not required.
It also requires that the meter be built on the simplest 8-bit microcontroller.
General measurement principle
Let there be some kind of alternating voltage of the type shown in fig. one.
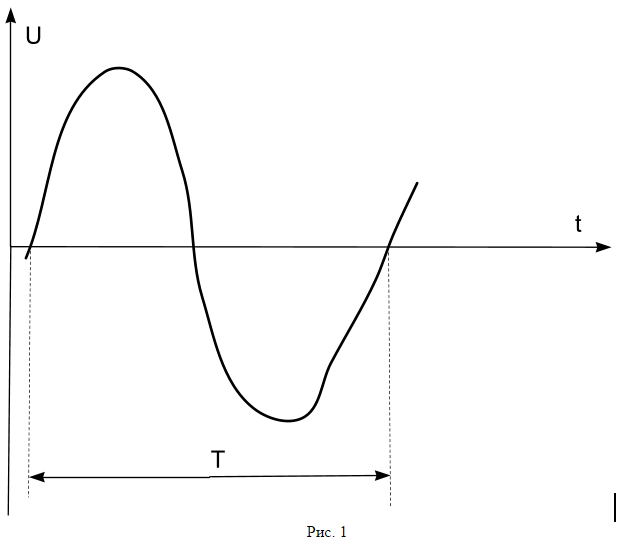
Quasi-sinusoidal stress has a certain quasi-period T.
The advantage of measuring the rms voltage is that, in general, the measurement time does not play a big role, it only affects the frequency band of the measurement. More time gives more averaging, less gives an opportunity to see short-term changes.
The basic definition is cf. sq. values looks like this:
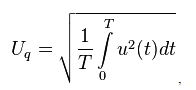
where u (t) is the instantaneous voltage value
T - measurement period
Thus, the measurement time can be, generally speaking, any.
For a real measurement with a real instrument for calculating the integrand expression, it is necessary to quantize a signal with a certain frequency, obviously exceeding at least 10 times the frequency of the quasi-sinusoid. When measuring signals with frequencies within 20 kHz, this is not a problem even for 8-bit microcontrollers.
Another thing is that all standard controllers have unipolar power. Therefore, to measure the instantaneous alternating voltage at the time of the negative half-wave is not possible.
In [3], a rather ingenious solution was proposed for how to introduce a constant component into a signal. At the same time, in that decision, determining the moment when it is necessary to begin or end the process of calculating the mean. sq. The values seem rather cumbersome.
In this paper, we propose a method for overcoming this drawback, as well as calculating the integral with greater accuracy, which makes it possible to reduce the number of sample points to a minimum.
Features of the analog part of the meter
In fig. 2 shows the core of the pre-analog signal processing circuit.
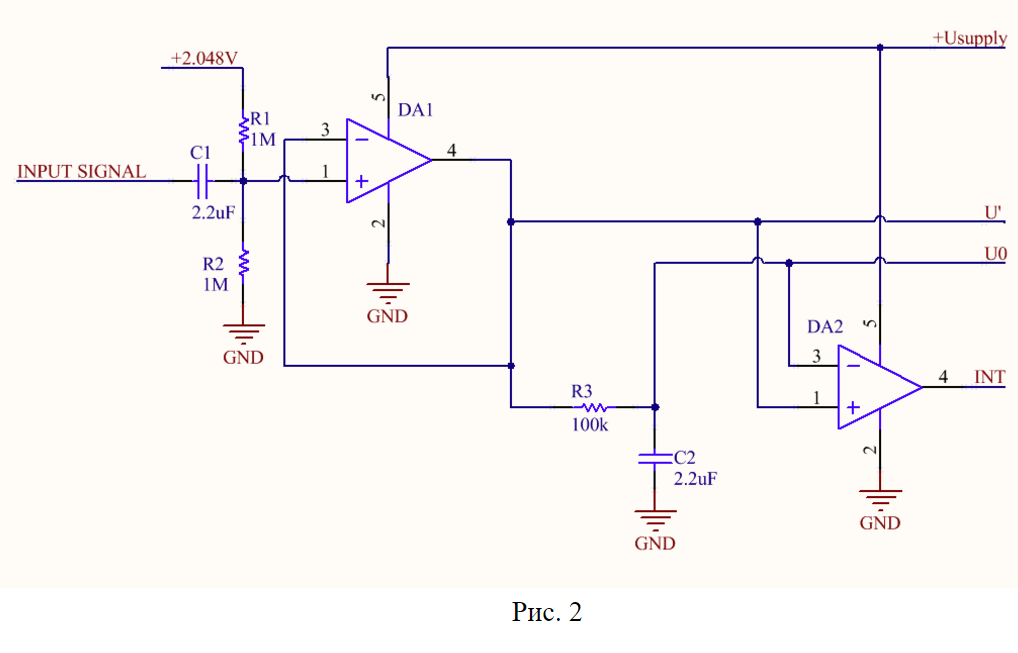
The signal enters through the capacitor C1 to the amplifier-shaper, assembled on the operational amplifier DA1. The ac voltage signal is mixed at the non-inverting input of the amplifier with half the reference voltage, which is used in the ADC. The voltage is chosen to be 2.048 V, since in compact devices the supply voltage is often +3.6 V or less. In other cases, it is convenient to use 4.048 V, as in [3].
From the output of the amplifier-shaper through the integrating chain R3-C2 signal is fed to the input of the ADC, which serves to measure the constant component of the signal (U0). From the amplifier-driver, the signal U 'is a measured signal shifted by half of the reference voltage. Thus, to obtain the variable component, it suffices to calculate the difference U'-U0.
The signal U0 is also used as a reference for the comparator DA2. When U 'goes over U0, the comparator produces a differential, which is used to form an interruption procedure for collecting measurement samples.
It is important that in many modern microcontrollers both operational amplifiers and comparators are built in, without mentioning the ADC.
Basic algorithm
In fig. 3 given the basic algorithm for the case of measuring the magnitude of the AC voltage with a fundamental frequency of 50 Hz.
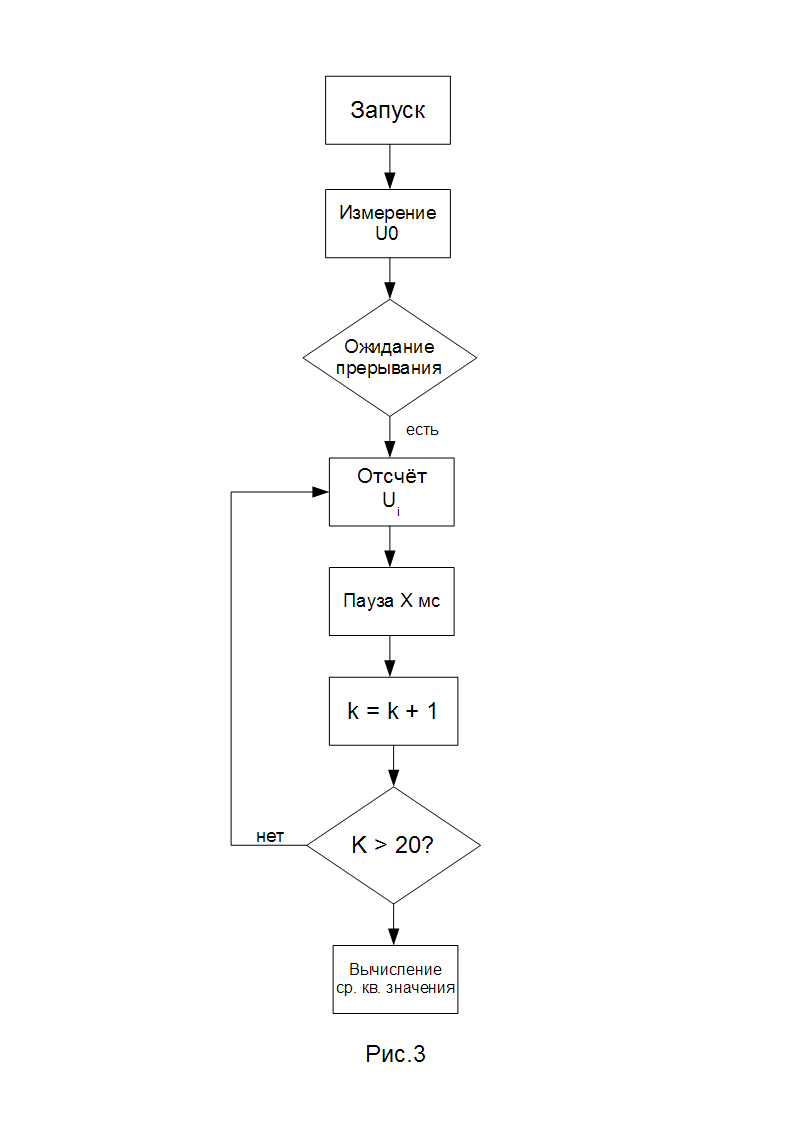
The measurement can be triggered by any external event up to the button that is pressed manually.
After start-up, the constant component in the input signal of the ADC is measured first, and then the controller switches to waiting for a positive differential at the comparator output. As soon as a differential interrupt occurs, the controller makes a sample of 20 points with a time step corresponding to 1/20 of the quasi-period.
The algorithm is written X ms, because the low-cost controller has its own delay time. For the measurement to occur at the right times, this delay must be taken into account. Therefore, the real delay will be less than 1 ms.
In this example, the delay corresponds to measurements of a quasi-sinusoid in the range of 50 Hz, but it can be any, depending on the quasi-period of the measured signal within the speed response of a particular controller.
When measuring sr.kv. the voltage values of an arbitrary quasi-periodic signal, if it is not known a priori what the signal is, it is advisable to measure its period using the timer built into the controller and the same comparator output. And already on the basis of this measurement to establish a delay in the implementation of the sample.
RMS Calculation
After the ADC has created a sample, we have an array of values U '[i], a total of 21 values, including the value U0. Now, if we apply the Simpson formula (more precisely, Cotes) for numerical integration, as the most accurate for this application, we obtain the following expression:
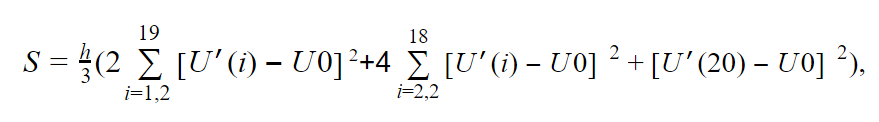
where h is the measurement step, and the zero component of the formula is absent, since it is equal to 0 by definition.
As a result of the calculation, we obtain the value of the integral in its pure form in the ADC sample format. To translate into real values, the obtained value must be scaled according to the magnitude of the reference voltage and divided by the integration time interval.
where Uop is the reference voltage of the ADC.
If everything is recalculated in mV, K is approximately equal to just 2. The scale factor refers to the differences in square brackets. After recalculation and calculation, S is divided by the measurement interval. Taking into account the multiplier h, we actually obtain the division by an integer instead of multiplying by h followed by dividing by the measurement time interval.
And in the final we extract the square root.
And here the most interesting and difficult comes. It is possible, of course, to use a floating point for computations, since the C language allows for even 8-bit controllers, and to perform computations directly using the formulas given. However, the speed of calculation will drop significantly. You can also go beyond the very small RAM of the microcontroller.
To avoid this, it is necessary, as correctly stated in [3], to use a fixed point and operate with a maximum of 16-bit words.
The author managed to solve this problem and measure the voltage with an error Uop / 1024, i.e. for the given example with an accuracy of 2 mV with a total measurement range of ± 500 mV at a supply voltage of +3.3 V, which is enough for many process monitoring tasks.
A software trick is to do all of the division processes, if possible, before the multiplication or exponentiation processes, so that the intermediate result of the operations does not exceed 65535 (or 32768 for actions with a sign).
A specific software solution is beyond the scope of this article.
Conclusion
This article discusses the features of measuring the rms voltage using 8-bit microcontrollers, shows a variant of the circuit implementation and the basic algorithm for obtaining quantization samples of a real quasi-sinusoidal signal.
Links
Measuring trueRMS AC voltage is not an easy task, not what it seems at first glance. First of all, because most often you have to measure not purely sinusoidal voltage, but something more complex, complicated by the presence of harmonics of noise.
Therefore, a seductively simple solution with a mean value detector recounted in cf. Values do not work where the waveform is very different from sinusoidal or simply unknown.
')
Professional voltmeters cf. sq. Values are quite complex devices both in circuit design and algorithms [1, 2]. In the majority of meters that are of an auxiliary nature and serve to control the operation, such complexity and accuracy are not required.
It also requires that the meter be built on the simplest 8-bit microcontroller.
General measurement principle
Let there be some kind of alternating voltage of the type shown in fig. one.
Quasi-sinusoidal stress has a certain quasi-period T.
The advantage of measuring the rms voltage is that, in general, the measurement time does not play a big role, it only affects the frequency band of the measurement. More time gives more averaging, less gives an opportunity to see short-term changes.
The basic definition is cf. sq. values looks like this:
where u (t) is the instantaneous voltage value
T - measurement period
Thus, the measurement time can be, generally speaking, any.
For a real measurement with a real instrument for calculating the integrand expression, it is necessary to quantize a signal with a certain frequency, obviously exceeding at least 10 times the frequency of the quasi-sinusoid. When measuring signals with frequencies within 20 kHz, this is not a problem even for 8-bit microcontrollers.
Another thing is that all standard controllers have unipolar power. Therefore, to measure the instantaneous alternating voltage at the time of the negative half-wave is not possible.
In [3], a rather ingenious solution was proposed for how to introduce a constant component into a signal. At the same time, in that decision, determining the moment when it is necessary to begin or end the process of calculating the mean. sq. The values seem rather cumbersome.
In this paper, we propose a method for overcoming this drawback, as well as calculating the integral with greater accuracy, which makes it possible to reduce the number of sample points to a minimum.
Features of the analog part of the meter
In fig. 2 shows the core of the pre-analog signal processing circuit.
The signal enters through the capacitor C1 to the amplifier-shaper, assembled on the operational amplifier DA1. The ac voltage signal is mixed at the non-inverting input of the amplifier with half the reference voltage, which is used in the ADC. The voltage is chosen to be 2.048 V, since in compact devices the supply voltage is often +3.6 V or less. In other cases, it is convenient to use 4.048 V, as in [3].
From the output of the amplifier-shaper through the integrating chain R3-C2 signal is fed to the input of the ADC, which serves to measure the constant component of the signal (U0). From the amplifier-driver, the signal U 'is a measured signal shifted by half of the reference voltage. Thus, to obtain the variable component, it suffices to calculate the difference U'-U0.
The signal U0 is also used as a reference for the comparator DA2. When U 'goes over U0, the comparator produces a differential, which is used to form an interruption procedure for collecting measurement samples.
It is important that in many modern microcontrollers both operational amplifiers and comparators are built in, without mentioning the ADC.
Basic algorithm
In fig. 3 given the basic algorithm for the case of measuring the magnitude of the AC voltage with a fundamental frequency of 50 Hz.

The measurement can be triggered by any external event up to the button that is pressed manually.
After start-up, the constant component in the input signal of the ADC is measured first, and then the controller switches to waiting for a positive differential at the comparator output. As soon as a differential interrupt occurs, the controller makes a sample of 20 points with a time step corresponding to 1/20 of the quasi-period.
The algorithm is written X ms, because the low-cost controller has its own delay time. For the measurement to occur at the right times, this delay must be taken into account. Therefore, the real delay will be less than 1 ms.
In this example, the delay corresponds to measurements of a quasi-sinusoid in the range of 50 Hz, but it can be any, depending on the quasi-period of the measured signal within the speed response of a particular controller.
When measuring sr.kv. the voltage values of an arbitrary quasi-periodic signal, if it is not known a priori what the signal is, it is advisable to measure its period using the timer built into the controller and the same comparator output. And already on the basis of this measurement to establish a delay in the implementation of the sample.
RMS Calculation
After the ADC has created a sample, we have an array of values U '[i], a total of 21 values, including the value U0. Now, if we apply the Simpson formula (more precisely, Cotes) for numerical integration, as the most accurate for this application, we obtain the following expression:
where h is the measurement step, and the zero component of the formula is absent, since it is equal to 0 by definition.
As a result of the calculation, we obtain the value of the integral in its pure form in the ADC sample format. To translate into real values, the obtained value must be scaled according to the magnitude of the reference voltage and divided by the integration time interval.
where Uop is the reference voltage of the ADC.
If everything is recalculated in mV, K is approximately equal to just 2. The scale factor refers to the differences in square brackets. After recalculation and calculation, S is divided by the measurement interval. Taking into account the multiplier h, we actually obtain the division by an integer instead of multiplying by h followed by dividing by the measurement time interval.
And in the final we extract the square root.
And here the most interesting and difficult comes. It is possible, of course, to use a floating point for computations, since the C language allows for even 8-bit controllers, and to perform computations directly using the formulas given. However, the speed of calculation will drop significantly. You can also go beyond the very small RAM of the microcontroller.
To avoid this, it is necessary, as correctly stated in [3], to use a fixed point and operate with a maximum of 16-bit words.
The author managed to solve this problem and measure the voltage with an error Uop / 1024, i.e. for the given example with an accuracy of 2 mV with a total measurement range of ± 500 mV at a supply voltage of +3.3 V, which is enough for many process monitoring tasks.
A software trick is to do all of the division processes, if possible, before the multiplication or exponentiation processes, so that the intermediate result of the operations does not exceed 65535 (or 32768 for actions with a sign).
A specific software solution is beyond the scope of this article.
Conclusion
This article discusses the features of measuring the rms voltage using 8-bit microcontrollers, shows a variant of the circuit implementation and the basic algorithm for obtaining quantization samples of a real quasi-sinusoidal signal.
Links
Source: https://habr.com/ru/post/321008/
All Articles