The logic of consciousness. Part 10. The task of generalization

In principle, any information system is faced with the same issues. How to collect information? How to interpret it? In what form and how to remember it? How to find patterns in the collected information and in what form to write them? How to respond to incoming information? Each of the questions is important and inextricably linked with the rest. In this cycle we are trying to describe how these issues are solved by our brain. In this part, we will talk about, perhaps, the most mysterious component of thinking - the procedure for finding patterns.

Interaction with the outside world leads to accumulation of experience. If there are any patterns in this experience, they can be isolated and subsequently used. The presence of patterns can be interpreted as the presence of something in common in the memories that make up the experience. Accordingly, the selection of such common entities is called a generalization.

The task of generalization is the key task in all disciplines that are somehow related to data analysis. Mathematical statistics, machine learning, neural networks - it all revolves around the task of generalization. Naturally, the brain did not stand aside and, as we can sometimes observe from our own experience, it also sometimes does a good job with generalization.

Despite the fact that generalization arises always and everywhere the very task of generalization, if we consider it in a general form, it remains rather vague. Depending on the specific situation in which a generalization is required, the formulation of the generalization problem may vary in a very wide range. Different formulations of the problem give rise to very different and sometimes quite dissimilar methods of solution.
')
The variety of approaches to generalization creates the feeling that the procedure of generalization is something collective and that there is apparently no universal procedure of generalization. However, it seems to me that a universal generalization is possible and it is inherent in our brain. As part of the approach described in this cycle, we managed to come up with an amazingly beautiful (at least to me it seems so) algorithm, which includes all the classical variations of the generalization problem. This algorithm not only works well, but the most surprising thing is that it ideally falls on the architecture of biological neural networks, which leads one to believe that, indeed, the real brain works somewhere like that.

Before describing the algorithm of such a universal generalization, let us try to figure out what forms of generalization it is customary to single out and, accordingly, what and why should include a universal approach.

Philosophical-semantic approach to the generalization of concepts

Philosophy deals with semantic constructs. Simply put, it expresses and records its statements in natural language phrases. The philosophical-semantic approach to generalization is as follows. Having concepts combined by a certain species trait requires a transition to a new notion, which gives a broader, but less specific interpretation, free from the species trait.

For example, there is the concept of "wristwatch", which is described as: "time indicator attached to the hand with a strap or bracelet." If we get rid of the species attribute "fixed on the hand ...", we get the generalized concept of "clock", like any instrument that defines time.

In the example with the clock in the very name of the wristwatch contained a hint for generalization. It was enough to drop the extra word and get the desired concept. But this is not a pattern, but a consequence of semantics, built “from the opposite”, when we already know the result of the generalization.

The task of pure generalization

In the formulation of Frank Rosenblatt, the task of pure generalization goes like this: “In an experiment on“ pure generalization ”a brain model or perceptron is required to move from a selective response to one stimulus (say, a square in the left side of the retina) to a similar stimulus that does not activate none of the same sensory endings (the square on the right side of the retina) ”(Rosenblatt, 1962).

The emphasis on “pure” generalization implies the absence of “hints”. If we were shown the square in all possible positions of the retina and given the opportunity to remember all this, then the recognition of the frame would be trivial. But according to the condition, the square was shown to us in one place, and we should recognize it in a completely different one. Convolutional networks solve this problem due to the fact that they initially laid down the rules of "dragging" any shape across the entire space of the retina. By knowing how to “move” an image, they can take a square, seen in one place and “try on” it to all possible positions on the retina.


Search for a pattern in the shape of the letter “T” in different positions of the image (Fukushima K., 2013)

We solve the same problem in our model by creating a space of contexts. The difference from convolutional networks is who goes to whom - “the mountain to Magomed” or “Magomed to the mountain”. In convolutional networks, when analyzing a new image, each previously known image varies in all possible positions and “fits around” to the analyzed image. In the context model, each context transforms (mixes, rotates, scales) the analyzed image as it is prescribed by its rules, and then the “shifted” picture is compared with the “fixed” images known in advance. This, at first glance, a small difference gives the following very strong differences in approaches and their capabilities.

Akin to the pure generalization problem is the invariant representation problem. Having a phenomenon appearing before us in different forms, it is required to invariantly describe these concepts in order to recognize the phenomenon in any of its manifestations.

Classification task

There are many objects. There are pre-defined classes. There is a training set - a set of objects about which it is known to which classes they belong. It is required to construct an algorithm that reasonably assigns any objects from the original set to one of the classes. In mathematical statistics, classification problems are attributed to discriminant analysis tasks.

In machine learning , the classification task is considered a learning task with a teacher. There is a training sample, about which it is known: what stimulus at the entrance leads to what reaction at the exit. It is assumed that the reaction is not accidental, but is determined by some regularity. It is required to build an algorithm that most accurately reproduces this pattern.

The algorithm for solving the classification problem depends on the nature of the input data and the types of derived classes. We discussed the problem of classification in neural networks and how learning with the teacher in our model takes place in the previous section.

Clustering task

Suppose we have a multitude of objects and we know the degree of their similarity to each other, given by the distance matrix. It is required to divide this set into subsets, called clusters, so that each cluster unites similar objects, and the objects of different clusters are very different from each other. Instead of a distance matrix, descriptions of these objects can be given and a way to find the distance between the objects according to these descriptions can be specified.

In machine learning, clustering falls under instruction without a teacher.

Clustering is a very tempting procedure. It is convenient to break up many objects into a relatively small number of classes and subsequently use not original, perhaps cumbersome descriptions, but descriptions through classes. If, when splitting, it is known in advance which signs are important for the problem being solved, then clustering can “focus” on these signs and get classes that are convenient for subsequent decision making.

However, in the general case, the answer to the question about the importance of attributes lies outside the clustering problem. Subsequent training, called reinforcement training, should itself, based on an analysis of how well or not the student’s behavior turned out to be, which attributes are important and which are not. In this case, the “most successful” signs may not be signs from the original descriptions, but already generalized classes taken as signs. But in order to determine the importance of signs, it is necessary that these signs are already present in the description at the time of the training with reinforcement. That is, it turns out that it is not known in advance which signs may be important, but this can only be understood by already having these signs.

In other words, depending on which characteristics of the original description to use and which to ignore during clustering, different class systems are obtained. Some of them are more useful for subsequent purposes, others less. In general, it turns out that it would be good to go through all the possible clustering options in order to understand which of them are most successful for solving a particular problem. Moreover, a completely different clustering system may be successful for solving another problem.

Even if we decide on what to emphasize when clustering, the question of optimal detailing will still remain. The fact is that in the general case there is no a priori information about how many classes the initial set of objects should be divided.

Instead of knowing about the number of classes, you can use a criterion that indicates how precisely all objects should correspond to the created classes. In this case, you can start clustering with a certain initial number of classes and add new classes if there are objects for which no class fits well enough. But the procedure with the addition does not remove the issue of optimality of detail. By setting a low threshold for a class to match an object, large classes are obtained, reflecting the basic patterns. When choosing a high threshold, you get a lot of classes with a small number of objects. These classes take into account small details, but there is no forest behind the trees.

Factor analysis

Suppose that we have a set of objects in which all objects are provided with feature descriptions. Such descriptions can be written with corresponding vectors. Further assume that the signs are of quantitative nature.

It is convenient to center the descriptions, that is, to calculate the average for each attribute and adjust the signs to their average value. This is equivalent to transferring the origin of coordinates to the "center of mass". You can count the correlations between the signs. If we write down the correlation matrix of features and find its own vectors, then these vectors will be a new orthogonal basis in which the original set of objects can be described.

In the basis of the original features, due to their possible correlation, linear patterns were “smeared” between features. In the transition to an orthogonal basis, the internal structure of the patterns begins to appear more clearly. Since the orthogonal basis is determined up to rotation, it is possible to rotate the basis of the eigenvectors so that the directions of the axes best fit the directions along which the data have the greatest scatter.

The eigenvalues ​​corresponding to the eigenvectors show what percentage of the total variance falls on which eigenvector. The eigenvectors that account for the most significant percentage of the variance are called the principal components. It is often convenient to go from the description in the original features to the description in the main components.

Since the main components reflect the most significant linear patterns inherent in the original set, they can be called a definite generalization of the initial data.

The remarkable property of factor analysis is that factors can not only resemble the original signs, but can also turn out to be new unobservable entities.

If we compare the generalizations that are obtained through the classes and which are obtained through the factors, then we can conventionally say that the classes distinguish "areas", and factors - "directions".

Often, to assign an object to a class, they look not so much at the proximity of the object to the center of the class, but at the correspondence of the object to the distribution parameters typical of the class (for example, the EM algorithm is built on this). That is, if there is a prison in the suburbs of the city, then the person you will encounter next to the prison is most likely a city dweller, and not a prisoner, although the distance to the city center is much higher than to the prison center. "Areas" should be understood in the light of this observation.

Below is a picture by which you can roughly relate the generalization of classes and factors.


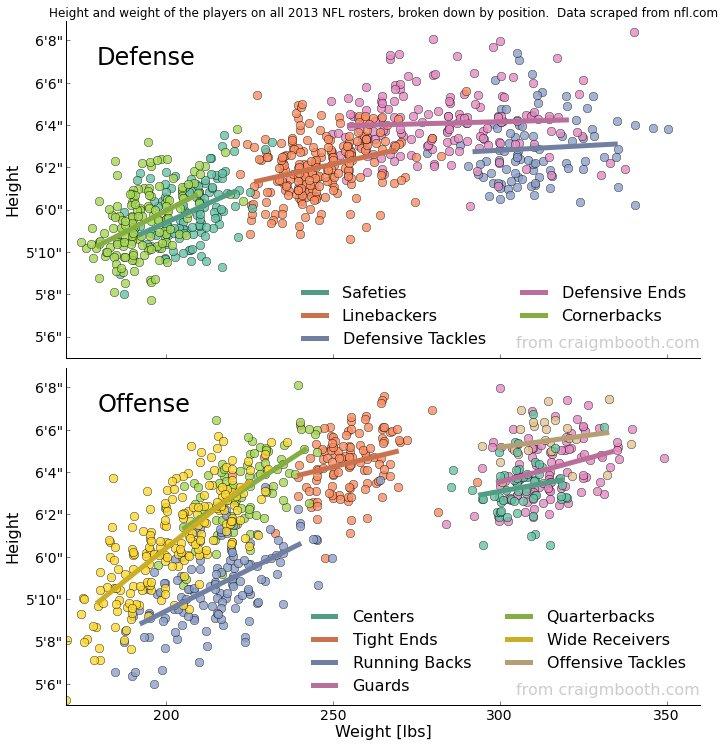
Graphs of the height and weight distribution of players in the American Football League (NFL). Top defense players, bottom attack players. The colors indicate the positions of the players (Dr. Craig M. Booth).

All the many players can be divided into classes according to their role on the field. The parameters "weight - height" can be distinguished global factors (not shown) or factors for each of the classes.

Colored lines correspond to the first major factor in each of the classes. This factor can be interpreted as “player size”. It is defined as the projection of the player’s point on this axis. The value of the projection gives a value that casts off the player’s “non-ideality”. If a second orthogonal axis is drawn to the first axis, then it will describe the second factor “body type”, in other words, a thin player or a fat one.

With all the beauty and convenience of factors, there are also difficulties with them. Just as with classes, there is always the question of how much and what factors should be allocated and used. Of course, it is convenient when the first few main components carry almost all the information, but in practice this happens infrequently. For example, take the 10,000 most popular films, several million people, and analyze the estimates they gave to the films they watched. It is easy to create a correlation matrix for films. The positive correlation between the two films suggests that people who rate one film above the average are likely above the average and the other.

We will conduct a factor analysis of the correlation matrix and then rotation of the axes for easy interpretation of the factors. It turns out that the first five or six factors play a significant role. They correspond to the most common patterns. These, of course, are genres of films: “action”, “comedy”, “melodrama”. In addition, factors will stand out: “Russian cinema” (if people are from Russia) and “author cinema”. The following factors can also be interpreted, but their contribution to the explanation of the variance will be less and less.

The first five most significant factors account for about 30 percent of the total variance. This is not very much, given that the variance is the square of the standard deviation. Accordingly, the main factors account for only 17 percent of the total range of estimates. If you look at the other factors, many of them explain only tenths or hundredths of a percent of the total variance and seem to be insignificant.

But each small factor, as a rule, corresponds to a certain local pattern. He combines films of one director, one screenwriter or one actor. It turns out that when we want to understand something about a particular film, the main factors explain their 30 percent of the variance and at the same time, 40-50 percent of the variance explain one or two small factors that are insignificant for the total mass, but turn out to be extremely important for that the movie.

It is customary to say that "the devil is in the details." This refers to the fact that there are practically no factors that can be neglected. Every little thing can be decisive in a particular situation.

Concept formation

The result of the generalization may be the formation of concepts with the use of which the subsequent descriptions are constructed. There are different opinions on what is the basic principle by which a person selects certain concepts. Actually, all items of this listing are directly related to this.

Idealization task

In the process of generalization, we get concepts that, for some signs, unite a multitude of phenomena that we have previously encountered. The selection of the general that is in these phenomena leads to the fact that we can describe the properties of some ideal concepts, free from the individual details of individual phenomena.

It is ideal concepts that underlie mathematics. Point, line, plane, number, set - these are idealizations of objects from our everyday experience. Mathematics introduces for these concepts a formal system of rules that allows you to build statements, transform these statements, prove or disprove their truth. But if for the mathematics itself the basic concepts are primary, then for man they are connected with the experience of using them. This allows mathematicians not to use complete exhaustive search for evidence, but to carry out a more focused search, based on the experience behind ideal concepts.

Logical induction

Logical induction involves obtaining a general law in a multitude of particular cases.

Share full induction:

The set A consists of the elements: A ₁ , A ₂ , A ₃ , ..., A _n .

• A ₁ has the sign B
  
• A ₂ has the sign B
  
• All elements from A ₃ to A _n also have the sign B

Consequently, all elements of the set A have the sign B.

And incomplete induction:

The set A consists of the elements: A ₁ , A ₂ , A ₃ , ..., A _n .

• A ₁ has the sign B
  
• A ₂ has the sign B
  
• All elements from A ₃ to A _k also have a sign B

Therefore, it is likely that A _{k + 1} and the remaining elements of the set A have the sign B.

Incomplete induction deals with probability and may be erroneous ( induction problem ).

Induction is connected with generalization in two points. First, when it is a question of a multitude of objects, it is implied that previously something served as the basis for combining these objects into a single set. That is, there were some mechanisms that allowed us to make a preliminary synthesis.

Secondly, if by the method of induction we find a certain characteristic that is characteristic of elements of a certain group that describes a certain concept, then we can use this characteristic as characterizing it for assignment to this group.

For example, we find that there are mechanical devices with a distinctive dial and hands. According to the external similarity, we make a generalization and attribute them to the class of watches, and form the corresponding concept.

Next we notice that the clock can tell time. This allows us to do incomplete induction. We conclude that the property of all watches is the ability to determine time.

Now we can take the next step of generalization. We can say that everything that allows you to track time can be attributed to the “clock”. Now for hours we can call the sun, which measures the day and school calls, counting the lessons.

Logical induction has much in common with semantic generalization of concepts. But semantic generalization makes a slightly different emphasis. The semantic approach speaks of the signs that make up the description of the concept, and the possibility of discarding their parts to obtain a more general formulation. At the same time, the question remains - where should such definitions of concepts come from, which will make it possible to make the transition to a generalization “through dropping”. Incomplete logical induction just shows the way of the formation of such descriptive signs.

Discretization task

When dealing with continuous values, it is often required to go to their description in discrete values. For each continuous variable, the choice of quantization step is determined by the accuracy of the description that you want to keep. The resulting fragmentation intervals combine different values ​​of a continuous value, matching certain discrete concepts to them. This procedure can be attributed to a generalization of the fact that the union of values ​​occurs on the basis of their falling into the quantization interval, which speaks of their definite generality.

Correlation of concepts

Carrying out a generalization in any possible way, we can present the result of a generalization through a system of concepts. In this case, generalized concepts do not simply form a set of elements independent of each other, but acquire an internal structure of relationships.

For example, the classes obtained as a result of clustering form a spatial structure in which some classes are closer to each other, some further.

When using the description of something through the factors use a set of factor weights. Factor weights take real values. These values ​​can be approximated by a set of discrete concepts. At the same time for these discrete concepts will be characterized by a system of relations "more - less."

Thus, each time we are interested not only in the identification of generalizations, but also in the formation of a certain system, in which it will be clear how these generalizations relate to all other generalizations.

Something similar situation arises in the analysis of natural language. Words of a language have certain interrelations. The nature of these relationships may be different. You can talk about the frequency of joint manifestation of words in real texts. You can talk about the similarity of their meanings. You can build a system of relationships based on transitions to more general content. Such constructions lead to semantic networks of different types.


An example of a semantic network (Author: Znanibus - own work, CC BY-SA 3.0, commons.wikimedia.org/w/index.php?curid=11912245 )

It is said that the correct formulation of the problem contains three quarters of the correct answer. It seems that this is also true for the problem of generalization. What do we want to see the result of generalization? Resistant classes? But where are the boundaries of these classes? Factors? What and how much? Patterns? Rare but strong coincidences or fuzzy, but supported by a large number of dependency examples? If we have accumulated data and generalized, then how to choose from a variety of possible concepts those that are best suited to describe a particular situation? What is generalization? What does the generalization correlation system look like?

Next, I will try to give both the "correct" formulation of the problem and a possible answer, supported by working code. But it will be through the article. So far, in the next part, we have to get acquainted with one very important biological hint, which gives, perhaps, the main key to understanding the mechanism of generalization.

Alexey Redozubov

The logic of consciousness. Part 1. Waves in the cellular automaton
The logic of consciousness. Part 2. Dendritic waves
The logic of consciousness. Part 3. Holographic memory in a cellular automaton
The logic of consciousness. Part 4. The secret of brain memory
The logic of consciousness. Part 5. The semantic approach to the analysis of information
The logic of consciousness. Part 6. The cerebral cortex as a space for calculating meanings.
The logic of consciousness. Part 7. Self-organization of the context space
The logic of consciousness. Explanation "on the fingers"
The logic of consciousness. Part 8. Spatial maps of the cerebral cortex
The logic of consciousness. Part 9. Artificial neural networks and minicolumns of the real cortex.
The logic of consciousness. Part 10. The task of generalization
The logic of consciousness. Part 11. Natural coding of visual and sound information
The logic of consciousness. Part 12. The search for patterns. Combinatorial space