Geekly Articles each Day
📜 ⬆️ ⬇️

The practice of metaprogramming in C ++: binary search tree at compile time

The creators of templates in C ++ laid the foundation for a whole direction for research and development: it turned out that the C ++ template language has Turing completeness , that is, metaprograms (programs designed to work at the compilation stage) C ++ is able to calculate everything computable . In practice, the power of templates is most often used in the description of generalized data structures and algorithms: STL ( Standard Template Library ) is a living example.

However, with the advent of C ++ 11 with its variadic patterns, type_traits library, tuples and constexpr 's, metaprogramming has become more convenient and visual, opening the way to the realization of many ideas that previously could be implemented only with the help of extensions of a specific compiler or complex multi-storeyed macros.

In this article, we will develop an implementation of a binary tree of compile-time lookup: a data structure that is a logical "extension" of a tuple. We will implement a binary tree in the form of a template and practice metaprogramming: transferring recursive and not only algorithms to the C ++ pattern language.

Content



Some theory


To begin with, let's recall some definitions and concepts about data structures and algorithms. You can skip this section and go directly to the implementation details if the reader is familiar with the basics of graph theory and / or represents what binary trees are and how they can be prepared.
')
Definitions and not only:
A free tree (a tree without a selected root) or simply a tree is an acyclic undirected graph.

A tree with a root is a free tree in which one vertex is identified, called the root .

The nodes are the nodes of the tree with the root.

The parent node or parent of node X is the last node preceding X on the path from the root R to this node X. In this case, the node X is called a child of the described parent node Y. The root of the tree has no parent.

A leaf is a node that has no child nodes.

The internal node is a node that is not a leaf.

The degree of node X is the number of child nodes of this node X.

The node depth X is the length of the path from the root R to this node X.

The height of the node (height) - the length of the longest simple (no returns) downward path from node to sheet.

The height of the tree - the height of the root of this tree.

An ordered tree is a tree with a root in which the child nodes of each node are ordered (that is, the set of child nodes is mapped to the set of natural numbers from 1 to k , where k is the total number of child nodes of this node). In simple words, each child node is given a name: “first”, “second”, ..., “ k -th”.

A binary tree (binary tree) is ( recursively ) either an empty set (does not contain nodes), or consists of three disjoint sets of nodes: the root node , the binary tree, called the left subtree , and the binary tree, called the right subtree . Thus, a binary tree is an ordered tree, in which each node has degree no more than 2 and has “left” and / or / or “right” child nodes.

A full binary tree is a binary tree, in which each node is either a leaf or has a power of two. A fully binary tree can be obtained from a binary by adding dummy daughter sheets to each node of degree 1.

A binary search tree is a related data structure implemented through a binary tree, each node of which can be represented by an object containing a key (key) and related data, links to the left and right subtrees and a link to the parent node. The keys of a binary search tree satisfy the property of a binary search tree :
if X is a node and Y is in the left subtree of X , then Y.key ≤ X.key . If the node Y is in the right subtree of X , then X.key ≤ Y.key .
It is understood that we are able to compare keys (a transitive order relation is set on a set of key values, that is, simply speaking, the operation is “less”) and to talk about equality of keys. In the implementation without loss of generality, we will operate with strict order inequalities, using only the operation "<" and "==", built on its basis from the relation
x = y \; \ Leftrightarrow \; \ ;! (x <y) \: \ & \ :! (y <x)

Traversing a tree — forming a list of nodes; the order is determined by the type of traversal.

Warm-up: tuple operations and turning a number into a class


Before plunging into recursive jungle and enjoying the rampage of angle brackets, let's practice writing metafunctions. Next, we need the concatenation functions of tuples and the function of adding a type to an existing tuple:

 template <class U, class V> struct tuple_concat; template <class Tuple, class T> struct tuple_push;

About type operations:
Of course, there is no talk of any "concatenation" and "addition" of types in "type containers". This is a common and important feature of the compile-time world: a certain type (class) cannot be modified in any way, but it is possible to define a new (or among the previously defined, select an existing) type that has the properties we need.

The C ++ 11 standard introduces a type_traits header file (as part of a type support library) containing a collection of useful meta-functions. All of them are patterns of structures, and after instantiation, they locally define some type or a numeric value constant (or nothing, as in the case of disconnecting the overload using std::enable_if ). We will adhere to the same design principles of meta-functions.

The first function accepts two tuples as arguments of the template, the second - a tuple and the type that must be added to the tuple. The substitution of unsuitable types as arguments (for example, when attempting to concatenate int and float ) is a meaningless operation, so the basic pattern of these structures is not defined (this will prevent it from being instantiated for arbitrary types), and all the useful work is done in partial specializations :

 template <template <class...> class T, class... Alist, class... Blist> struct tuple_concat<T<Alist...>, T<Blist...>> { using type = T<Alist..., Blist...>; }; template <template <class...> class Tuple, class... Args, class T> struct tuple_push<Tuple<Args...>,T> { using type = Tuple<Args..., T>; };

An approximate translation into the human language specialization tuple_concat :

If the template arguments are two classes that in turn are the results of instantiating the same class template ( T ) with a variable number of arguments, and they were instantiated with the Alist and Blist parameter Blist , then locally define the pseudonym type as instantiated the version of the same template of class T with a concatenated list of arguments, i.e. T<Alist..., Blist...> .

About terminology:
Later in the article, the concepts of “instantiating the template structure of metafunction” (more correct and more sophisticated) and “calling metafunction” (shorter and clearer) will often be identified, essentially meaning the same thing: “in this place of the program from the template, the structure will be generated with all the ensuing the consequences: it will become large, pseudonyms and classes will be defined inside, etc. etc."

It sounds ominous, but in practice everything is simpler than it seems: when you try to call tuple_concat with two tuples of the same type (for example, with two std::tuple ), the type of the same tuple with the “stitched” list of arguments of the input tuples is determined inside the structure. Other instantiations of instantiation are simply not compiled (the compiler will not be able to infer types for the partial specialization defined above, and instantiating a common pattern will be impossible due to the absence of its body). Example:

 using t1 = std::tuple<char,int>; using t2 = std::tuple<float,double>; using t3 = std::tuple<char,int,float,double>; using conc = typename tuple_concat<t1,t2>::type; // using err = typename tuple_concat<int,bool>::type; //  static_assert(std::is_same<t3,conc>::value, ""); //  ,

In the light of the above, consideration of the tuple_push specialization tuple_push not be a big deal. Additionally, for convenience, we define the corresponding template aliases :

 template <typename U, typename V> using tuple_concat_t = typename tuple_concat<U,V>::type; template <typename Tuple, typename T> using tuple_push_t = typename tuple_push<Tuple,T>::type;

This convenient feature appeared in the language in the C ++ 11 standard: for example, it allows you to simply typename tuple_concat<t1,t2>::type tuple_concat_t<t1,t2> to access type instead of the typename tuple_concat<t1,t2>::type .

About concatenation:
The standard tuple header contains a definition (not a meta-) of the tuple_cat() ) function, which constructs a tuple by concatenating an unspecified number of std::tuple 'passed to it as arguments. An attentive reader may notice that tuple_concat can be more easily implemented by outputting the result type decltype(tuple_cat(...)) , however, firstly, the implementation obtained above is not limited to the type of the std::tuple , and secondly, it was warm-up exercise for the gradual immersion in more complex type arithmetic.

Last preparations: not for business, but for the soul of debug, we will learn to turn whole numbers into types : you need to store something in the nodes of the tree, but what could be simpler and more convenient for debugging than storing ordinary numbers in them? But since the tree is not simple, but with types (and compile time), then the numbers should be difficult. In fact, the implementation is extremely simple and well known:

 /// - STL-like  template<size_t number> struct num_t : std::integral_constant<size_t, number> {}; //      template<size_t number> struct num_t { enum : size_t { value = number } };

The meaning of both definitions is the same: instantiating a template with different numerical arguments will lead to the definition of different types: num_t<0> , num_t<13> , num_t<42> , etc. No more than for convenience, we endow this structure with a static numeric value , which will allow us to explicitly get back a number from the template argument (by accessing some_num_type::value ) without resorting to type inference.

Binary search tree


Recursive definition of a binary search tree is convenient for direct implementation in the form of a template. Simplified definition

  WOOD: NIL |  [TREE, DATA, TREE]

can be rephrased as “a tree is an empty set OR a set of three elements: a tree (the so-called left subtree), data, a tree (the so-called right subtree)”.

In addition, as already mentioned, a binary search tree requires specifying an order relation on the set of values ​​stored in the nodes of the tree (we must be able to somehow compare and order the nodes, that is, have the operation “less”). The canonical approach is to partition the node data into a key and a value (we compare the keys, simply store the values), but in our implementation, in order to simplify the structure without loss of generality, we will consider the node data as a single type, to specify the same order relation, we use a special type Comp ( comparator , let 's talk about it further).

 ///   struct NIL {}; ///  template<typename T, typename Left, typename Right, typename Comp> struct node { using type = T; // node value using LT = Left; // left subtree using RT = Right; // right subtree using comp = Comp; // types comparator }; /// :    ( ) template <typename T, typename Comp> using leaf = node<T,NIL,NIL,Comp>;

Despite the fact that the order relation is still defined on the set of types stored in nodes, it is convenient to attribute it to the tree itself and to store it as part of the type of this tree: when calling metafunctions for searching, inserting and traversing a non-empty tree, there is no need for additional indication of the comparator.

About fathers and children:
The attentive reader will notice that the presented structure lacks one element that is important for the implementation of most algorithms: references to the parent node (in our case, aliases of the type of the parent tree). Noticing this and trying to correct this injustice, the reader sooner or later in horror realizes that in this case there will be a cyclical dependence of pseudonyms .

The situation itself is not critical and has a workaround in the form of separating declarations and type definitions:
 template<...> struct one { struct two; using three = one<two, ...>; struct two : one<three, ...> {}; };
Note: it was experimentally found that such structures are compiled and instantiated by modern gcc and clang, however, I have not yet verified the strict adherence to the standard for declarations of such unusual patterns.
However, in practice it is very, VERY difficult to work with such entities and create them. The reciprocal reference to the parent element produces an interesting effect: in fact, our "simply connected tree" turns into a real graph (tasty!), Which, with any modification, must instantiate itself "at a time", again and completely (sadly). A deeper analysis of this situation is beyond the scope of this article and is among my future plans for exploring the possibilities of metaprogramming in C ++.

This is not the only way to implement and represent a tree (for example, you can store nodes in a tuple and index them), but this description is more intuitive and convenient for directly applying tree-working algorithms.

Order relationship


The Comp structure must contain type comparison metafunctions (i.e., less than and equal to operation patterns). Let us write an example of such a comparator based on the sizeof 'ah types (perhaps, the only numerical characteristic defined for all full types):

 struct sizeof_comp { template <typename U, typename V> struct lt : std::integral_constant<bool, (sizeof(U) < sizeof(V))> {}; //  template <typename U, typename V> struct eq : std::integral_constant<bool, (sizeof(U) == sizeof(V))> {}; //  };

Here everything should be transparent: lt is a “less” metafunction for types, eq is an “equal” metafunction. The approach shown earlier for determining the types of numbers was used: inheritance from std::integral_constant will endow the instantiated lt and eq static Boolean values.

In practice, concrete trees of specific types should be supplied with a comparator specific for this task. For example, we write a comparator for the class of “numeric types” described earlier:

 struct num_comp { template <typename U, typename V> struct lt : std::integral_constant<bool, (U::value < V::value)> {}; template <typename U, typename V> struct eq : std::integral_constant<bool, (U::value == V::value)> {}; };

Such a comparator, generally speaking, is universal and can compare any types containing a static value value .

About generating a comparator using CRTP:
Earlier in the theoretical section it was mentioned that the operation “less” is generally enough to intuitively determine the operation “equal”. We use an approach similar to CRTP ( Curiously recurring template pattern ) to determine the full comparator based only on the comparator containing the “less” operation (metafunction):
 ///        template <typename lt_traits> struct eq_comp { template <typename U, typename V> struct lt : std::integral_constant<bool, lt_traits::template lt<U,V>::value> {}; template <typename U, typename V> struct eq : std::integral_constant<bool, (!lt<U,V>::value && !lt<V,U>::value)> {}; }; ///   sizeof,     eq_comp::eq struct sizeof_comp : public eq_comp<sizeof_comp> { template <typename U, typename V> struct lt : std::integral_constant<bool, (sizeof(U) < sizeof(V))> {}; }; ///   num_t struct num_comp : public eq_comp<num_comp> { template <typename U, typename V> struct lt : std::integral_constant<bool, (U::value < V::value)> {}; };
The size of the definition has decreased and a mathematical background has appeared - isn't it beautiful?

Now we have everything to define the first type tree: “hands”;

 using t1 = node< num_t<5>, node< num_t<3>, leaf<num_t<2>>, leaf<num_t<4>> >, node< num_t<7>, NIL, leaf<num_t<8>> > >;
Note: Here and hereinafter in the examples, the default is to compare num_comp , explicitly indicating it in the list of template arguments is omitted. In general, after the development of the insert operation, we will not have to build trees in this way (by definition).
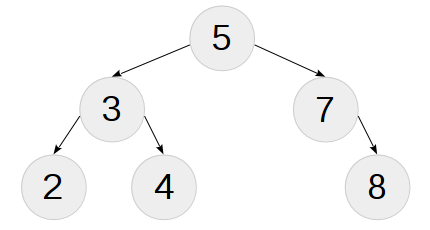
The described tree is shown in the picture.

About debugging at compile time:
How do we make sure that the class we define accurately describes what we have in mind?

This separate interesting topic for discussion and research is the debugging of metaprograms. We have no call stack, no variables, no fucking banal printf/std::cout . There are techniques that allow typing readable inferred types inside the compiler error messages, and, in principle, this is quite a useful feature for checking generated structures (for example, after modifying a tree).

We will not deal here with the issue of multi-megabyte error messages simply in the case of an incorrect program: after some practice this ceases to be a problem, since in the overwhelming majority of cases only the first instantiation error leads to a cascade of further errors: debugging in this case is carried out using the “successive approximation method”.

But, as paradoxical as it sounds, what to do if the program was compiled successfully? Here the author is more free to choose debugging methods. The type of the result of metafunctions, like those defined in type_traits can be simply printed as typeid(t).name() (starting from C ++ 11, you can legally look into RTTI). Simple data structures can be displayed on the screen with special metafunctions with tail recursion; for complex ones, printers will have to be built, comparable in complexity to operations on the structure itself.

The library of trees contains such a printer and examples of its use; the reader can get acquainted with them through the link to github at the end of the article. For example, the printed tree from the example above:
                   / - {2}  
          / - {3} - <
                   \--{four}  
 - {5} --- <
          \ - {7} - \
                   \--{eight}

Height


Let's look at the recursive function of calculating the height of a binary tree:

  /// Input: T - tree, exit: h - height 
 
  HEIGHT (T): 
      IF T == NIL 
          OUTPUT 0 
      ANYWAY 
          OUTPUT 1 + MAX (HEIGHT (T.LEFT), HEIGHT (T.RIGHT))

She is beautiful. Just take and transfer this function to C ++:

 ///    template <typename Tree> struct height; ///  : " T == NIL" template <> struct height<NIL> : std::integral_constant<size_t, 0> {}; ///    () template <typename Tree> struct height { static constexpr size_t value = 1 + max( height<typename Tree::LT>::value, height<typename Tree::RT>::value ); };
Note: we deliberately went for a small simplification, because of which the calculated tree height will be 1 more than its mathematical definition (the height of the empty set is not defined). , 1 , height .
: height , value = 0 , , ( NIL ), . C++: , ( ), ( Tree::LT , Tree NIL ).

max . constexpr ( , ), :

 template <typename T> constexpr T max(T a, T b) { return a < b ? b : a; }

, height :

 static_assert(height<t1>::value == 3, "");

«» height : n , n — ; h — .. .

?!
, , , : (!), - , . , : , constexpr - variadic- .

: , gcc-5.4 « » ( ) 900 . , ( ). , height gcc, > 900. O - ( ), .

, C++14 ( std::integer_sequence ): N 0..N-1, , . , , ( , 30- 9000- ).

, (.. ) : . ( , ..), , — , — API , , — ( « 24 »!).


( in-order traversal )


The task of traversing is to form a list of nodes in a certain way (or data from nodes, a question of terminology and matters in practice). A centered (symmetric) bypass is a bypass in which the root of the tree takes place between the results of the corresponding bypass of the left and right subtrees. Together with the property of a binary search tree (which is about inequalities, see theory), this suggests that a centered search of a binary search tree will form a sorted list of nodes for us - cool! Here's what a walk through a previously defined tree would look like:


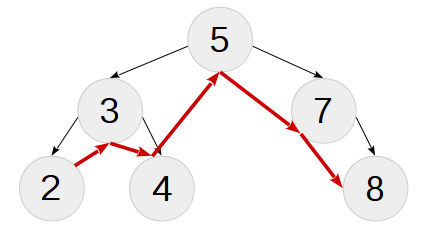
The recursive traversal algorithm is fairly simple:

 /// Input: T - tree, output: w - list of data from in-order bypass nodes 
 
INORDER (T):
    IF T == NIL
        CONCLUSION {}
    ANYWAY
         INORDER(T.LEFT) + {T.KEY} + INORDER(T.RIGHT)

"+" . -, , , — . — :

 ///    template <typename Tree> struct walk; ///  : " T == NIL" template <> struct walk<NIL> { using type = std::tuple<>; }; ///    () template <typename Tree> struct walk { private: //    using accL = typename walk<typename Tree::LT>::type; //   using accX = tuple_push_t<accL, typename Tree::type>; //      using accR = tuple_concat_t<accX, typename walk<typename Tree::RT>::type>; public: //  using type = accR; };

private : , , . , ?

walk : O(n) , n — ( O - : 3n ). , tuple_concat tuple_push 1 , ( parameter pack '). , height , h — .

:
: , , .

: , , , . , : « ». , : , .


Search


( ). , Comp . :

 /// : T - , k - -,
/// : N - ,   k` == k    
 
SEARCH(T,k):
     T == NIL  k == T.KEY
         T
    
         k < T.KEY
             SEARCH(T.LEFT, k)
        
             SEARCH(T.RIGHT, k)

:

 ///    template <typename Tree, typename T> struct search; ///     template <typename T> struct search<NIL,T> { using type = NIL; }; ///    template <typename Tree, typename T> struct search { using Comp = typename Tree::comp; using type = typename std::conditional< Comp::template eq<T, typename Tree::type>::value, // k == T.KEY ? Tree, //  , : typename std::conditional< Comp::template lt<T, typename Tree::type>::value, // k < T.KEY ? typename search<typename Tree::LT, T>::type, //     typename search<typename Tree::RT, T>::type //  --   >::type >::type; };

, : -, ( ), -, , , . :


search — - O(n) , — h ( ). «!» — , — « ?»

- std::conditional ?: : , (, , ). std::conditional ( ), std::conditional , .

— , . - «» , ( ), O(h) , , , .

( , . ):

 using found3 = search_t<NIL, num_t<0>, num_comp>; //    using found4 = search_t<t1, num_t<5>, num_comp>; //    using found5 = search_t<t1, num_t<8>, num_comp>; //    static_assert(std::is_same<found3, NIL>::value, ""); //   static_assert(std::is_same<found4, t1>::value, ""); //   static_assert(std::is_same<found5, leaf<num_t<8>>>::value, ""); //

This may seem strange: we are looking for a node in the tree with a type ... which is actually already specified as an argument - why? In fact, there is nothing unusual in this - we are looking for a type that is equal to the argument in terms of the comparator . The STL ( std::map) trees are also stored in the nodes of the pair ( std::pair), and the first element of the pair is considered the key , which, in fact, participates in comparisons. It is enough to keep the same in our tree std::pairand make the comparator Compcompare pairs of the first type in a pair - and get a classic associative (meta) container! We will return to this idea at the end of the article.

Insert


It is time to learn how to build trees with the help of metafunctions (it wasn’t all for the same thing to draw trees with your hands the way we did before?). Our recursive insertion algorithm will create a new tree:

 /// Input: T is a tree, k is a key type for insertion,
/// exit: T 'is a new tree with an inserted element 
 
INSERT (T, k):
    IF T == NIL
        CONCLUSION {NIL, k, NIL}
    ANYWAY
        IF k <T.KEY
            OUTPUT {INSERT (T.LEFT, k), T.KEY, T.RIGHT}
        ANYWAY
            CONCLUSION {T.LEFT, T.KEY, INSERT (T.RIGHT, k)}

Let us explain its work: if the tree into which the insertion occurs is empty, then the inserted element will create a new tree {NIL, k, NIL} , i.e. just a sheet with this element (bottom of recursion). If the tree is not empty, then we must recursively fall to an empty tree (i.e., until the left or right subtrees are empty), and eventually form the same sheet {NIL, k, NIL} in this subtree instead NIL , on the way “hanging up” itself in the form of a new left or right subtree. In the world of types, we cannot change existing types, but we can create new ones - this happens at every step of recursion. Implementation:

 template <typename Tree, typename T, typename Comp = typename Tree::comp> struct insert; ///   template <typename T, typename Comp> struct insert<NIL,T,Comp> { using type = leaf<T,Comp>; }; ///   template <typename Tree, typename T, typename Comp> struct insert { using type = typename std::conditional< Comp::template lt<T, typename Tree::type>::value, // k < T.KEY? node<typename Tree::type, //   {INSERT(T.LEFT,k), T.KEY, T.RIGHT} typename insert<typename Tree::LT, T, Comp>::type, typename Tree::RT, Comp>, node<typename Tree::type, //   {T.LEFT, T.KEY, INSERT(T.RIGHT,k)} typename Tree::LT, typename insert<typename Tree::RT, T, Comp>::type, Comp> >::type; };

Comp ; , - * .

: O(n) (n — ), h (h — ). :

 using t2 = leaf<num_t<5>, num_comp>; using t3 = insert_t<t2, num_t<3>>; using t4 = insert_t<t3, num_t<7>>; static_assert(height<t4>::value == 2, ""); //  2  using t5 = insert_t<insert_t<insert_t<t4, num_t<2>>, num_t<4>>, num_t<8>>; static_assert(std::is_same<t5, t1>::value, ""); //

insert_tuple , ( insert ), :

 using t6 = insert_tuple_t<NIL, std::tuple< num_t<5>, num_t<7>, num_t<3>, num_t<4>, num_t<2>, num_t<8> >, num_comp>; static_assert(std::is_same<t1, t6>::value, "");

( breadth-first traversal )


Traversing the width of a binary tree (or a search for width from graph theory) generates a list of nodes in order “by level” —first it outputs the root, then the nodes with a depth of 1, then with a depth of 2, etc. The algorithm for this traversal uses a queue of nodes for further output (and not a stack ), so it is difficult to "convert" into recursive. Under the spoiler further interested reader will find a workaround. Here we note only the useful fact that a tree “parsed” by a wide walk can be assembled back into exactly the same successive insertion of elements from the tuple of the walk result. The figure shows a walk around the width of our test tree:


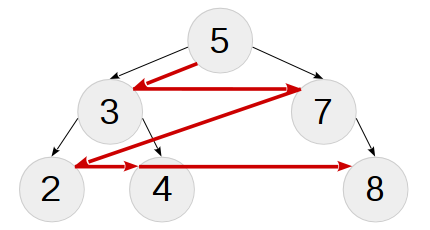
Recursive wide bypass:
: 0 h . :

 /// : T - , l -   ,
/// : t -     
COLLECT_LEVEL(T,l):
     T == NIL
         {}
    
         l == 0
             {T.KEY}
        
             COLLECT_LEVEL(T.LEFT,l-1) + COLLECT_LEVEL(T.RIGHT,l-1)

. , O(nh) - (, , collect_level ).


Delete?


Deleting a node is not a trivial task. The classical approach considers 3 cases (by the number of child nodes), and the algorithm uses the concepts of the subsequent and the parent node. Without a reverse link to the parent node (see the “About Fathers and Children” spoiler), it is problematic to implement the algorithm effectively: each lifting operation up the tree will have to have O (n) complexity . A naive implementation of such a deletion will lead to a “combinatorial explosion” in the number of instantiations (the complexity is something around O (n n ) ). The development of the node deletion metafunction is included in future plans to improve the library. See UPD2 at the end of the article.

Application


Let's take a breath and finally pay attention to the question, why might a binary search tree need compile time ? There are three answers:

Nonconstructive:
* Picture with trolleybus *. Omit.

Evident:
... for those with a research interest

Constructive:
Let us give examples of possible applications of such a structure:


:
«Modern C++ Design: Generic Programming and Design Patterns Applied» ( « ++» , . ) : « ». static_assert , C++11, ( , policy ), STL, C++98 (« ») ( , , , ).

, : compile-time — , ( , ), ( «», , - ).

, . ( ), , .. , « » . , — ( ) compile-time ( ), , , .

What then?


: ...
, (, , ) . — , (, - ), std - ( — tutorial ). , .

!

Literature



→ UPD repository

:
Rehab std :: conditional:
izvolov std::conditional . search O(h) :
 template <typename Node, typename T, typename Comp> struct search { using type = typename std::conditional< Comp::template eq<T, typename Node::type>::value, Node, typename search<typename std::conditional< Comp::template lt<T, typename Node::type>::value, typename Node::LT, typename Node::RT >::type, T, Comp>::type >::type; };
(+ insert ) .


UPD2:
The implementation of remove and fix insert and search for O (h):
, insert search remove O(h) ( insert ). SFINAE + decltype ( , . ). remove :
 template <typename Tree, typename T> struct remove { private: enum : bool { is_less = Tree::comp::template lt<T, typename Tree::type>::value }; enum : bool { is_equal = Tree::comp::template eq<T, typename Tree::type>::value }; enum : size_t { children = children_amount<Tree>::value }; using key = typename min_node_t< typename std::conditional< is_equal && children == 2, typename Tree::RT, leaf<typename Tree::type, typename Tree::comp> >::type >::type; using recursive_call = typename remove< typename std::conditional< is_less, typename Tree::LT, typename std::conditional< !is_equal || children == 2, typename Tree::RT, NIL >::type >::type, typename std::conditional< is_equal, key, T >::type >::type; static typename Tree::RT root_dispatcher(...); template <typename Bush> static typename std::enable_if< sizeof(typename Bush::LT::type), typename Bush::LT >::type root_dispatcher(Bush&&); public: using type = typename std::conditional< is_equal && (children < 2), decltype(root_dispatcher(std::declval<Tree>())), node< key, typename std::conditional< is_less, recursive_call, typename Tree::LT >::type, typename std::conditional< !is_less, recursive_call, typename Tree::RT >::type, typename Tree::comp > >::type; };
, , . , , , , .

Source: https://habr.com/ru/post/320686/

More articles:


All Articles