Simple Wolfram Language http server

Preamble

Schematic diagram of the server

The idea of ​​writing this article came to me after reading a similar article on Habrahabr, which tells how to create your own localhost server using Mathematica. The web server itself was written using Python and the extensible Tornado server. He processed requests and sent responses in json format, and the logic was implemented in Mathematica. At the same time, communication between Python and Mathematica occurred via the command line, and each request to the server restarted the Mathematics core. The remaining details can be found in the article itself by the author @Nilis . Here I would like to show you how to write simple code that will perform similar functions — that is, create an http server to process requests and send responses. Plus I would like to show some interesting features of Wolfram Language and its syntax.

Empty server implementation

The easiest way is to start the implementation with the main function, and then move deeper. In order to write it, you need to load the SocketLink context by executing the following command:

Needs["SocketLink`"]; 

After that, the functions of this context become available. You can see which functions it contains in the following way:

 Information["SocketLink`*"]; 

Let us explain what each of them represents:

1. CreateClientSocket [ port ] - creates a socket using the port - port ;
2. CreateServerSocket [ host , port ] - creates a client socket connecting to the host - host and using the port - port ;
3. OpenSocketStreams [ socket ] - opens a stream of input and output on the socket - socket ;
4. CreateAsynchronousServer [ socket , handler ] - creates a "server" with the specified socket - socket and handler - handler .

In the simplest case, we need only two functions from this context:

CreateAsynchronousServer and CreateServerSocket . Of course at first glance it seems that everything is already ready and there is no point in " writing " the server. But it is not. CreateAsynchronousServer - can not do anything except listen to the specified socket. So we have to implement everything else. To begin with, it would be nice to create an auxiliary function that will have a restriction on the input arguments:

 MathematicaSimpleServer[socket_Socket, handler_Handler] := CreateAsynchronousServer[socket, handler]; 

Explanation for non Mathematica users. To the left of the " : = " sign ( SetDelayed [] ) there is a template, which after execution will be stored in memory. On the right is the rule that will be executed when the pattern is encountered. Note socket_Socket indicates that the first argument must be a socket. Template handler_Handler - says that the second argument must be of type Handler . This type does not currently exist. However, Mathematica does not pay attention to this and allows in any case to create a function that will take a non-existent type as one of the input parameters.

If this type does not exist, then it must be created. Let's do it. The following code shows how Mathematica can create its own simple data type using TagSetDelayed [] :

 (* getters for Handler *) Handler /: GetRequestParser[Handler[parser_RequestParser, _]] := parser; Handler /: GetResponseGenerator[Handler[_, generator_ResponseGenerator]] := generator; (* setters for Handler *) Handler /: SetRequestParser[handler_Handler, parser_RequestParser] := Handler[handler, GetResponseGenerator[handler]]; Handler /: SetResponseGenerator[handler_Handler, generator_ResponseGenerator] := Handler[GetRequestParser[handler], generator]; 

Explanation of syntax for non-Mathematica users. The symbol " /: " ( TagSetDelayed [] ) means that only for the data type ( Handler ), which is on the left, the operation of the function, whose definition is entirely on the right, will be redefined. The rule that will be executed when the function is called is normally to the right of the " : = " sign. This method will also work for protected system functions. Since in this case there is a change associated not with the name of the function itself, but with the name of the type. Some peculiarity lies in the fact that inside the template between the characters " /: " and " : = " must be in an explicit form somewhere there is a type Handler (but not at the top level). Again, it is worth noting that the four functions above have been defined using yet non-existing data types: RequestParser , ResponseGenerator . Now the final touch in the handler definition is to create a template that will be executed when the handler is called inside the server. He is obliged to accept as input a list of two elements — input and output streams. Actions with these streams can be performed almost any. As mentioned above, the handler must read the input stream and write to the output stream. We implement it as follows:

 handler_Handler[{input_InputStream, output_OutputStream}] := Module[{ requestParser = GetRequestParser[handler], responseGenerator = GetResponseGenerator[handler], request = "", response = "" }, (* read data from input stream of the socket *) {request} = If[# != {}, FromCharacterCode[#], Print[DateString[], "\nERROR"]; Close[input]; Close[output]; Return[]]& @ Last[Reap[While[True, TimeConstrained[ Sow[BinaryRead[input]], 0.01, (Close[input]; Break[]) ];];]]; (* logging *) Print[DateString[], "\nREQUEST:\n\n", request]; (* processing request *) response = responseGenerator[requestParser[request]]; (* logging and writing data to the output stream *) Switch[response, _String, Print[DateString[], "\nRESPONSE:\n\n", response]; BinaryWrite[output, ToCharacterCode[response]], {__Integer}, Print[DateString[], "\nRESPONSE:\n\n", FromCharacterCode[response]]; BinaryWrite[output, response]; ]; Close[output]; ]; 

Oddly enough - but for Mathematica it is not necessary to create any one unique name on the left side of the template. This can be a complex expression with a header and internal content. This way of creating function definitions is rarely used, but in our case it will be very useful. The internal contents of the handler determine the entire server operation logic. Now the empty server implementation is ready. It will be working, but it will not do anything useful. After all, all the processing of the request lies on non-existent functions: requestParser , responseGenerator . In our case, a string is passed to their input, and the result must also be a string (or a list of bytes, which is hinted at by the second choice in the Swich [] switch). Although no one bothers to return anything after a request, only on the condition that this “ anything ” will be correctly processed by the function for creating answers.

Processing request

Now that the server is ready, you need to take care of the implementation of the RequestParser type. It will be used first. In the same way as was done above for Handler , we will create the simplest definition:

 requestParser_RequestParser[request_String] := request; 

According to this definition, the function will simply return the query string itself. To begin with, that's enough. Now everything is the same, but for the answer generator:

 responseGenerator_ResponseGenerator[parsed_String] := "HTTP/1.1 200 OK Content-Length: 1024 Connection: close <!DOCTYPE html> <html> <head> <meta http-equiv=\"Content-Type\" content=\"text/html; charset=utf-8\" /> <title>MathematicaSimpleServer</title> </head> <body> Hello from mathematica simple server! </body> </html>" 

The definition of the generator is the simplest. This is just the answer line connected to the html markup of the displayed page. Now everything is ready! You can try to start the server and check how it will work. You can do this by running the following code:

 socket = CreateServerSocket[8888]; handler = Handler[RequestParser[], ResponseGenerator[]]; server = MathematicaSimpleServer[socket, handler]; 

Now open the browser and go to http: // localhost: 8888 / . The following page will be displayed in the browser:

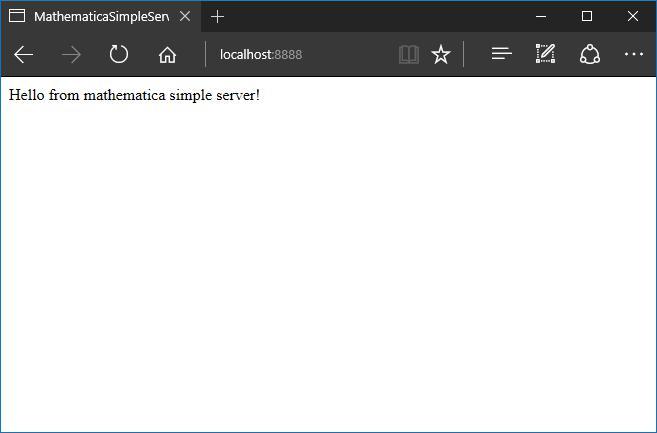
 Thu 19 Jan 2017 01:22:00 REQUEST: GET / HTTP/1.1 Accept: text/html, application/xhtml+xml, image/jxr, */* Accept-Language: ru-RU User-Agent: Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/51.0.2704.79 Safari/537.36 Edge/14.14393 Accept-Encoding: gzip, deflate Host: localhost:8888 Connection: Keep-Alive 

 Wed 18 Jan 2017 14:56:45 RESPONSE: HTTP/1.1 200 OK Content-Length: 1024 Connection: close <!DOCTYPE html> <html> <head> <meta http-equiv="Content-Type" content="text/html; charset=utf-8" /> <title>MathematicaSimpleServer</title> </head> <body> Hello from mathematica simple server! </body> </html> 

Hooray! Our server still works. I wonder what will happen if we do not stop it and try to change the code of the displayed html page, which is returned during the call to ResponseGenerator [] ? Let's do it - just define the function again:

 responseGenerator_ResponseGenerator[parsed_String] := ("HTTP/1.1 200 OK Content-Type: text/html; charset=utf-8 Content-Length: " <> ToString[StringLength[#]] <> " Connection: close " <> #)& @ "<!DOCTYPE html> <html> <head> <meta http-equiv=\"Content-Type\" content=\"text/html; charset=utf-8\" /> <title>MathematicaSimpleServer</title> </head> <body> Hello from mathematica simple server! <br/> we changed the server logic without stopping ;) </body> </html>" 

After executing the code above and refreshing the page, the modified content is displayed in the browser. It turns out that you can not stop the web server and continue to add new definitions for the ResponseGenerator and RequestParser . Nevertheless, it is useful to know how to stop it. It is enough to execute the code:

 SocketLink`Sockets`CloseSocket[socket]; StopAsynchronousTask[server]; 

Server Expansion

A little preparation. To avoid any further problems, we will immediately set up as the working directory for the location of this document:

 SetDirectory[NotebookDirectory[]]; 

Obviously, displaying two lines in a browser window is not a good demonstration of Mathematica's capabilities. For the sake of test purposes, we will create a simple html index page. The page code is shown below. There are already several links to other addresses that the server should return. Also added a function that creates the answer itself entirely.

 IndexPage[] := "<!DOCTYPE html> <html> <head> <meta http-equiv=\"Content-Type\" content=\"text/html; charset=utf-8\" /> <title>MathematicaSimpleServer</title> <link rel=\"icon\" type=\"image/png\" href=\"/favicon.png\"/> </head> <body> Index page for the mathematica simple server <ul> <li><a href=\"/graphic?Sin\" >graphic</a></li> <li><a href=\"/page.html\" >page</a></li> <li><a href=\"notebook.nb\" >notebook</a></li> </ul> </body> </html>"; ResponseString[page_String] := StringTemplate["HTTP/1.1 200 OK Content-Type: text/html; charset=utf-8 Content-Length: `length` Connection: close `page`"][<|"length" -> StringLength[page], "page" -> page|>]; ResponseString[page_String, length_Integer] := StringTemplate["HTTP/1.1 200 OK Content-Type: text/html; charset=utf-8 Content-Length: `length` Connection: close `page`"][<|"length" -> length, "page" -> page|>]; 

The function that connects the response string and the page markup code - ResponseString [] - has two definitions: the first one calculates the page size and replaces the value of the Content-Length header with the result. In the second definition, you can specify the size of the response body. As mentioned above, there are several links on the main page. It is assumed that the links lead to one of the addresses where some server logic is executed. A total of four different cases are the display of the main page itself, a link to an arbitrary graph, to the html page and to the page formed from the finished Mathematics notebook. Each of the cases must be considered separately. The first case, loading the main page. It is executed only if a GET request has been received at the address "/" or "/ index". How to check this address? You can do it in various ways. The following is not the most popular, but interesting. First, override the Keys and Part functions on the RequestParser data type as follows:

 RequestParser /: Keys[RequestParser[rules___Rule]] := {rules}[[All, 1]]; RequestParser /: Part[RequestParser[___, "Address" -> function: (_Symbol|_Function), ___], "Address"] := function; 

It is worth explaining the syntax of the expressions above. rules___Rule - is a template with an arbitrary (including zero) number of replacement rules. This means that RequestParser can be created using any number of processing functions, and all the names of these functions can be obtained simply by using the Keys function. Interestingly, Keys is a system function with a Protected attribute, which prohibits changing this function, but specifying a type using TagSetDelayed allows it. Similarly, the built-in Part function was overridden. As mentioned above, it is assumed that RequestParser is a complex expression that must contain a set of rules within itself. Each rule is a key and a value (a function to process). Why is all this needed? Writing a large number of conditions and checking the query string is hard enough. It is all the more easy to make a mistake in the order of definitions, since if it is bad to choose a regular expression or pattern for checking the request, then some sections of the code will be unattainable. It is much easier to process a single request with several functions at once and return the result as an association with pairs: the name of the function and the result. Below is the implementation of this method:

 requestParser_RequestParser[request_String] /; MatchQ[requestParser, RequestParser[_String -> (_Symbol|_Function)]] := Association[Map[Function[key, key -> (requestParser[[key]])[request]], Keys[requestParser]]]; 

Now you need to create those same functions. We will have only one such function to get the address from the request method, because the author’s fantasy has managed to fit all the variability of the server’s work only into the difference of addresses in the first query line.

 TakeAddress[request_String] := First[StringCases["GET " ~~ address___ ~~ " HTTP/" -> address][request]]; 

For those who are not familiar with Mathematica, there are many interesting constructs for string expressions in the language. The construction above is intuitive, it simply selects all the text that is between GET and HTTP in the first line. In a previous server implementation, the response generator processed the string that the request handler returned. But now the input from the key-value pairs will be passed to the input of this function. So it is necessary for the generator to create a new definition that can convert the resulting association into an answer.

 responseGenerator_ResponseGenerator[parsed_Association] /; parsed[["Address"]] == "/" || parsed[["Address"]] == "/index" := ResponseString[IndexPage[]]; 

Restart the server with a new handler. Now inside RequestParser there is an explicit indication of the name of the function - "Address" - and the function itself - TakeAddress - with which all answers are processed.

 socket = CreateServerSocket[8888]; handler = Handler[RequestParser["Address" -> TakeAddress], ResponseGenerator[]]; server = MathematicaSimpleServer[socket, handler]; 

Home page is working. Add the correct processing of requests to other resources. The first of these is an attempt to obtain a graph of the specified function. First we add the definition to the response generator. Another great feature of Mathematica. You can redefine a function not only by specifying other types of arguments or another number of them. You can also set an arbitrary complex condition for executing a function using the " /; " ( Condition [] ) sign. The condition is most conveniently written between the template itself (name and function arguments / signature) after the " /; " sign and before the " : = " sign.

 responseGenerator_ResponseGenerator[parsed_Association] /; StringMatchQ[parsed[["Address"]], "/graphic?" ~~ ___] := Module[{function = ToExpression[StringSplit[parsed[["Address"]], "?"][[-1]]]}, ResponseString[ExportString[Plot[function[x], {x, -5, 5}], "SVG"]] ]; 

You can check how it will work - go to the first link on the page http: // localhost: 8888 / index or simply at http: // localhost: 8888 / graphic? Sin . Now it shows the following:

If instead of ../graphic?Sin you write ../graphic?Cos or even Log / Exp / Sqrt / Function [x, x ^ 3] / t.d., the corresponding graph will be displayed on the page. Now let's add to the handler the ability to display an arbitrary html page that is located in the working directory or in one of the subdirectories. To begin, create this page using the code:

 Export["page.html", TableForm[Table[{ToString[i] <> "!", i!}, {i, 1, 9}]], "HTML"]; 

Unfortunately, anyone who executes the code from the line above will immediately notice that exporting Mathematica expressions to html takes a lot of time. It turns out that for Mathematics it will not be difficult to create many pages or other elements (pictures / tables), but the export of all this data will take much more time each time than the creation by standard means. Well. We will assume that all pages already exist and are located on the disk in the working directory of the server - where we just saved the test page. Now let's try to display it. In this case, the page and any of its elements are imported as a list of bytes and are connected to the list of bytes that correspond to the line with the response headers.

 responseGenerator_ResponseGenerator[parsed_Association] /; FileExistsQ[FileNameJoin[{Directory[], parsed[["Address"]]}]] && StringTake[parsed[["Address"]], -3] != ".nb" := Module[{path = FileNameJoin[{Directory[], parsed[["Address"]]}], data}, data = Import[path, "Byte"]; Join[ToCharacterCode[ResponseString["", Length[data]]], data] ];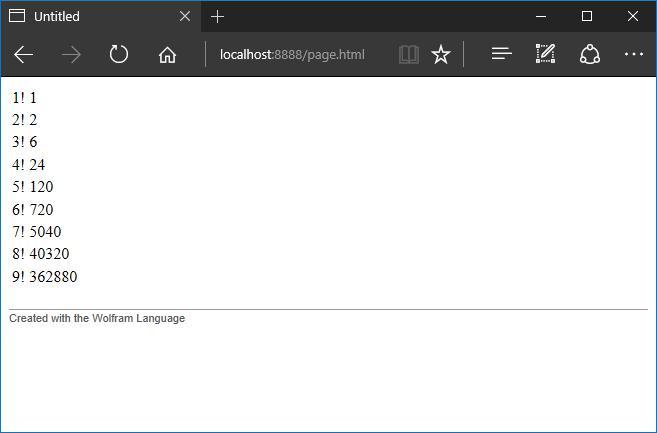 

As expected, the server returned a table of factorial integers to the browser. The last case. Display in your browser a saved notepad. In the working directory, create a new notebook notebook.nb with the code:

 notebook = CreateDocument[{TextCell["Bubble sort","Section"], ExpressionCell[Defer[list = RandomInteger[{0, 9}, 20]], "Input"], ExpressionCell[Defer[list //. {firsts___, prev_, next_, lasts___} :> {firsts, next, prev, lasts} /; next < prev], "Input"] }]; NotebookEvaluate[notebook, InsertResults -> True]; NotebookSave[notebook, FileNameJoin[{Directory[], "notebook.nb"}]] NotebookClose[notebook]; 

Now we perform actions similar to those that occurred when html-page was requested. But before returning the html code, the notepad is first converted to html.

 responseGenerator_ResponseGenerator[parsed_Association] /; FileExistsQ[FileNameJoin[{Directory[], parsed[["Address"]]}]] && StringTake[parsed[["Address"]], -3] == ".nb" := Module[{path, data, notebook}, path = FileNameJoin[{Directory[], parsed[["Address"]]}]; notebook = Import[path, "NB"]; Export[path <> ".html", notebook, "HTML"]; data = Import[path <> ".html", "Byte"]; Join[ToCharacterCode[ResponseString["", Length[data]]], data] ]; 

The exact display of the notebook in the browser of course will not. It all depends on the way Math exports the notepad to html. Also for our server, it would be worthwhile to add an error page that will be displayed to the user in the absence of a resource.

 responseGenerator_ResponseGenerator[parsed_Association] /; !FileExistsQ[FileNameJoin[{Directory[], parsed[["Address"]]}]] := Join[ToCharacterCode[StringReplace[ResponseString["Page not found"], "200 OK" -> "404 !OK"]]]; 

Obviously, the web server implementation shown in this article is not even close. Moreover, it has major drawbacks. As an example, you can give at least the fact that the server is able to return only two codes: 200 and 404. Therefore, the presented code is best viewed as experimental / demonstrative.

Legal aspect

As it became known to the author, the standard license for Wolfram Mathematica does not allow the use of the Mathematics core inside server applications for both commercial and personal purposes. This restriction does not apply to scheduled tasks that should not be associated with the web. Wolfram Research has its own very good platform for implementing large (and not so) server applications - this is webMathematica. It is the license for webMathematica that makes it possible to avoid problems with the law and use Wolfram Language on the server, and it does not matter if the application is developed on it (webMathematica) or not, you still have to purchase a license. The author is of the opinion that his code does not violate any license agreements, because here it shows just the text of the program that allows the Mathematica built-in tools to run a web server on localhost. After all, a detective story in which a crime is described is not in itself a crime.

Conclusion

In this article I wanted to demonstrate first of all the interesting syntactic features of Wolfram Language. Various ways of creating functions, rules and conditions when solving a specific task in a non-standard way. I also hope that this guide will allow enthusiasts to practice web development by combining this with learning Mathematica and its capabilities. In turn, I expect all sorts of tips to improve the code, possible ideas for the implementation of this task, as well as criticism and comments. Download the notebook containing this work at the following link . Thank you all for your attention!