Bitcoin in a nutshell - Blockchain
Blockchain is the technology on which Bitcoin is built. And if a couple of years ago, all the fame came to cryptocurrency, then today you can hear more and more bold phrases like: "Forget Bitcoin, Long Live Blockchain". Platforms like Ethereum, IPFS or Overstock are actively developing. They consider the blockchain not as a tool to create another payment system, but as a completely separate technology, comparable in its innovativeness to the Internet.
In this chapter, I will tell you what the Bitcoin blockchain is. Even compared to Ethereum, this is a terrible anachronism, but an understanding of the principles of its work will help you greatly if you decide to deal with more complex projects.

Book
- Bitcoin in a nutshell - Cryptography
- Bitcoin in a nutshell - Transaction
- Bitcoin in a nutshell - Protocol
- Bitcoin in a nutshell - Blockchain
- Bitcoin in a nutshell - Mining
Table of content
- Blockchain for dummies
- Structure
- Merkle tree
- Timestamp
- Raw block
- Links
Blockchain for dummies
The blockchain itself is an extremely simple thing. It is easiest to illustrate using the example of an accounting book in which all transactions in the Bitcoin network are recorded. Moreover, such a book is present for each member of the network, which means that anyone, if desired, can check whether this or that transaction was real or not.
And if the whole blockchain is a book, then individual blocks can be represented as pages on which transactions are recorded. Each block "refers" to the previous one and so on until the very first block ( genesis block ). This is what creates such an interesting feature of the blockchain as immutability. It is impossible to take and change the block # 123 so that no one noticed. Because the blockchain is designed in such a way that it will change the block # 124, then # 125 and so on, to the very top.
Structure
With a familiar hand movement we open the protocol specification and look at the block structure.
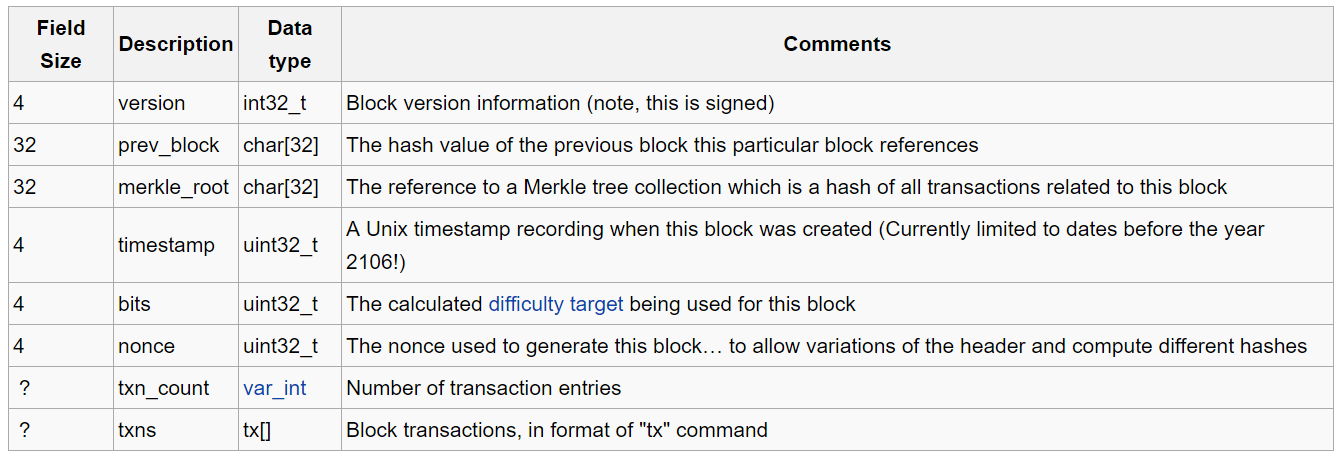
- version - block version
- prev_block - parent block hash
- merkle_root - if simplified, then this is a hash of all transactions in the block
- timestamp - date and time of block creation
- bits , nonce - I will tell you about these parameters in detail in the chapter Bitcoin in a nutshell - Mining
- txn_count , txns - the number of transactions in the block and their list
The first six parameters (all but txn_count and txns ) form the header of the block ( header ). It is the hash of the header that is called the block hash, that is, the transactions themselves are not directly involved in hashing.
Instead, they are entered into a special structure - the Merkle tree , which I will discuss below.
Merkle tree
Technical side
A merkle tree is a data structure, also known as a binary hash tree. In the case of Bitcoin, it is structured as follows:
First, the hashes of all transactions in the
hash_A = SHA256(SHA256(A))block arehash_A = SHA256(SHA256(A))Then the hashes of the transaction hashes amount
hash_AB = SHA256(SHA256(hash_A + hash_B))Similarly, we consider hashes of the sum of the resulting hashes
hash_ABCD = SHA256(SHA256(hash_AB + hash_CD))and further along the recursion. Lyrical digression - since the tree is binary, then at each step there must be an even number of elements. Therefore, if, for example, we have only three transactions, then the last transaction is simply duplicated:
- The process continues until a single hash is obtained - it is called merkle_root (the third field in the header of the block)
Below is the implementation of the Merkle tree, you can check it on any block.
import hashlib # Hash pairs of items recursively until a single value is obtained def merkle(hashList): if len(hashList) == 1: return hashList[0] newHashList = [] # Process pairs. For odd length, the last is skipped for i in range(0, len(hashList)-1, 2): newHashList.append(hash2(hashList[i], hashList[i+1])) if len(hashList) % 2 == 1: # odd, hash last item twice newHashList.append(hash2(hashList[-1], hashList[-1])) return merkle(newHashList) def hash2(a, b): # Reverse inputs before and after hashing # due to big-endian / little-endian nonsense a1 = a.decode('hex')[::-1] b1 = b.decode('hex')[::-1] h = hashlib.sha256(hashlib.sha256(a1 + b1).digest()).digest() return h[::-1].encode('hex') Immutability

Now about why this is needed in Bitcoin. I think you understand that if you change at least one transaction, then merkle_root will also change. Therefore, such a data structure allows to ensure that transactions are not "workable" in a block. That is, the following situation cannot happen:
Some of the miners found a new unit and began to scatter it over the network. At this time, the attacker intercepts the block and, for example, deletes any transaction from the block, after which it distributes the already changed block.
For verification, it is enough to count the merkle_root yourself and compare it with what is written in the header of the block.
SPV
But here it is reasonable to argue that, first, such difficulties are completely useless. It is enough just to count the hash of the sum of all transactions in the txns_hash = SHA256(SHA256(sum(txns))) — it will also change after any manipulations with transactions. And, secondly, what prevents the attacker to replace the merkle_root in the block? I will answer the second question right away: in fact, nothing can be changed in the block at all, because the block will immediately become invalid (you will understand this after reading the next chapter of Bitcoin in a nutshell - Mining ).
And the Merkle tree is actually needed in order to be able to create SPV nodes (Simplified Payment Verification). Such nodes synchronize only block headers, without the transactions themselves. As a result, the blockchain takes up less space (for beauty we take the height of 500.000 blocks, the size of the header is fixed - 80 bytes):
500.000 * 80/1024/1024 ≈ 40 MB
Such a blockchain can already easily fit on a phone, tablet or some IoT. What in the future should give greater decentralization, network security and so on.
The essence of simplified payment verification is as follows: let you have an SPV node. I have the entire blockchain entirely and I need to convince you that some transaction really was (in the picture this is transaction K ). In this case, I just need to provide you with a few hashes: H_L, H_IJ, H_MNOP, H_ABCDEFGH , they are also called the authentication path .
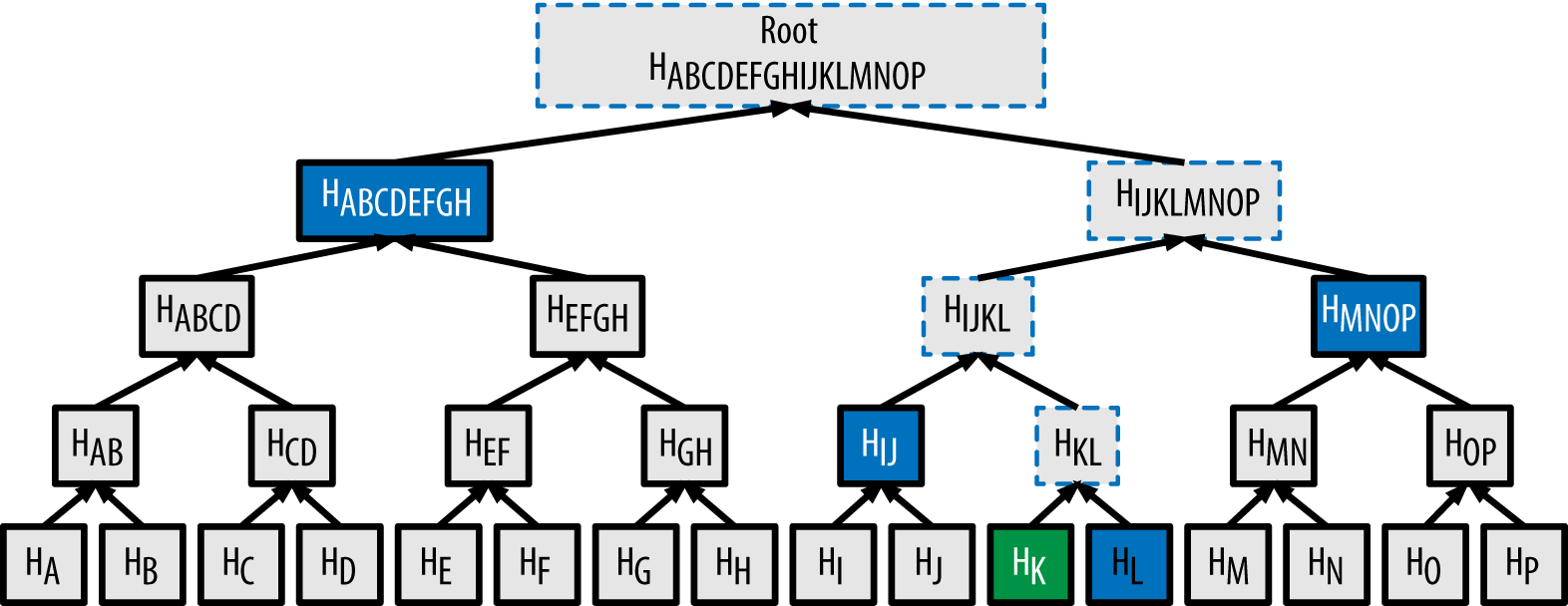
After that, you first consider H_K = SHA256(SHA256(K)) , then H_KL = SHA256(SHA256(H_K + H_L)) and so on to the very top. If in the end you find a block with the same merkle_root , then the fact of the existence of a transaction is considered confirmed.
BTW Ralph Merkle even patented his data structure, as evidenced by patent US4309569 A.
Timestamp
Another interesting question. Imagine that a new block appeared somewhere on the network and the nodes start transmitting it to each other. Each node should make sure that the block is correct. For this, she:
- checks syntax and block structure
- checks each transaction in a block for validity
- hashes transactions and compares merkle root
- checks several criteria related to mining, and so on
But how can I check the timestamp? It is clear that the time on different computers may vary, so even if the new block has a timestamp different from your current time an hour ahead, this does not mean that the block is "wrong", maybe the miner simply hastens the clock.
Therefore, to test the timestamp for validity, two criteria were invented. First, it must be greater than the arithmetic average timestamps of the previous 11 blocks. This is done so that it does not happen that block # 123 was released on March 12, 2011, and # 124 - on February 13, 1984. But at the same time, some error is allowed.
Secondly, the timestamp must be less than the network adjusted time . That is, the node, when receiving a new block, is interested in the current time from its "neighbors" on the network, considers the arithmetic average and if the block timestamp is less than the resulting value + 2 hours, then everything is fine.
BTW, as you can see, the timestamp of a new block may turn out to be even smaller than the timestamp of an earlier block. This is not such a rarity, for example # 145045 , # 145046 and # 145047 .
145044: 2011-09-12 15:46:39 145045: 2011-09-12 16:05:07 145046: 2011-09-12 16:00:05 // ~5 minutes before prior block 145047: 2011-09-12 15:53:36 // ~7 & ~12 minutes before 2 prior blocks 145048: 2011-09-12 16:04:06 // after 2 prior blocks but still before 145045 Raw block
If you still have any questions about the structure of the block, then I suggest you look at them in a "raw" form. The most obvious way to do this is to run bitcoind --daemon for a couple of hours, and then examine the already downloaded blocks. But, first of all, not everyone has the time / desire to synchronize the blockchain. Secondly, in Bitcoin blocks are stored in a very specific LevelDB database, also in a rather strange way . And since the book is designed not only for experienced developers, I will go through the proven way and use the protocol again in its original form.
To get the block, send the getdata message, in which we specify the type : MSG_BLOCK and hash : 000000000003ba27aa200b1cecaad478d2b00432346c3f1f3986da1afd33e506 is the hash of the block # 100.000 . The entire code can be viewed here .
def getdataMessage(): block_hash = '000000000003ba27aa200b1cecaad478d2b00432346c3f1f3986da1afd33e506' count = struct.pack("<B", 1) inventory = struct.pack("<L", 2) # type : MSG_BLOCK inventory += block_hash.decode('hex')[::-1] return count + inventory 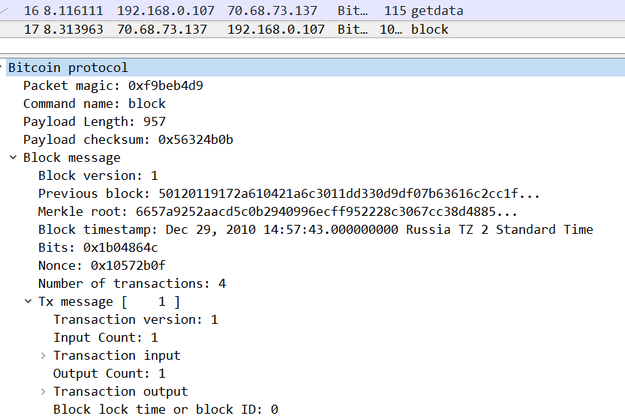
Links
')
Source: https://habr.com/ru/post/320176/
All Articles