Finite Difference Programming

Manually writing down the SLAE coefficients and entering them into the program is not the most effective way of programming the finite difference method, because for each new variation of the problem statement, it will be necessary to write a new program. It is more logical to develop a common solver for a wider class of tasks, which will simplify programming and testing. Testing of CDM algorithms is difficult, since the exact solution is unknown, but a common solver can be tested on problems with a given exact solution.

The author developed the Joker FDM solver for solving 1- and 2-dimensional conjugation problems for elliptic equations by the finite-difference method.

Formulation of the problem

Considered a rectangular area. The horizontal side of the rectangle is divided into 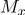intervals, vertical - on gaps. Thus, the entire rectangle is divided into rectangular subregions.

In each 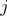th subdomain 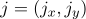, sets the system of differential equations of reaction-diffusion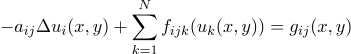

with the Dirichlet, Neumann, or Robin boundary conditions and the conjugation conditions of the type of non-ideal contact or ideal contact.

For a detailed task, see the GitHub Wiki , to view the formulas, install the extension for Chrome .

Solver was used by the author to calculate the solution to the diffusion model of complex heat exchange (a nonlinear system of two equations).

Not all finite element solvers have a function for solving pairing problems with a solution jump at the interface (non-ideal contact). Note the FEniCS package in which there is such a function.

Algorithm Description

A grid is entered in the region: each x- and y-gap is divided into equal parts.

A second-order difference scheme is used, described in the book “Difference Methods for Elliptic Equations” by Samarasky, Andreev.

For linearization of nonlinear equations, the Newton method is used. This method has proven itself to solve the equations of complex heat transfer.

The formulation and justification of the one-dimensional difference scheme, see the wiki .

Description of solver

1-dimensional solver is implemented on Octave and C ++, 2-dimensional - only on C ++.

Difference equations are written as a sum of one-dimensional difference operators in x and y and a nonlinear point operator. The implementation of the general algorithm through one-dimensional operators allows us not to consider a large number of node types (internal, on the side of the rectangle, at the corner point, at the interface of subregions, on the side of the rectangle and at the interface, at the corner point at the interfaces). To write equations using clear syntax with overloading operations.

To solve the SLAE, an iterative method from the MTL4 library is used .

In the future we plan to implement a 3-dimensional solver in a similar way.

Conclusion

You can program the finite difference method in a simple way: write down difference equations for a specific problem, enter coefficients in the program, and call the SLAE solution function.

It is more productive to develop a common solver that can be tested on problems with a known solution.