Soccer ball and fullerenes

One of the most beautiful mathematical results can be safely considered the Euler theorem, which first appeared in the journal of the Petersburg Academy of Sciences in the works of Leonhard Euler “Elements of the theory of bodies” and “Proof of some remarkable properties to which bodies bounded by flat faces”.

Euler's theorem. Let be $$${\ rm B}$- the number of vertices of a convex polyhedron, $$${\ rm P}$- the number of its edges and $$$\ Gamma$- the number of faces. Then the equality is true

$$

$${\ rm B} - {\ rm P} + \ Gamma = 2.$$

Number $$$\ chi = {\ rm B} - {\ rm P} + \ Gamma$is called the Euler characteristic of a polyhedron. It is easy to calculate the Euler characteristic for some familiar polyhedra.

Polyhedron	$$${\ rm B}$	$$${\ rm P}$	$$$\ Gamma$	$$$\ chi$
Tetrahedron	four	6	four	2
Cube	eight	12	6	2
Octahedron	6	12	eight	2

Proof of Euler's theorem can be found here .

Let's use Euler's theorem to establish some interesting facts. Look at the image of a soccer ball.
')

Question: how many pentagons do you need to sew a ball? Let be $$$x$- the number of hexagons, and $$$y$- the number of pentagons. Let's apply the Euler theorem to our soccer ball:

$$

$${\ rm B} - {\ rm P} + \ Gamma = 2,$$

Where $$${\ rm B} = \ frac {6x + 5y} {3}$, $$${\ rm P} = \ frac {6x + 5y} {2}$, but $$$\ Gamma = x + y$. The formulas for the number of vertices, edges and faces are easily obtained from the observation that each vertex falls on three faces, and only two faces intersect on each edge. Substituting the values ​​in the formula, you get the answer: $$$y = 12$. Variable $$$x$is excluded from the equation, i.e. the number of hexagons can be anything. The following picture shows a ball made from pentagons alone. How many of them?

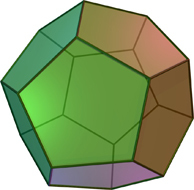
This polyhedron is called the dodecahedron and is one of the five regular polyhedra.

Let's look at another story. Fullerenes are molecular compounds belonging to the class of allotropic forms of carbon and representing convex closed polyhedra composed of an even number of three-coordinated carbon atoms. Fullerens owe their name to engineer and architect Richard Buckminster Fuller, whose geodesic structures are built according to this principle. Initially, this class of compounds was limited only to structures that included only pentagonal and hexagonal faces.

Finally, let's look at the following picture.

Nothing fancy - just a dome made up of hexagons. Now, once again, meditate on Euler's formula and look for the pentagons ahead.

You can find this and many other mathematical topics in the wonderful lectures of Alexey Savvateev or in his book “Mathematics for the Humanities”.