Bitcoin in a nutshell - Cryptography
One of the reasons why Bitcoin continues to attract so much attention is its exceptional “mathematics”. Satoshi Nakamoto managed to create a system that is able to function in the complete absence of trust between its members. All interactions are based on rigorous mathematics, no human factor - this was what the idea was revolutionary in, and not in the peer-to-peer network, as many think. Therefore, I decided to devote the first chapter to Bitcoin’s mathematical foundations.
Below I will try to explain to you the most basic things - elliptic curves, ECC, private / public keys, and so on. If possible, I will illustrate my words with code examples, mostly in Python 2.7, if something is not clear, ask in the comments.

')
As I said above, cryptography is a fundamental part of Bitcoin. Without it, nothing would have worked, so you need to start from here.
Bitcoin uses the so-called elliptic curve cryptography (ECC ). It is based on some special function - an elliptic curve (not to be confused with an ellipse). What is this function and why is it so remarkable, I will tell you further.
If on the fingers, then the elliptic curve is an outwardly rather simple function, usually written in the form of the so-called Weierstrass form:
Depending on the values of the parameters and
and  The graph of this function may look different:
The graph of this function may look different:

Script for drawing graphics in Python:
If you believe the wiki, then for the first time this feature appeared in the writings of Diophantus, and later, in the 17th century, Newton himself became interested in it. His research led in many respects to the formulas for adding points on an elliptic curve, which we will now become acquainted with. Here and in the following we will consider some elliptic curve. .
.
Let there be two points . Their sum is called point
. Their sum is called point  which in the simplest case is defined as follows: let's draw a straight line through
which in the simplest case is defined as follows: let's draw a straight line through  and
and  - she will cross the curve
- she will cross the curve  at a single point let's call it
at a single point let's call it  . Exchanging
. Exchanging  point coordinate
point coordinate  on the opposite sign, we get a point
on the opposite sign, we get a point  which we will call the sum
which we will call the sum  and
and  , i.e
, i.e  .
.
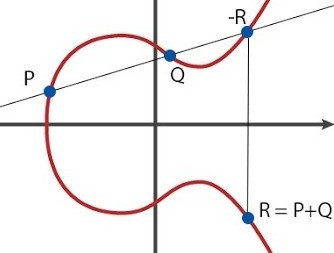
I consider it necessary to note that we are introducing such an operation of addition - if you add points in the usual sense, that is, by adding the corresponding coordinates, you will get a completely different point) which most likely has nothing to do with
which most likely has nothing to do with  or
or  and generally does not lie on the curve
and generally does not lie on the curve  .
.
The most savvy have already wondered - what will happen if, for example, we draw a line through two points that have coordinates of the form?) and
and ) , that is, the straight line passing through them will be parallel to the axis of ordinates (the third frame in the picture below).
, that is, the straight line passing through them will be parallel to the axis of ordinates (the third frame in the picture below).
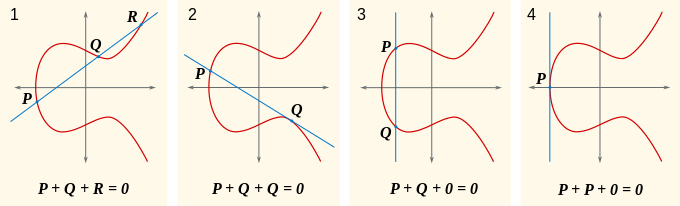
It is easy to see that in this case there is no third intersection with the curve. which we called
which we called  . In order to avoid this incident, we introduce the so-called point in infinity (point of infinity), usually denoted
. In order to avoid this incident, we introduce the so-called point in infinity (point of infinity), usually denoted  or simply
or simply  , like on a picture. And we will say that in the absence of intersection
, like on a picture. And we will say that in the absence of intersection  .
.
Of particular interest to us is the case when we want to add a point to itself (2 frame, point ). In this case, simply draw a tangent to the point.
). In this case, simply draw a tangent to the point.  and reflect the resulting intersection point with respect to
and reflect the resulting intersection point with respect to  .
.
Now, with a flick of the wrist, you can enter the operation of multiplying a point by some number. As a result, we get a new point.
number. As a result, we get a new point.  , i.e
, i.e  time. With the picture, everything should become generally clear:
time. With the picture, everything should become generally clear:
The ECC uses exactly the same curve, only viewed over some finite field.
 - Prime number. I.e
- Prime number. I.e
%0A)
All the named properties (addition, multiplication, point in infinity) for such a function remain in force, although if you try to draw this function, then it will resemble the usual elliptic curve only remotely (at best). And the concept of “tangent to a function at a point” generally loses all meaning, but that’s okay. Here is an example function for
for  :
:
But for , there is generally an almost chaotic set of points. The only thing that still reminds of the origin of this graph is symmetry about the axis
, there is generally an almost chaotic set of points. The only thing that still reminds of the origin of this graph is symmetry about the axis  .
.

PS If you are interested, as in the case of a curve over a finite field, calculate the coordinates of a point) knowing the coordinates
knowing the coordinates ) and
and ) - you can look through “An introduction to Bitcoin, Elliptic Curves and the Mathematics of ECDSA” by N. Mistry , everything is detailed there, it is enough to know mathematics at the grade 8 level.
- you can look through “An introduction to Bitcoin, Elliptic Curves and the Mathematics of ECDSA” by N. Mistry , everything is detailed there, it is enough to know mathematics at the grade 8 level.
PPS In case my examples did not satisfy your inquiring mind, here is a website for drawing curves of all sorts, experiment.
Returning to Bitcoin, it uses the SECP256k1 curve. She has a look and viewed over the field
and viewed over the field  where
where  - a very large prime number, namely
- a very large prime number, namely  .
.
Also for SECP256k1 the so-called base point is defined, it’s also a generator point - this is just a point, as a rule, denoted lying on a given curve. It is needed to create a public key, which will be described below.
lying on a given curve. It is needed to create a public key, which will be described below.
A simple example: using Python, check if a dot belongs) curve SECP256k1
curve SECP256k1
The general idea is this: Alice wants to translate 1 BTC to Bob. To do this, it creates a message like:
Then Alice takes her private key (for now, you can assume that this is a number known only to Alice), a hash of the message, and a function like) . At the output, she receives the signature of her message - in the case of ECDSA it will be a pair of integers, for other algorithms the signature may look different. After that, it sends to all members of the network the original message, signature and its public key.
. At the output, she receives the signature of her message - in the case of ECDSA it will be a pair of integers, for other algorithms the signature may look different. After that, it sends to all members of the network the original message, signature and its public key.
As a result, each Vasya, if he wishes, will be able to take this trinity, a function of the form) and check whether the owner of the private key really signed this message or not. And if everyone inside the network knows that
and check whether the owner of the private key really signed this message or not. And if everyone inside the network knows that  belongs to Alice, it can be understood, she sent the money or someone tries to do it on her behalf.
belongs to Alice, it can be understood, she sent the money or someone tries to do it on her behalf.
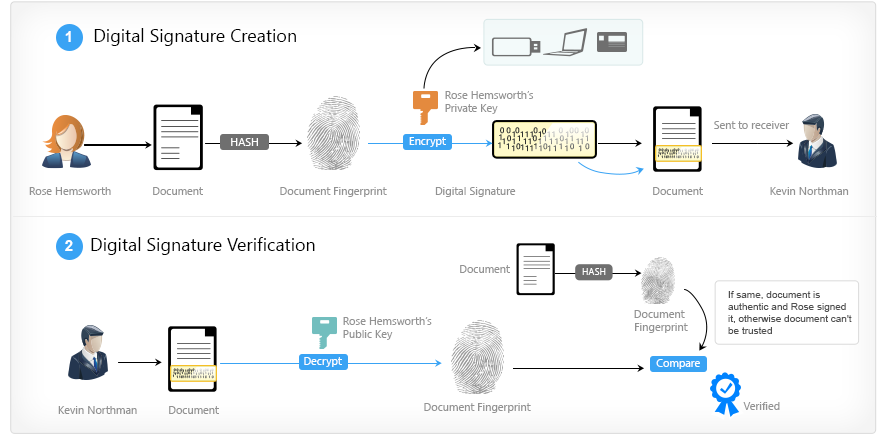
Moreover, suppose there is a person standing between Alice and the rest of the network. Let him intercept Alice's message and change something in him, literally 1 bit out of a billion. But even in this case, the verification of the signature on the validity) will show that the message has been changed.
will show that the message has been changed.
This is a very important feature for Bitcoin, because the network is distributed . We cannot know in advance who our transaction will go to with the requirement to transfer 1000 BTC. But he will not be able to change it (for example, specify his address as a recipient), because the transaction is signed with your private key, and the rest of the network will immediately realize that there is something wrong.
Ahtung In fact, the process is quite different from the above. Here I just showed on my fingers what a digital signature is and why it is needed. The real algorithm is described in the chapter “Bitcoin in a nutshell - Transactions” .
A private key is a fairly generic term, and different types of private keys can be used in various electronic signature algorithms.
As you may have noticed, Bitcoin uses the ECDSA algorithm — in this case, the private key is some natural 256 bit number, that is, the most common integer from before
before  . Technically, even the number 123456 will be the correct private key, but very soon you will find out that your coins "belong" to you exactly until the attacker has your private key, and values like 123456 are very easy to get through.
. Technically, even the number 123456 will be the correct private key, but very soon you will find out that your coins "belong" to you exactly until the attacker has your private key, and values like 123456 are very easy to get through.
It is important to note that, to date, it is impossible to sort through all the keys because - this is a fantastically large number.
- this is a fantastically large number.
We will try to present it: according to this article , a little less on the whole Earth sand grains. We take advantage of the fact that
sand grains. We take advantage of the fact that  , i.e
, i.e  sand grains. And all the addresses we have
sand grains. And all the addresses we have  , about
, about  .
.
So, we can take all the sand on Earth, turn every grain of sand into a new Earth, in the resulting heap of planets every grain of sand on each planet will be turned into a new Earth again, and the total number of grains of sand will still be orders of magnitude less than the number of possible private keys.
For the same reason, most Bitcoin clients simply take 256 random bits when creating a private key - the probability of a collision is extremely small.
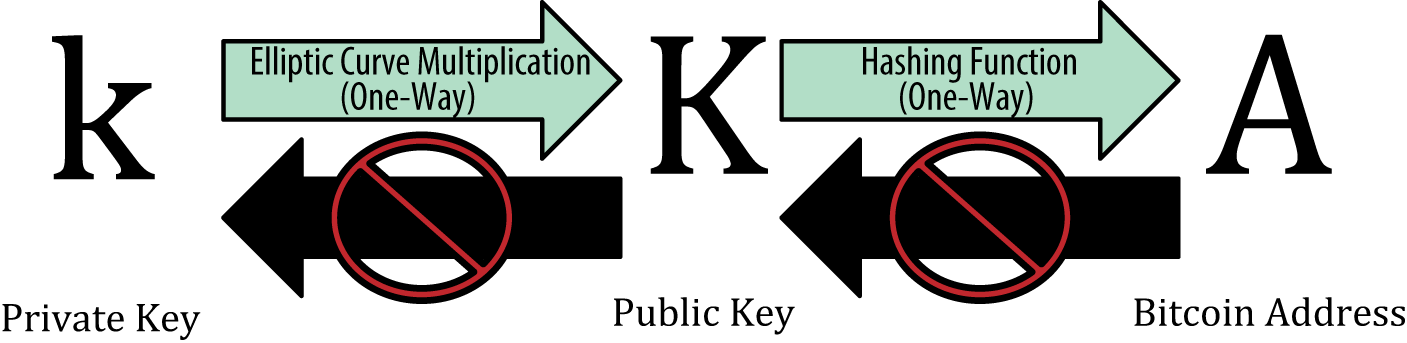
Let be - our private key,
- our private key,  - base point, then the public key
- base point, then the public key  . That is, in fact, the public key is a certain point lying on the SECP256k1 curve.
. That is, in fact, the public key is a certain point lying on the SECP256k1 curve.
Two important nuances. First, it is easy to see that the operation of obtaining a public key is uniquely defined, that is, a single private key always corresponds to a specific private key. Secondly, the inverse operation is computationally difficult and, in the general case, obtaining a private key from the public one can only be done through the first search.
Below you will find out that the exact same connection exists between the public key and the address, only there it is all about the irreversibility of hash functions.
To compile and run use (pre-install libbitcoin):
You can see that the public key formats in the first and second examples are different (at least in length), which I will discuss in more detail below.
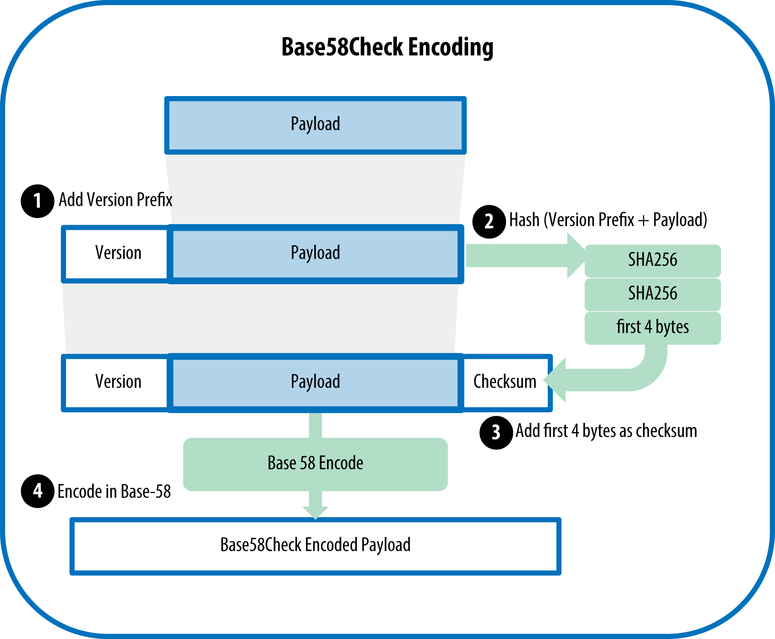
We will meet this encoding all the time throughout the book, so it’s worth understanding how it works and why it is needed at all.
Its essence is to maximally jot down a sequence of bytes in a readable format and, at the same time, make the probability of possible typos even less. I think you understand that in the case of Bitcoin, security is not superfluous. One wrong character and money will go to the address, the keys to which most likely no one will ever find. Here is a comment on this encoding from in base58.h :
The brevity of the record is easiest to implement using the fairly common Base64 encoding, that is, using the base number system 64, where the digits are
The first difference of Base58Check is that the characters
The second difference is the same check . Checksum is added to the end of the line - the first 4 bytes of
The most obvious way to store a private key is to write 256 bits in a heap of zeros and ones. But, probably, any technically literate person understands that it will be much easier to represent the same sequence in the form of 32 bytes, where each byte corresponds to two characters in hexadecimal. Let me remind you that in this case the numbers
Another more progressive format is WIF ( Wallet Import Format ). It is built quite simply:
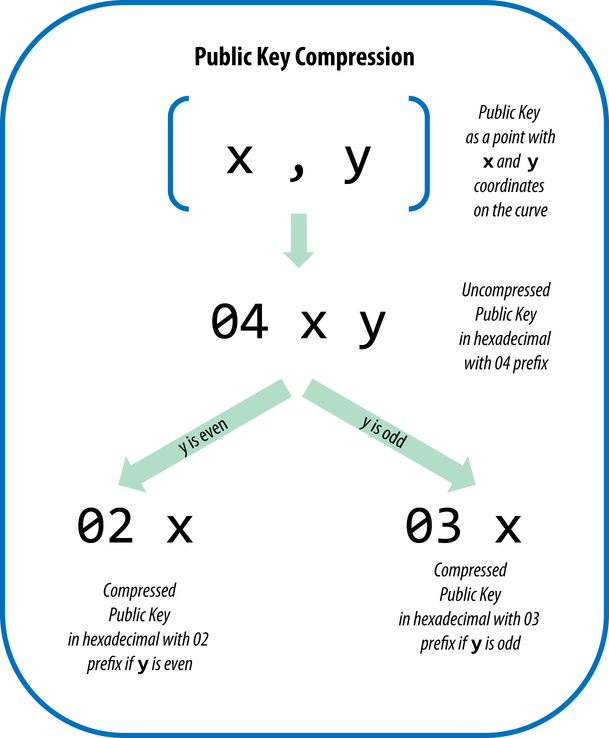
Just in case, I remind you that the public key is just a point on the line SECP256k1. The first and most common variant of his record is uncompressed format, 32 bytes each for X and Y coordinates. To avoid confusion, use the prefix
However, as the name suggests, this is not the best way to store a public key.
You'd be surprised, but the second format is called compressed . Its essence is as follows: the public key is a point on the curve, that is, a pair of numbers satisfying the equation) . So it is possible to write down only the X coordinate, and if we need the Y coordinate, we just solve the equation. Thus, we reduce the size of the public key by almost 50%!
. So it is possible to write down only the X coordinate, and if we need the Y coordinate, we just solve the equation. Thus, we reduce the size of the public key by almost 50%!
The only caveat is that if a point lies on a curve, then for its X coordinate there are obviously two solutions to such an equation (look at the graphs above if in doubt). Usually we would simply keep the sign for the Y coordinate, but when it comes to the function over a finite field, then we need to use the following property: if for the X coordinate there are solutions to the equation, then one of the points will have an even Y coordinate, and the second will be odd (again you can see for yourself).
In the first case, the prefix
As already mentioned, the address is obtained from the public key unambiguously. Moreover, it is impossible to perform the inverse operation, since the cryptographically secure hash functions, RIPEMD160 and SHA256, are used . Here is the algorithm for transferring the public key to the address:
I don’t think you need to know the technical details of exactly how ECDSA signs and verifies messages, anyway you will use ready-made libraries everywhere. The main thing is that you have a general understanding of why this is needed, but if you are still interested in it - look through the Layman's Guide to Elliptic Curve Digital Signatures , there is a beautiful visualization of the whole process below, you can try it yourself.
I have it all, the next chapter: Bitcoin in a nutshell - Transaction .
Below I will try to explain to you the most basic things - elliptic curves, ECC, private / public keys, and so on. If possible, I will illustrate my words with code examples, mostly in Python 2.7, if something is not clear, ask in the comments.

')
Book
- Bitcoin in a nutshell - Cryptography
- Bitcoin in a nutshell - Transaction
- Bitcoin in a nutshell - Protocol
- Bitcoin in a nutshell - Blockchain
- Bitcoin in a nutshell - Mining
Table of content
- Introduction
- Elliptic curve
- Digital signature
- Private key
- Public key
- Formats & address
- Sign
- Verify
- Formats
- Links
Introduction
As I said above, cryptography is a fundamental part of Bitcoin. Without it, nothing would have worked, so you need to start from here.
Bitcoin uses the so-called elliptic curve cryptography (ECC ). It is based on some special function - an elliptic curve (not to be confused with an ellipse). What is this function and why is it so remarkable, I will tell you further.
Elliptic curve
Elliptical curve over field- non-singular cubic curve on the projective plane above
(algebraic closure of the field
), given by a 3rd degree equation with coefficients from the field
and "point at infinity" - Wikipedia
If on the fingers, then the elliptic curve is an outwardly rather simple function, usually written in the form of the so-called Weierstrass form:
Depending on the values of the parameters

Script for drawing graphics in Python:
import numpy as np import matplotlib.pyplot as plt def main(): a = -1 b = 1 y, x = np.ogrid[-5:5:100j, -5:5:100j] plt.contour(x.ravel(), y.ravel(), pow(y, 2) - pow(x, 3) - x * a - b, [0]) plt.grid() plt.show() if __name__ == '__main__': main() If you believe the wiki, then for the first time this feature appeared in the writings of Diophantus, and later, in the 17th century, Newton himself became interested in it. His research led in many respects to the formulas for adding points on an elliptic curve, which we will now become acquainted with. Here and in the following we will consider some elliptic curve.
Let there be two points

I consider it necessary to note that we are introducing such an operation of addition - if you add points in the usual sense, that is, by adding the corresponding coordinates, you will get a completely different point
The most savvy have already wondered - what will happen if, for example, we draw a line through two points that have coordinates of the form?

It is easy to see that in this case there is no third intersection with the curve.
Of particular interest to us is the case when we want to add a point to itself (2 frame, point
Now, with a flick of the wrist, you can enter the operation of multiplying a point by some

Elliptic curve over a finite field
The ECC uses exactly the same curve, only viewed over some finite field.
All the named properties (addition, multiplication, point in infinity) for such a function remain in force, although if you try to draw this function, then it will resemble the usual elliptic curve only remotely (at best). And the concept of “tangent to a function at a point” generally loses all meaning, but that’s okay. Here is an example function

But for

PS If you are interested, as in the case of a curve over a finite field, calculate the coordinates of a point
PPS In case my examples did not satisfy your inquiring mind, here is a website for drawing curves of all sorts, experiment.
SECP256k1
Returning to Bitcoin, it uses the SECP256k1 curve. She has a look
Also for SECP256k1 the so-called base point is defined, it’s also a generator point - this is just a point, as a rule, denoted
A simple example: using Python, check if a dot belongs
>>> p = 115792089237316195423570985008687907853269984665640564039457584007908834671663 >>> x = 55066263022277343669578718895168534326250603453777594175500187360389116729240 >>> y = 32670510020758816978083085130507043184471273380659243275938904335757337482424 >>> (x ** 3 + 7) % p == y**2 % p True Digital signature
Electronic signature (EDS), Electronic digital signature (EDS) - the attribute of an electronic document obtained as a result of cryptographic transformation of information using the private key of the signature and allowing to verify the absence of distortion of information in the electronic document from the moment of signature formation (integrity) signatures (authorship), and in case of successful verification, confirm the fact of signing an electronic document (non-repudiation) - Wikipedia
The general idea is this: Alice wants to translate 1 BTC to Bob. To do this, it creates a message like:
{ "from" : 1FXySbm7jpJfHEJRjSNPPUqnpRTcSuS8aN, // Alice's address "to" : 1Eqm3z1yu6D4Y1c1LXKqReqo1gvZNrmfvN, // Bob's address "amount" : 1 // Send 1 BTC } Then Alice takes her private key (for now, you can assume that this is a number known only to Alice), a hash of the message, and a function like
As a result, each Vasya, if he wishes, will be able to take this trinity, a function of the form

Moreover, suppose there is a person standing between Alice and the rest of the network. Let him intercept Alice's message and change something in him, literally 1 bit out of a billion. But even in this case, the verification of the signature on the validity
This is a very important feature for Bitcoin, because the network is distributed . We cannot know in advance who our transaction will go to with the requirement to transfer 1000 BTC. But he will not be able to change it (for example, specify his address as a recipient), because the transaction is signed with your private key, and the rest of the network will immediately realize that there is something wrong.
Ahtung In fact, the process is quite different from the above. Here I just showed on my fingers what a digital signature is and why it is needed. The real algorithm is described in the chapter “Bitcoin in a nutshell - Transactions” .
Private key
A private key is a fairly generic term, and different types of private keys can be used in various electronic signature algorithms.
As you may have noticed, Bitcoin uses the ECDSA algorithm — in this case, the private key is some natural 256 bit number, that is, the most common integer from
It is important to note that, to date, it is impossible to sort through all the keys because
We will try to present it: according to this article , a little less on the whole Earth
So, we can take all the sand on Earth, turn every grain of sand into a new Earth, in the resulting heap of planets every grain of sand on each planet will be turned into a new Earth again, and the total number of grains of sand will still be orders of magnitude less than the number of possible private keys.
For the same reason, most Bitcoin clients simply take 256 random bits when creating a private key - the probability of a collision is extremely small.
Python
>>> import random >>> private_key = ''.join(['%x' % random.randrange(16) for x in range(0, 64)]) >>> private_key '9ceb87fc34ec40408fd8ab3fa81a93f7b4ebd40bba7811ebef7cbc80252a9815' >>> # or >>> import os >>> private_key = os.urandom(32).encode('hex') >>> private_key '0a56184c7a383d8bcce0c78e6e7a4b4b161b2f80a126caa48bde823a4625521f' Python, ECDSA
>>> import binascii >>> import ecdsa # sudo pip install ecdsa >>> private_key = ecdsa.SigningKey.generate(curve=ecdsa.SECP256k1) >>> binascii.hexlify(private_key.to_string()).decode('ascii').upper() u'CE47C04A097522D33B4B003B25DD7E8D7945EA52FA8931FD9AA55B315A39DC62' Bitcoin-cli
$ bitcoin-cli getnewaddress 14RVpC4su4PzSafjCKVWP2YBHv3f6zNf6U $ bitcoin-cli dumpprivkey 14RVpC4su4PzSafjCKVWP2YBHv3f6zNf6U L3SPdkFWMnFyDGyV3vkCjroGi4zfD59Wsc5CHdB1LirjN6s2vii9 Public key
Let be
Two important nuances. First, it is easy to see that the operation of obtaining a public key is uniquely defined, that is, a single private key always corresponds to a specific private key. Secondly, the inverse operation is computationally difficult and, in the general case, obtaining a private key from the public one can only be done through the first search.
Below you will find out that the exact same connection exists between the public key and the address, only there it is all about the irreversibility of hash functions.

Python, ECDSA
>>> import binascii >>> import ecdsa >>> private_key = ecdsa.SigningKey.generate(curve=ecdsa.SECP256k1) >>> public_key = private_key.get_verifying_key() >>> binascii.hexlify(public_key.to_string()).decode('ascii').upper() u'D5C08F1BFC9C26A5D18FE9254E7923DEBBD34AFB92AC23ABFC6388D2659446C1F04CCDEBB677EAABFED9294663EE79D71B57CA6A6B76BC47E6F8670FE759D746' C ++, libbitcoin
#include <bitcoin/bitcoin.hpp> #include <iostream> int main() { // Private key bc::ec_secret secret = bc::decode_hash( "038109007313a5807b2eccc082c8c3fbb988a973cacf1a7df9ce725c31b14776"); // Get public key bc::ec_point public_key = bc::secret_to_public_key(secret); std::cout << "Public key: " << bc::encode_hex(public_key) << std::endl; } To compile and run use (pre-install libbitcoin):
$ g++ -o public_key <filename> $$(pkg-config --cflags --libs libbitcoin) $ ./public_key Public key: 0202a406624211f2abbdc68da3df929f938c3399dd79fac1b51b0e4ad1d26a47aa You can see that the public key formats in the first and second examples are different (at least in length), which I will discuss in more detail below.
Formats & address
Base58Check encoding
We will meet this encoding all the time throughout the book, so it’s worth understanding how it works and why it is needed at all.
Its essence is to maximally jot down a sequence of bytes in a readable format and, at the same time, make the probability of possible typos even less. I think you understand that in the case of Bitcoin, security is not superfluous. One wrong character and money will go to the address, the keys to which most likely no one will ever find. Here is a comment on this encoding from in base58.h :
// Why base-58 instead of standard base-64 encoding? // - Don't want 0OIl characters that look the same in some fonts and // could be used to create visually identical looking account numbers. // - A string with non-alphanumeric characters is not as easily accepted as an account number. // - E-mail usually won't line-break if there's no punctuation to break at. // - Doubleclicking selects the whole number as one word if it's all alphanumeric.
The brevity of the record is easiest to implement using the fairly common Base64 encoding, that is, using the base number system 64, where the digits are
0,1,...,9 , the letters az and AZ - this gives 62 characters, the remaining two can be anything, depending on the implementation.The first difference of Base58Check is that the characters
0,O,l,I removed in case someone decides to confuse them. It turns out 58 characters, you can check b58 = '123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz' def base58encode(n): result = '' while n > 0: result = b58[n%58] + result n /= 58 return result # print "Base58 encode for '123123':", base58encode(123123) # # Base58 encode for '123123': dbp The second difference is the same check . Checksum is added to the end of the line - the first 4 bytes of
SHA256(SHA256(str)) . Well, you still need to add as many units to the beginning as there were leading zeros before encoding in base58, this is already a matter of technique. import hashlib def base58encode(n): b58 = '123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz' result = '' while n > 0: result = b58[n % 58] + result n /= 58 return result # Will be used to decode raw bytes and then encode them to the base58 def base256decode(s): result = 0 for c in s: result = result * 256 + ord(c) return result def countLeadingZeroes(s): count = 0 for c in s: if c == '\0': count += 1 else: break return count def base58CheckEncode(prefix, payload): s = chr(prefix) + payload checksum = hashlib.sha256(hashlib.sha256(s).digest()).digest()[0:4] result = s + checksum return '1' * countLeadingZeroes(result) + base58encode(base256decode(result)) 
Private key formats
The most obvious way to store a private key is to write 256 bits in a heap of zeros and ones. But, probably, any technically literate person understands that it will be much easier to represent the same sequence in the form of 32 bytes, where each byte corresponds to two characters in hexadecimal. Let me remind you that in this case the numbers
0,1,...,9 and the letters A,B,C,D,E,F . I used this format in the examples above, for beauty it is sometimes separated by spaces. E9 87 3D 79 C6 D8 7D C0 FB 6A 57 78 63 33 89 F4 45 32 13 30 3D A6 1F 20 BD 67 FC 23 3A A3 32 62 Another more progressive format is WIF ( Wallet Import Format ). It is built quite simply:
- We take a private key, for example
0C28FCA386C7A227600B2FE50B7CAE11EC86D3BF1FBE471BE89827E19D72AA1D - We write it in Base58Check with the prefix
0x80. Everything.
private_key = '0a56184c7a383d8bcce0c78e6e7a4b4b161b2f80a126caa48bde823a4625521f' def privateKeyToWif(key_hex): return base58CheckEncode(0x80, key_hex.decode('hex')) # print "Private key in WIF format:", privateKeyToWif(private_key) # # Private key in WIF format: 5HtqcFguVHA22E3bcjJR2p4HHMEGnEXxVL5hnxmPQvRedSQSuT4 Public key formats
Just in case, I remind you that the public key is just a point on the line SECP256k1. The first and most common variant of his record is uncompressed format, 32 bytes each for X and Y coordinates. To avoid confusion, use the prefix
0x04 and that 65 bytes. import ecdsa private_key = '0a56184c7a383d8bcce0c78e6e7a4b4b161b2f80a126caa48bde823a4625521f' def privateKeyToPublicKey(s): sk = ecdsa.SigningKey.from_string(s.decode('hex'), curve=ecdsa.SECP256k1) vk = sk.verifying_key return ('\04' + sk.verifying_key.to_string()).encode('hex') uncompressed_public_key = privateKeyToPublicKey(private_key) # print "Uncompressed public key: {}, size: {}".format(uncompressed_public_key, len(uncompressed_public_key) / 2) # # Uncompressed public key: 045fbbe96332b2fc2bcc1b6a267678785401ee3b75674e061ca3616bbb66777b4f946bdd2a6a8ce419eacc5d05718bd718dc8d90c497cee74f5994681af0a1f842, size: 65 However, as the name suggests, this is not the best way to store a public key.
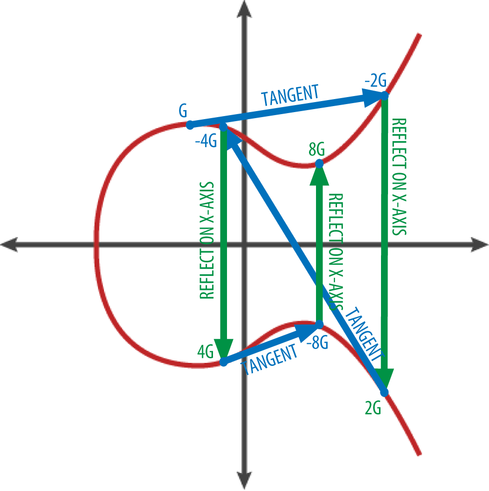
You'd be surprised, but the second format is called compressed . Its essence is as follows: the public key is a point on the curve, that is, a pair of numbers satisfying the equation
The only caveat is that if a point lies on a curve, then for its X coordinate there are obviously two solutions to such an equation (look at the graphs above if in doubt). Usually we would simply keep the sign for the Y coordinate, but when it comes to the function over a finite field, then we need to use the following property: if for the X coordinate there are solutions to the equation, then one of the points will have an even Y coordinate, and the second will be odd (again you can see for yourself).
In the first case, the prefix
0x02 , in the second - 0x03 . Here is an illustration of the process:
Address
As already mentioned, the address is obtained from the public key unambiguously. Moreover, it is impossible to perform the inverse operation, since the cryptographically secure hash functions, RIPEMD160 and SHA256, are used . Here is the algorithm for transferring the public key to the address:
- Take a private key, for example
45b0c38fa54766354cf3409d38b873255dfa9ed3407a542ba48eb9cab9dfca67 - We obtain from it the public key in uncompressed format, in this case
04162ebcd38c90b56fbdb4b0390695afb471c944a6003cb334bbf030a89c42b584f089012beb4842483692bdff9fcab8676fed42c47bffb081001209079bbcb8db. - We consider
RIPEMD160(SHA256(public_key)), it turns out5879DB1D96FC29B2A6BDC593E67EDD2C5876F64C - We translate the result into Base58Check with the prefix
0x00-17JdJpDyu3tB5GD3jwZP784W5KbRdfb84X. This is the address.
def pubKeyToAddr(s): ripemd160 = hashlib.new('ripemd160') ripemd160.update(hashlib.sha256(s.decode('hex')).digest()) return base58CheckEncode(0, ripemd160.digest()) def keyToAddr(s): return pubKeyToAddr(privateKeyToPublicKey(s)) # print keyToAddr("45b0c38fa54766354cf3409d38b873255dfa9ed3407a542ba48eb9cab9dfca67") # # '17JdJpDyu3tB5GD3jwZP784W5KbRdfb84X' Sign & verify
I don’t think you need to know the technical details of exactly how ECDSA signs and verifies messages, anyway you will use ready-made libraries everywhere. The main thing is that you have a general understanding of why this is needed, but if you are still interested in it - look through the Layman's Guide to Elliptic Curve Digital Signatures , there is a beautiful visualization of the whole process below, you can try it yourself.
I have it all, the next chapter: Bitcoin in a nutshell - Transaction .
Links
Source: https://habr.com/ru/post/319868/
All Articles