Duplo Railroad Tycoon: Synthesis of the rail network with maximum coverage

Santa Claus brought the children Duplo railway. Rail segments are very easily interconnected, and you can build some small, most likely just a closed path, put the station and watch the train running in a circle. Sometimes it stops and the baby must “fill” the locomotive from the column, after which the locomotive will go again.

Here is an example of the simplest path:



I was very bored with this train, the circle after the third, and I went again to dig into the Thingiverse, in order to try to use a 3D printer for something useful one hundred thousand times. And suddenly I find a segment-arrow there just for the Duplo locomotive.
')
The arrow works like this: it has three inputs and outputs, let's call them first, second and third. If a train enters the first or second node, then it always leaves the arrow through the third. In this case, the arrow switches to the corresponding node (i.e., if entered through the first, it switches to the first, if through the second, then to the second). But if he enters the third node, the output depends on the state of the arrow and he can leave both through the first and second. Those.:

'1' -> '3' (the arrow translates to '1')
'2' -> '3' (the arrow translates to '2')
'3' -> if the arrow is on '1', then '1', otherwise '2'

I printed out a couple of such shooters, and began to collect the "normal" railway. But everything worked out somehow sadly - the locomotive traveled only along part of the way, stuck on some ring, and did not want to leave it.

Problem one (simple): How many shooter segments should there be in a network so that all nodes are interconnected? The road must be continuous and not have dead ends.


But podnapryagis, for the simplest version, I solved the problem in a few days. A friend who came to visit decided it in 5 minutes without straining :)

Denote each arrow with a letter, nodes as in the example above. Those. there are nodes in our network ['a1', 'a2', 'a3', 'b1', 'b2', 'b3'].


And what if you take more shooters? Hmm, if I thought so much about a simple solution, then I’m obviously not going to master it anymore. But master the computer! But how to get to this task? I struggled for a few days, trying to add some depth search to this, and I almost left everything, when suddenly I had the idea to write a solution on a piece of paper.

I just broke the whole track into steps:

Current state → Go to arrow → Go to connecting segment → Remember new state of arrows

Those. For the solution above, the transitions will be as follows (the state of the arrows: a3-> a1; b3-> b1):

a1 -> a3 -> b3 (a3-> a1; b3-> b1)
b3 -> b1 -> b2 (a3-> a1; b3-> b1)
b2 -> b3 -> a3 (a3-> a1; b3-> b2) ## note that the arrow b3 has switched

Further simple:

• We generate all possible road configurations for a given number of arrows.
• For each road:
  
  • We run the train 10 times and count the number of passage for each node
  • If there are nodes with 0 or 1 passage, then this means the system after entering the mode fell into an infinite loop
  • If there are no such nodes, then the train is safely worn all the way, which is what we need!

So simple, that I fought my head on the table for two days and eventually went to ask for advice on stackoverflow, where I was given a number of solutions on a silver platter in a matter of minutes.

Track Generator (I will not declare the task and put it in the spoiler - for someone like me it can be a very cruel joke, but try it yourself for the sake of interest to solve):

def getTrack(l): # recursion anchor, basic case: # when we have 2 nodes only one pair is possible if len(l) == 2: yield [tuple(l)] else: # Pair the first node with all the others for i in range(1, len(l)): # Current pair pair1 = [(l[0], l[i])] # Combine it with all pairs among the remaining nodes remaining = l[1:i] + l[i+1:] for otherPairs in getTrack2(remaining, 1): yield pair1 + otherPairs 

Reshalk tracks:

 def solveTrack(track): #        nodeCount = {} for n in nodes: nodeCount[n] = 0 railTr = None jointTr = 'a1' while True: pos = jointTr #  nodeCount[pos] += 1 #  railTr = getTransition(track, pos) #    (    ) nodeCount[railTr] += 1 #    jointTr = tj[railTr] #   (    ,        ) if railTr[1] in ['1','2']: ##  tj[railTr[0]+'3'] = railTr if max(nodeCount.values()) > nodesTrace and min(nodeCount.values()) < 3: #       nodesTrace ,     .   -   -     . #print "Infinite cycle detected" break #sol = "{}\t{}\t{}\t{}\t{}".format(pos, railTr, jointTr, tj['a3'], tj['b3']) #print sol if max(nodeCount.values()) > nodesTrace * 1.5: print "-------------------------------------------------------\n" print "Simulation complete!" print '\nNodes: ', nodeCount, "\n" print "Solution: ", track break return 

It remains only to specify a list of nodes for the input data, transitions between nodes of the arrow and begin the search for a solution! Hooray!

 tj = {} #  nodes = [] #  ##create joints transition table for jt in range(nJoints): tj[idxs[jt]+'1'] = idxs[jt]+'3' tj[idxs[jt]+'2'] = idxs[jt]+'3' tj[idxs[jt]+'3'] = idxs[jt]+'1' nodes.extend((idxs[jt]+'1', idxs[jt]+'2', idxs[jt]+'3')) 

Hmm, but there is no solution near the road with four arrows. And with six (I waited a few hours) - also not. That's all. The dream is over.

Although. But what if you make only a part of the arrows switchable and freeze the rest? For example:

 if railTr[0] in idxs[:nSwitchableJoints]: ## nSwitchableJoints -     if railTr[1] in ['1','2']: ##  tj[railTr[0]+'3'] = railTr 

And voila - there are solutions and there are a lot of them! I tried to choose something prettier :)


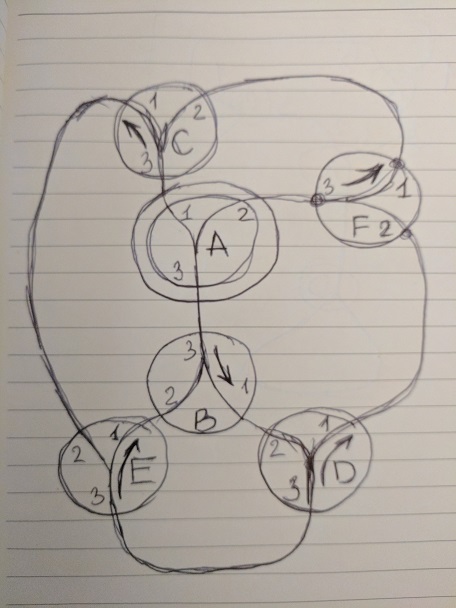
Here, only the arrow 'a' is switchable, the other three are always resolved to one.
This track corresponds to the solution:

 [('a1', 'c3'), ('a2', 'f3'), ('a3', 'b3'), ('b1', 'd2'), ('b2', 'e1'), ('c1', 'e2'), ('c2', 'f1'), ('d1', 'f2'), ('d3', 'e3')] nSwitchableJoints = 1 

That's all, bye!