Common mistakes beginners work with images

Digital image processing is a very interesting area, but it is fraught with many pitfalls that beginners constantly stumble upon. We are actively attracting students to participate in grants and projects, but when we tried to give students real tasks that require the implementation of new image processing algorithms, we were horrified by their children's mistakes.

Therefore, before setting full-fledged tasks, we began to give students a number of practical tasks for implementing standard image processing algorithms: basic image operations (rotate, blur), convolution, interpolation using simple filters (bilinear, bicubic), directional interpolation, selection of boundaries using an algorithm Canny, detect key points, etc. The programming language could be any, however, when performing tasks, the use of third-party libraries is not allowed, with the exception of reading and writing images. This is due to the fact that assignments are educational in nature, self-realization of algorithms is a good practice in programming and allows you to understand how the methods work from the inside.

This article describes the most common mistakes made by students in performing practical tasks in image processing. Images are ordinary, no exotics such as 16-bit color depth, panchromaticity and 3D images are present.

Error 1. Working with pixels using system objects Bitmap, HBITMAP and the like to store images

These objects are designed to interact with the graphics subsystem (drawing primitives and text, output to the screen) and do not provide direct access to the section of memory in which image pixels are stored. Access to the pixels is carried out using the functions GetPixel and SetPixel. Calling these functions is very expensive - two to three orders of magnitude slower than direct access to pixels. The temptation is especially great to do this in C #, where the Bitmap type is available out of the box.

Solution: use these classes only for reading from a file, writing to a file and outputting to the screen, otherwise working with classes that have effective access to the pixels.

Note: in some cases in Windows it is convenient to work with DIB (device independent bitmap): there is also direct access to the pixels, and the possibility of displaying on the screen, minus is a restriction on the type of pixel.

Mistake 2. Using image libraries with no image processing experience.

The use of libraries is fraught with misunderstanding of the work of algorithms and further difficulties in solving practical problems that require the development of their own algorithms, which are not found in libraries. I came across well-programmed students who could not even implement elementary operations such as convolutions: either they couldn’t connect the library, it didn’t work that well, but the mind was not enough to write a function of 10 lines.

Solution: do not use third-party libraries, but write your own classes for working with images and independently implement the basic algorithms. This is especially useful for those who do not have sufficient programming experience. It’s better to break a bike several times than to overwhelm a whole project because of silly mistakes.

Error 3. Loss in accuracy when rounding

As a result of the application of various image processing algorithms, intermediate results with real type arise. Example: almost any averaging filter, for example, a Gaussian filter. Reduction of results to the byte type leads to the introduction of an additional error and less accurate operation of the algorithms.

Below is an example of the operation of the Canny contour detection algorithm, one of the components of which is the calculation of the gradient modulus. On the left - the gradient module after the calculation is stored in the float type, on the right - rounded to byte.

It is easy to see that when rounding the contours become ragged.

Solution: if accuracy is critical for the algorithm, then use the float type instead of byte to store pixel values, do not prematurely optimize - first achieve the normal operation of the float algorithm and then think about where you can use byte so that quality does not decrease.

Note: the speed of modern processors with real numbers is comparable to integers. In some cases, the compiler may use automatic vectorization, which will lead to faster code with float. Also, the code with float can be faster with a large number of byte-float transformations, rounding and clipping. But the use of double is rarely justified, but a hodgepodge of float and double is generally the result of a misunderstanding of the types and principles of working with them.

Using integer types (byte, int16, uint16) is especially effective when using vector operations, when memory access speed becomes a bottleneck.

Error 4. Out of pixel values ​​out of range [0, 255]

You have no problems with accuracy and you still want to use the byte type to store pixel values? Then another problem arises: many operations, such as bicubic interpolation or sharpening, lead to the appearance of values ​​outside the specified range. If this fact is not taken into account, an effect appears, called wrapping: the value 260 turns into 4, and –3 - into 253. Bright points and lines appear on a dark background and dark ones - on a light (on the left - the correct implementation, on the right - with an error) .

Solution: when performing intermediate operations, check the range of possible values ​​at each step, and when converting to byte type, check that the range is out of range, for example:

unsigned char clamp(float x) { return x < 0.0f ? 0 : (x > 255.0f ? 255 : (unsigned char)x); } 

Error 5. Loss of values ​​as a result of reduction to the range [0, 255]

Do you prefer to work with the byte type and use the clamp function? Are you sure that you have nothing to lose, as in the case of rounding?

I saw in practice how students, when calculating a derivative or applying a Sobel filter, thus lost negative values.

Solution: use types of sufficient size to store intermediate results, and the clamp function only to save to a file or display on the screen. To visualize the derivative, add 128 to the pixel value, or take the module.

Error 6. Wrong order to bypass pixels of the image, resulting in slowing down the program

Memory in the computer is one-dimensional. Two-dimensional images are stored in memory as one-dimensional arrays. Usually they are written line by line: first comes the 0th line, then the 1st, and so on.
Serial memory access is faster than random access. This is due to the work of the processor cache, which places data from the memory into the cache in large blocks, for example, 64 bytes for modern processors. Several horizontally adjacent pixels fall into this block at once. This means that when referring to subsequent pixels in the same row, the access speed will be higher than to subsequent pixels in the column.

Solution: Bypassing the image must be done in such a way that the memory access is consistent: in the external loop, the bypass is performed vertically, and in the internal loop - horizontally:

 for (int y = 0; y < image.Height(); y++) for (int x = 0; x < image.Width(); x++) ... 

Note: In different languages, the way of representing multidimensional arrays in memory may be different. Keep this in mind.

Mistake 7. Confusion with width and height.

The classic problem: testing is either absent or is carried out only on square images; in the field, when working with rectangular images, the array goes beyond the boundary.

Solution: do not forget about testing! I propose not to raise the argument about TDD: its use is a personal matter for everyone.

Error 8. Refusal of abstractions

Fear of producing entities is a typical mistake for beginners, it leads to problems with readability and perception of the code. There are many examples here.

1. getPixel(x, y) pixels by directly calculating the indices in the array instead of using the getPixel(x, y) and setPixel(x, y) methods. In addition to convenience, in these methods you can check and correctly handle the overrun of the image. For example, not to give an error, but to extrapolate image values.

 b1 = (float)0.25 * ( w1 - 1) * (w1 - 2) * (w1 + 1) * (h1 - 1) * (h1 - 2) * (h1 + 1); b2 = -(float)0.25 * w1 * (w1 + 1) * (w1 - 2) * (h1 - 1) * (h1 - 2) * (h1 + 1); b3 = -(float)0.25 * (w1 - 1) * (w1 - 2) * (w1 + 1) * (h1 + 1) * (h1 - 2); b4 = (float)0.25 * w1 * h1 * (w1 + 1) * (w1 - 2) * (h1 + 1) * (h1 - 2); b5 = -(1 / 12) * w1 * (w1 - 1) * (w1 - 2) * (h1 - 1) * (h1 - 2) * (h1 + 1); b6 = -(1 / 12) * h1 * (w1- 1) * (w1 - 2) * (w1 + 1) * (h1 - 1) * (h1 - 2); b7 = (1 / 12) * w1 * h1 * (w1 + 1) * (w1 - 2) * (h1 + 1) * (h1 - 2); b8 = (1 / 12) * w1 * h1 * (w1- 1) * (w1 - 2) * (h1 - 1) *( h1 - 2); b9 = (1 / 12) * w1 * (w1 - 1) * (w1 + 1) * (h1 - 1) * (h1 - 2) * (h1 + 1); b10 = (1 / 12) * w1 * (w1 - 1) * (w1 - 2) * (w1 + 1) * (h1 - 1) * (h1+ 1); b11 = (1 / 36) * w1 * h1 * (w1 - 1) * (w1 - 2) * (w1 - 1) * (h1 - 2) * (h1- 2); b12 = -(1 / 12) * w1 * h1 * (w1 - 1) * (w1 + 1) * (h1 + 1) * (h1 - 2); b13 = -(1 / 12) * w1 * h1 * (w1 + 1) * (w1 - 2) * (h1 - 1) * (h1 + 1); b14 = -(1 / 36) * w1 * (w1 - 1) * (w1 + 1) * (h1 - 1) * (h1 - 2); b15 = -(1 / 36) * w1 * h1 * (w1 - 1) * (w1 - 2) * (h1 - 1) * (h1 + 1); b16 = (1 / 36) * w1 * h1 * (w1 - 1) * (w1 + 1) * (h1 - 1) * (h1 + 1); image2.rawdata[y1 * image2.Width + x1].b = image1.rawdata[h * image1.Width + w].b * b1 + image1.rawdata[h * image1.Width + w + 1].b * b2 + image1.rawdata[(h + 1) * image1.Width + w].b * b3 + image1.rawdata[(h + 1) * image1.Width + w + 1].b * b4 + image1.rawdata[h * image1.Width + w - 1].b * b5 + image1.rawdata[(h - 1) * image1.Width + w].b * b6 + image1.rawdata[(h + 1) * image1.Width + w - 1].b * b7 + image1.rawdata[(h - 1) * image1.Width + w + 1].b * b8 + image1.rawdata[h * image.Width + w + 2].b * b9 + image1.rawdata[(h + 2) * image1.Width + w].b * b10 + image1.rawdata[(h - 1) * image1.Width + w - 1].b * b11 + image1.rawdata[(h + 1) * image1.Width + w + 2].b * b12 + image1.rawdata[(h + 2) * image1.Width + w + 1].b * b13 + image1.rawdata[(h - 1) * image1.Width + w + 2].b * b14 + image1.rawdata[(h + 2) * image1.Width + w - 1].b * b15 + image1.rawdata[(h + 2) * image1.Width + w + 2].b * b16; image2.rawdata[y1 * image2.Width + x1].g = image1.rawdata[h * image1.Width + w].g * b1 + image1.rawdata[h * image1.Width + w + 1].g * b2 + image1.rawdata[(h + 1) * image1.Width + w].g * b3 + image1.rawdata[(h + 1) * image1.Width + w + 1].g * b4 + image1.rawdata[h * image1.Width + w - 1].g * b5 + image1.rawdata[(h - 1) * image1.Width + w].g * b6 + image1.rawdata[(h + 1) * image1.Width + w - 1].g * b7 + image1.rawdata[(h - 1) * image1.Width + w + 1].g * b8 + image1.rawdata[h * image1.Width + w + 2].g * b9 + image1.rawdata[(h + 2) * image1.Width + w].g * b10 + image1.rawdata[(h - 1) * image1.Width + w - 1].g * b11 + image1.rawdata[(h + 1) * image1.Width + w + 2].g * b12 + image1.rawdata[(h + 2) * image1.Width + w + 1].g * b13 + image1.rawdata[(h - 1) * image1.Width + w + 2].g * b14 + image1.rawdata[(h + 2) * image1.Width + w - 1].g * b15 + image1.rawdata[(h + 2) * image1.Width + w + 2].g * b16; image2.rawdata[y1 * image2.Width + x1].r = image1.rawdata[h * image1.Width + w].r * b1 + image1.rawdata[h * image1.Width + w + 1].r * b2 + image1.rawdata[(h + 1) * image1.Width + w].r * b3 + image1.rawdata[(h + 1) * image1.Width + w + 1].r * b4 + image1.rawdata[h * image1.Width + w - 1].r * b5 + image1.rawdata[(h - 1) * image1.Width + w].r * b6 + image1.rawdata[(h + 1) * image1.Width + w - 1].r * b7 + image1.rawdata[(h - 1) * image1.Width + w + 1].r * b8 + image1.rawdata[h * image1.Width + w + 2].r * b9 + image1.rawdata[(h + 2) * image1.Width + w].r * b10 + image1.rawdata[(h - 1) * image1.Width + w - 1].r * b11 + image1.rawdata[(h + 1) * image1.Width + w + 2].r * b12 + image1.rawdata[(h + 2) * image1.Width + w + 1].r * b13 + image1.rawdata[(h - 1) * image1.Width + w + 2].r * b14 + image1.rawdata[(h + 2) * image1.Width + w - 1].r * b15 + image1.rawdata[(h + 2) * image1.Width + w + 2].r * b16; 

2. Duplication of code when working with color images, leading to errors (see example above). Instead of copy-paste code and replacing r with g and b , it would be enough to use operator overloading. Three times less code, three times clearer.

3. Using two-dimensional arrays instead of creating a separate class for the image.
The problem is that the indexing is unnatural - (y, x) instead of (x, y) , and the dimensions of the array are not obvious: it is not clear that from GetLength(0) and GetLength(1) there is width, and that is height. High risk just to confuse the indices.

4. Using three-dimensional arrays to store color images instead of creating a separate class for the image. In addition to the preceding paragraph, we have to remember which of the indices corresponds to which color component. I also saw how three-dimensional arrays are used to store vectors, both in the form (vx, vy) and in the form (v, angle) . Get confused easily.

5. Using an array instead of a class. Guess what the next function returns?

 public static double[] HoughTransform2(GrayscaleFloatImage image, ref float[][] direction, ColorFloatImage cimage) 

Answer: an array of 11 elements, each of the elements has its own sacred meaning, incomprehensible without a long code analysis. Do not do this! Start a class and name each of the fields humanly.

6. Reuse of variables with changing semantics. grady you see in the code gradx and grady and think that this is a primer of x and y ? But no, this is the module and the angle:

 gradx[x, y] = (float)Math.Sqrt(temp1 * temp1 + temp2 * temp2); grady[x, y] = (float)(Math.Abs(Math.Atan2(temp2, temp1)) * 180 / Math.PI); 

Solution: there should be no magic constants and indexes. Decorate images as separate classes, the pixels themselves should also be typed, and access to the pixels should be carried out only through special methods.

Error 9. The use of some mathematical functions incorrectly or out of place.

Here, the poor understanding of the processor architecture, a set of instructions and the time of their execution is to blame. Forgivably, comes with experience, but some points I will note:

1. Squaring as Math.Pow(x, 2) or pow(x, 2) instead of x * x .
Compilers do not optimize these constructions; instead of one-cycle multiplication, they generate a rather complex code, including the calculation of the exponent and the logarithm, which leads to a decrease in speed by an order of two.

2. Taking the integer part as (int)Math.Floor((float)(j) / k) , with k real and not changing inside the loop.

Here it would be enough to write (int)(j / k) , and even better (int)(j * inv_k) , where float inv_k = 1.0f / k .

The fact is that floor returns a real number, which must then be further converted into an integer. It turns out an extra rather expensive operation. Well, replacing division by multiplication is just optimization, the division operation is still expensive.

3. Calculate the inverse value.

 double _sum = pow(sum, -1); 

Why do so when you can write _sum = 1.0 / sum?

Solution: use math functions only where they are needed.

Error 10. Ignorance of the language

And again problems with math:

1. Confusion with types. Using long long for pixel indices instead of int , constant conversions between float , double and int . For example, why write (float)(1.0 / 16) when you can write 1.0f / 16.0f ?

2. Calculate the polar angle through fussing with atan and the problem of dividing by zero instead of using atan2 , which does exactly what is needed.

3. Unusual exponent and magic constants:

 g=(float)Math.pow(2.71,-(d*d)/(2*sigma*sigma)); t=((float)1/((float)Math.sqrt(6.28)*sigma)); 

Here, the student simply forgot about the existence of the function exp and the constant pi . And instead of (float)1 you can simply write 1.0f .

Solution: program more, the only way you will gain experience.

Error 11. Obfuscation Code

Novice programmers love to show their skills, preferring to write a short code, rather than understandable.

1. Complex cycles

 for (int x1 = x - 1, x2 = 0; x1 <= x + 1; x1++, x2++) { for (int y1 = y - 1, y2 = 0; y1 <= y + 1; y1++, y2++) { 

Here it would be right to make a cycle from -1 to 1, and calculate x1 and x2 already inside the cycle, well, change the order:

 for (int j = -1; j <= 1; j++) { int y1 = y + j, y2 = j + 1; for (int i = -1; i <= 1; i++) { int x1 = x + i, x2 = i + 1; 

It would turn out even faster due to the fact that compilers easily optimize simple cycles.

2. Cool features

 long long ksize = llround(fma(ceil(3 * sigma), 2, 1)), rad = ksize >> 1; 

And normal people just write

 int rad = (int)(3.0f * sigma); int ksize = 2 * rad + 1; 

And this is generally beyond good and evil:

 kernel[idx] = exp(ldexp(-pow(_sigma * (rad - idx), 2), -1)); 

For those who do not understand: ldexp(x, -1) - this is just a division by 2.

Solution: just remember that sooner or later you will beat off your fingers with a hammer for such a code.

Error 12. Corruption of the values ​​of processed images

Here is a piece of code from the non-maximum suppression, which is part of the Canny algorithm:

 for x in xrange(grad.shape[0]): for y in xrange(grad.shape[1]): if ((angle[x, y] == 0) and ((grad[x, y] <= grad[getinds(grad, x + 1, y)]) or (grad[x, y] <= grad[getinds(grad, x - 1, y)]))) or\ ((angle[x, y] == 0.25) and ((grad[x, y] <= grad[getinds(grad, x + 1, y + 1)]) or (grad[x, y] <= grad[getinds(grad, x - 1, y - 1)]))) or\ ((angle[x, y] == 0.5) and ((grad[x, y] <= grad[getinds(grad, x, y + 1)]) or (grad[x, y] <= grad[getinds(grad, x, y - 1)]))) or\ ((angle[x, y] == 0.75) and ((grad[x, y] <= grad[getinds(grad, x + 1, y - 1)]) or (grad[x, y] <= grad[getinds(grad, x - 1, y + 1)]))): grad[x, y] = 0 

Here, some values ​​vanish grad[x, y] = 0 , and on subsequent iterations of the cycles they are addressed. An error would not have occurred if a new image were created to calculate the intermediate result and the current one was not overwritten.

Solution: do not seek to save memory ahead of time, think about the functional paradigm.

The remaining errors

The remaining errors are already non-programmatic. These are errors in the implementation of algorithms due to their misunderstanding, they are individual. For example, the wrong choice of kernel size for a Gaussian filter.

The Gauss filter is one of the main filters in image processing. It underlies a huge number of algorithms: detection of edges (edges) and ridges (ridges), searching for key points, sharpening, etc. The Gauss filter has a “sigma” parameter that determines the level of blur, its core is described by the formula:

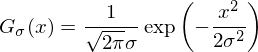
and the schedule has the form:

This function never vanishes, and a bundle with a kernel of infinite size does not make sense. Therefore, the core size is chosen so that the error is negligible. For practical tasks, it is enough to take a kernel with a radius (int)(3 * sigma) - the error will be less than 1/1000 . Selecting a too small core (red function on the graph above) will result in a distortion of the Gauss filter. The use of a fixed-size kernel, for example, 5x5, leads to incorrect results already at sigma = 1.5 .

Outcome: general guidelines for beginners to work with images

1. Do not use system objects Bitmap, HBITMAP and the like.
2. Before using the library for working with images, start by writing bicycles, and only then rush into battle.
3. Use the float type to store pixel values ​​if byte is not enough to store pixel values ​​in terms of both precision and range. And having gained experience, you can use fixed-point arithmetic and achieve maximum efficiency.
4. When converting from float to byte, be aware of rounding errors and overruns of the type.
5. Remember negative values.
6. Traverse image pixels in the correct order.
7. Test the code thoroughly.
8. Do not be afraid to produce entities. The code should be clear.
9. Use math operations wisely.
10. Learn the language.
11. Do not try to show skill.
12. Read image processing tutorials - they write a lot of useful stuff.

To make it easier to write programs, I created projects that already read and write images, create classes for storing images with the lowest possible functionality, and give an example of an operation on images:

→ Visual Studio 2015, C ++
→ Visual Studio 2015, C #

There are no Linux versions - students using Linux usually have no problems with such things.

Well, for a snack - just pictures.

Selecting contours using the Kanni algorithm. At the top left - the input image, the second from the left - the correct result, the rest - erroneous results.

Increase using bicubic interpolation.