Simple computer control with voice

If you are interested in how to help the immobilized person to control the computer to communicate with the outside world - you are here. If you are interested in how chalk-frequency cepstral coefficients and neural networks are related to this, you can also go here.

Part I. Software for computer control with voice

A person asked me to write a program that would allow him to control a computer mouse with his voice. Then I couldn’t imagine that a person who is almost completely paralyzed, who cannot even turn his head, or can only talk, is able to develop violent activities, helping himself and others to live an active life, acquire new knowledge and skills, work and earn money. , to communicate with other people around the world, to participate in the competition of social projects.

Let me bring here a couple of links to websites, the author and / or ideological inspirer of which is this person - Alexander Makarchuk from Borisov, Belarus:
')

	"At the Owl" - a school of distance learning for people with disabilities. sova.by
	"Without restrictions" - tips for those who need to work on a computer without hands bezogranicheniy.ru

To work on a computer, Alexander used the Vocal Joystick program — a design by students of the University of Washington, made with the money of the National Science Foundation (NSF). See melodi.ee.washington.edu/vj


The program was made in 2005-2009 and worked well on Windows XP. In more recent versions of Windows, the program may freeze, which is unacceptable for a person who cannot get out of the chair and restart it. Therefore, the program had to be redone.

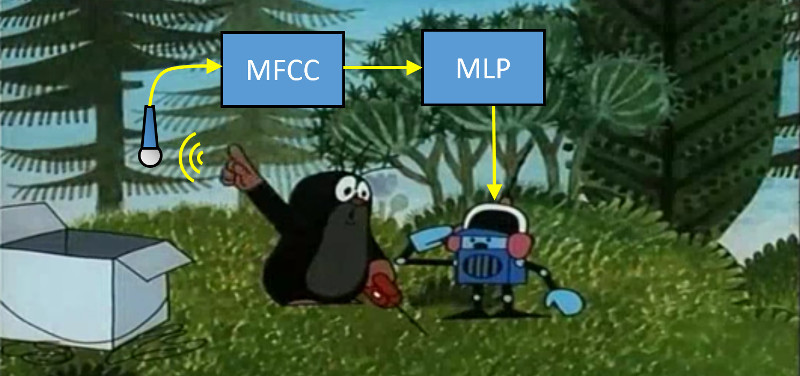
There are no source texts, there are only separate publications that reveal the technologies on which it is based (MFCC, MLP - read about it in the second part).

In the image and likeness of a new program was written (about three months).

Actually, see how it works, you can here :



Download the program and / or view the source code here .

No special actions are needed to install the program, just click on it and launch it. The only thing, in some cases, is required to be running as administrator (for example, when working with the “Comfort Keys Pro” virtual keyboard):



Perhaps it is worth mentioning here about other things that I previously did in order to be able to control the computer without hands.

If you have the ability to turn your head, then a gyroscope attached to the head can be a good alternative to eViacam. You get fast and accurate cursor positioning and independence from lighting.

Read more - here .

If you can only move the pupils of the eyes, then you can use the tracker of the direction of gaze and the program for it (it can be difficult if you wear glasses).

Read more - here .

Part II. How does it work?

From the published materials about the program “Vocal Joystick” it was known that it works as follows:

1. Cutting audio stream into frames of 25 milliseconds with overlaps of 10 milliseconds
2. Obtaining 13 kepstral coefficients (MFCC) for each frame
3. Check that one of the 6 memorized sounds (4 vowels and 2 consonants) is pronounced using a multilayer perceptron (MLP)
4. Embodiment found sounds in motion / mouse clicks

The first task is remarkable only because for its solution in real time it was necessary to introduce three additional streams into the program, since reading data from a microphone, processing sound, playing sound through a sound card occurs asynchronously.

The latter task is simply implemented using the SendInput function.

I think the second and third tasks are of the greatest interest. So.

Task number 2. Getting 13 kepstral coefficients

If someone is not in the subject - the main problem of computer recognition of sounds is the following: it is difficult to compare two sounds, since two sound waves unlike in outline may sound similar in terms of human perception.

And among those who are engaged in speech recognition, there is a search for a “philosopher's stone” - a set of features that would uniquely classify a sound wave.

Of those signs that are available to the general public and described in textbooks, the most widespread are the so-called chalk-frequency cepstral coefficients (MFCC).

Their history is such that they were originally intended for something completely different, namely, to suppress the echo in the signal (the informative article on this topic was written by the distinguished Oppenheim and Shafer, may joy be in the homes of these noble husbands. See AV Oppenheim and RW Schafer, “ From Frequency to Quefrency: A History of the Cepstrum ”).

But the person is designed in such a way that he is inclined to use what is best known to him. And those who dealt with speech signals had the idea to use the ready-made compact signal representation in the form of the MFCC. It turned out that, in general, works. (One of my friends, a specialist in ventilation systems, when I asked him how to make a summerhouse, suggested using ventilation boxes. Just because he knew them better than other building materials).

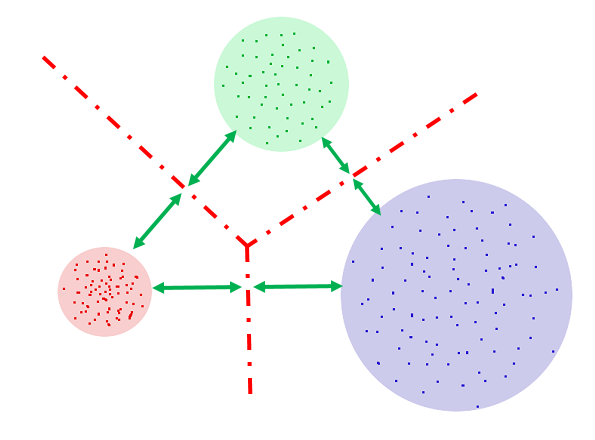
Is MFCC a good classifier for sounds? I would not say. The same sound, pronounced by me into different microphones, falls into different areas of the space of MFCC coefficients, and the ideal classifier would draw them side by side. Therefore, in particular, when changing the microphone, you must re-teach the program.



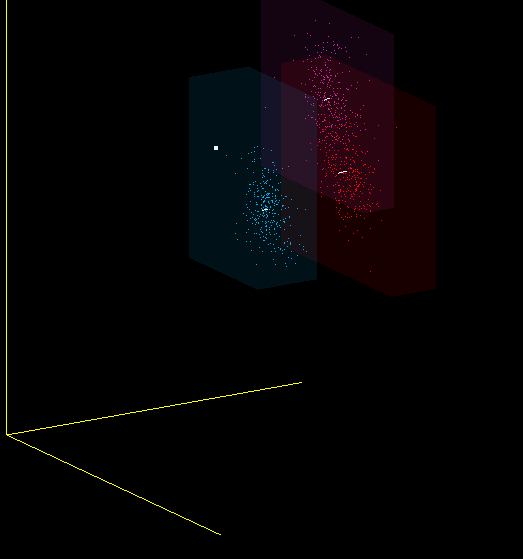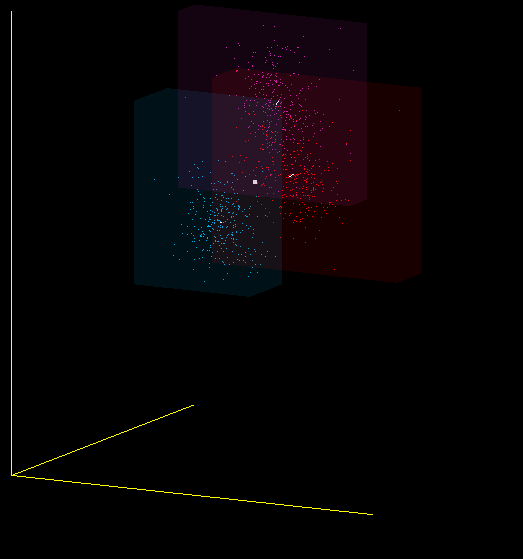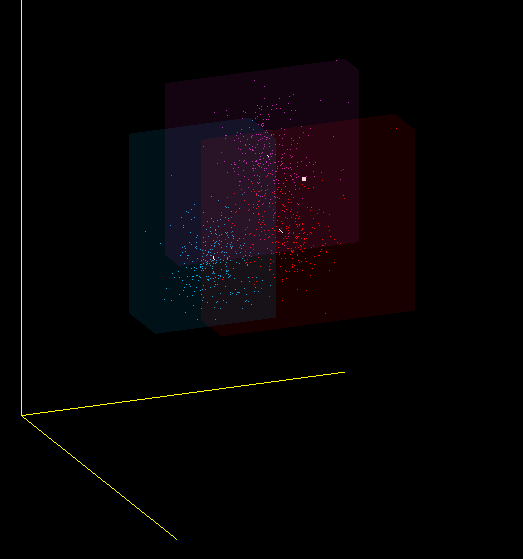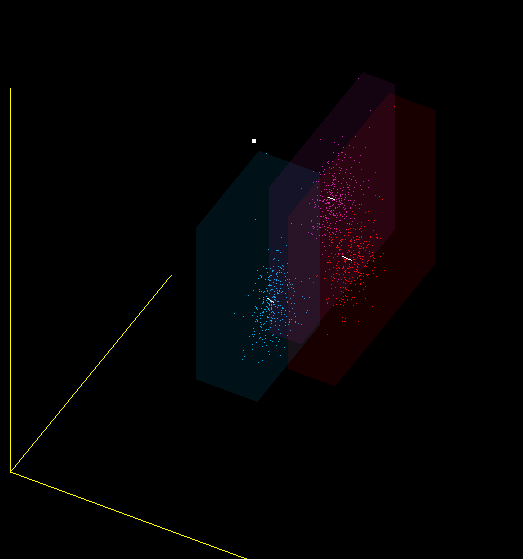
This is just one of the projections of the 13-dimensional MFCC space in 3-dimensional, but it also shows that I mean - red, purple and blue dots are obtained from different microphones: (Plantronix, built-in microphone array, Jabra), but the sound was pronounced alone.

However, since I cannot offer anything better, I will also use the standard method - the calculation of MFCC coefficients.

In order not to be mistaken in the implementation, the first versions of the program used the code from the well-known CMU Sphinx program, more precisely, its implementation in C, called pocketsphinx, developed at Carnegie Mellon University (world with both of them! (C) Hottabych ).

The source codes of pocketsphinx are open, but bad luck - if you use them, you must in your program (both in the source and in the executable module) write the text containing, among other things, the following:

* This work was supported in part by funding from the Defense Advanced * Research Projects Agency and the National Science Foundation of the * United States of America, and the CMU Sphinx Speech Consortium. 

It seemed to me unacceptable, and I had to rewrite the code. This affected the speed of the program (for the better, by the way, although the “readability” of the code suffered a little). Largely due to the use of the “Intel Performance Primitives” libraries, but he himself has also optimized something, like the MEL filter. However, testing on test data showed that the resulting MFCC coefficients are completely analogous to those obtained using, for example, the sphinx_fe utility.

In sphinxbase programs, the calculation of MFCC coefficients is performed in the following steps:

Step	Sphinxbase function	The essence of the operation
one	fe_pre_emphasis	A large part of the previous reference is subtracted from the current reference (for example, 0.97 from its value). Primitive low-pass filter.
2	fe_hamming_window	Hamming window - fading at the beginning and end of the frame
3	fe_fft_real	Fast Fourier Transform
four	fe_spec2magnitude	From the usual spectrum we get the power spectrum, losing the phase
five	fe_mel_spec	We group the frequencies of the spectrum [for example, 256 pieces] into 40 piles using the MEL-scale and weighting factors
6	fe_mel_cep	Take the logarithm and apply the DCT2 transform to the 40 values ​​from the previous step. Leave the first 13 result values. There are several variants of DCT2 (HTK, legacy, classic), differing by a constant into which we divide the obtained coefficients, and a special constant for the zero coefficient. You can choose any option, essentially it does not change.

Functions that allow us to separate the signal from the noise and from silence, such as fe_track_snr, fe_vad_hangover, are still wedged in these steps, but we do not need them and will not be distracted by them.

The following substitutions were made for the steps to obtain the MFCC coefficients:

Step	Sphinxbase function	Rework
one	fe_pre_emphasis	cas_pre_emphasis (via frame [i] - = frame [i - 1] * pre_emphasis_alpha;)
2	fe_hamming_window	for (i = 0; i <MM_SOUND_BUFFER_LEN; i ++) buf_in [i] * = (0.53836-0.46164 * cos (2 * 3.14159 * i / (MM_SOUND_BUFFER_LEN-1)));
3	fe_fft_real	ippsDFTFwd_RToCCS_32f
four	fe_spec2magnitude	for (i = 0; i <= DFT_SIZE / 2; i ++) buf_ipp [i] = buf_ipp [i * 2] * buf_ipp [i * 2] + buf_ipp [i * 2 + 1] * buf_ipp [i * 2 + 1];
five	fe_mel_spec	cas_mel_spec (via pre-calculated table)
6	fe_mel_cep	CS_mel_cep (via logarithm + ippsDCTFwd_32f_I)

What next? We have a vector of 13-dimensional space. How to determine which sound it belongs to?

Task number 3. Check that one of the 6 remembered sounds is pronounced

In the original program “Vocal Joystick”, a multi-layer perceptron (MLP) was used for classification - a neural network without newfangled bells and whistles.

Let's see how justified the use of a neural network is here.

Recall what neurons do in artificial neural networks.

If a neuron has N inputs, then the neuron divides the N-dimensional space in half. Hyperplane cuts backhand. At the same time in one half of the space it works (gives a positive answer), and in the other it does not work.

Let's look at [practically] the easiest option - a neuron with two inputs. Naturally, it will halve the two-dimensional space.

Let the input are the values ​​of X1 and X2, which the neuron multiplies by the weights W1 and W2, and adds the free term C.


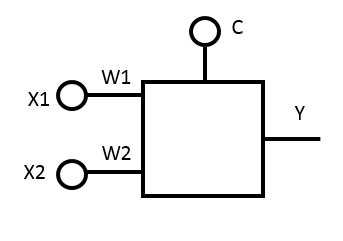
Total, at the output of the neuron (we denote it by Y), we get:

Y = X1 * W1 + X2 * W2 + C

(we will lower while subtleties about sigmoidal functions)

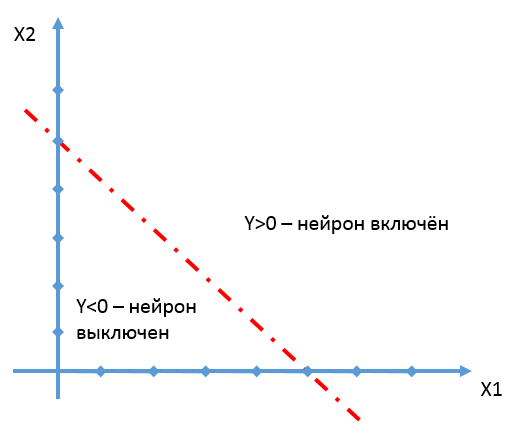
We believe that the neuron is triggered when Y> 0. The straight line given by the equation 0 = X1 * W1 + X2 * W2 + C divides the space into a part, where Y> 0, and a part, where Y <0.

We illustrate what was said with concrete numbers.

Let W1 = 1, W2 = 1, C = -5;



Now let's see how we organize a neural network that would work on a certain area of ​​space, relatively speaking, a spot, and did not work in all other places.

It can be seen from the figure that in order to delineate a region in two-dimensional space, we will need at least 3 straight lines, that is, 3 neurons associated with them.



We will merge these three neurons together using another layer, resulting in a multilayered neural network (MLP).



And if we need the neural network to work in two areas of space, then we will need at least three more neurons (4,5,6 in the figures):


And here we can’t do without the third layer:


And the third layer is almost Deep Learning ...



Now let's turn to another example. Let our neural network should give a positive response at red points, and a negative one at blue points.



If I were asked to cut off straight red from blue, then I would do it something like this:



But a neural network a priori does not know how many direct (neurons) it will need. This parameter must be set before training the network. And the person does it on the basis of ... intuition or trial and error.

If we select too few neurons in the first layer (three, for example), then we can get a cut that will give a lot of errors (the error area is shaded):



But even if the number of neurons is sufficient, as a result of the training, the network can “not converge”, that is, to achieve some stable state, which is far from optimal, when the error rate is high. As it was here, the upper crossbar lay down on two humps and would not leave anywhere. And under it is a large area that generates errors:



Again, the possibility of such cases depends on the initial learning conditions and the sequence of learning, that is, on random factors:

- What do you think will reach that wheel, if it happened, to Moscow or not reach?
- What do you think, will the neural network entangle or not?

There is another unpleasant moment associated with neural networks. Their "forgetfulness."

If you start feeding only the blue dots to the nets, and stop feeding the red ones, then she can easily grab a piece of the red area, moving her borders there:



If neural networks have so many flaws, and a person can draw boundaries much more effectively than a neural network, then why use them at all?

And there is one small, but very significant detail.

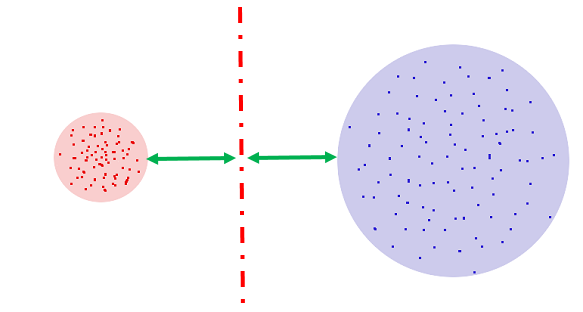
I can very well separate the red heart from the blue background with straight line segments in a two-dimensional space.

I can pretty well separate the statue of Venus from the three-dimensional space surrounding it.

But in four-dimensional space, I can not do anything, sorry. And in the 13-dimensional - all the more.

But for the neural network the dimension of space is not an obstacle. I laughed at her in spaces of small dimension, but it was worth going beyond the ordinary, as she easily made me do.

Nevertheless, the question is still open - how justified is the use of a neural network in this particular task, given the above disadvantages of neural networks.

Let's forget for a second that our MFCC coefficients are in 13-dimensional space, and imagine that they are two-dimensional, that is, points on a plane. How in this case could one sound be separated from another?

Let the MFCC points of sound 1 have a standard deviation of R1, which [roughly] means that points that are not too far from the mean, the most characteristic points, are inside a circle with radius R1. Similarly, the points that we trust in sound 2 are inside a circle with radius R2.



Attention, the question is: where to draw a line that would best separate sound 1 from sound 2?

The answer is: the middle between the boundaries of the circles. Any objections? No objections.
Correction: In the program, this boundary divides the segment connecting the centers of circles in the ratio R1: R2, so it is more correct.



Further, imagine that there are three sounds. In this case, we draw the boundaries between each pair of sounds.



And finally, let's not forget that somewhere in space there is a point, which is a representation of complete silence in the MFCC-space. No, this is not 13 zeros, as it might seem. This is one point that cannot have standard deviation. And the straight lines, with which we will cut it off from our three sounds, can be drawn right along the borders of the circles:



In the figure below, each sound corresponds to a piece of space of its color, and we can always say to which sound one or another point in space belongs (or does not apply to any):



Well, well, now remember that space is 13-dimensional, and what was good at drawing on paper now turns out to be something that does not fit in the human brain.

So, yes, not so. Fortunately, in the space of any dimension, such concepts as point, line, [hyper] plane, [hyper] sphere remain.

We repeat all the same actions in 13-dimensional space: we find the dispersion, determine the radii [hyper] spheres, connect their centers with a straight line, chop it [hyper] with a plane at a point equally distant from the borders [hyper] spheres.

No neural network can more properly separate one sound from another.

Here, however, should make a reservation. All this is true if the information about the sound is a cloud of points deviating from the average equally in all directions, that is, it fits well with the hypersphere. If this cloud were a complex figure, for example, a 13-dimensional curved sausage, then all the above arguments would not be true. And perhaps, with proper training, the neural network could show its strengths here.

But I would not risk it. And would apply, for example, sets of normal distributions (GMM), (which, by the way, is done in CMU Sphinx). It is always more pleasant when you understand which particular algorithm led to the result. And not in the neural network: Oracle, based on its many hours of cooking broth from the data for training, commands you to decide that the requested sound is sound No. 3. (I am especially annoyed when the neural networks are trying to entrust the control of the car. How then in an irregular situation to understand why the car turned left and not right? Almighty Neuron ordered?).

But the sets of normal distributions are a separate large topic that goes beyond the scope of this article.

I hope that the article was useful, and / or your brain meanders squeak.