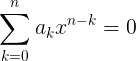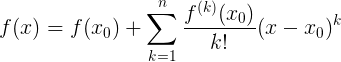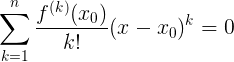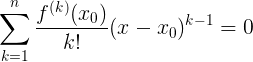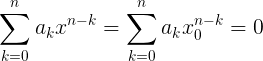Algorithm for finding the equivalent points of the abscissa axis of a polynomial function

Dear habrovchane, welcome! We continue the cycle of pertinent articles, the previous one is located here . Let me remind you that I am only an amateur of mathematics who deals with its moral and aesthetic side, and my ideas may seem uninteresting / useless to you / etc. So:

To begin with, introducing axiomatics into the account of the term "equivalence" in this context will be the right step:
')

• If some coordinate of the x-axis 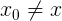from the numerical set satisfies the following condition: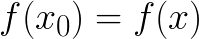
  
  
  
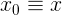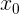  It is believed that (i.e is equivalent to )

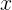Such an axiomatics for the sake of this article, for the sake of convenience, and, strictly speaking, is not entirely correct.

And immediately it would be nice to answer the traditional question: “sorry, but why is this necessary?”. I answer - at least, to search for the remaining roots of the equation of a polynomial (going from equation to function), knowing only one root. As well as a variety of less obvious things. Now we will deal with the resolution of this problem, and then we give the algorithm in general form. For those interested, you are welcome under cat.

Note that we will work on the following class of functions:



For those who do not know what sigma is , it is necessary to clarify that this is equivalent to the following:



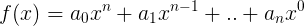
This is nothing more than a general form of a function representing a polynomial. Let's finally create a clear task with a specific example in order to better understand what is happening. So, we have the equation of a third degree polynomial, that is, cubic:



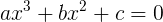
The task: knowing one of the roots of the equation (from any numerical set — be it rational , complex , etc.), find the remaining roots of the equation. And not just to find, but by solving an equation of a lesser degree!

Well, it's time to move from the equation to the function:



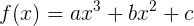
And then, for fun, find all non-zero derivatives of the function:





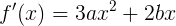
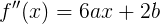
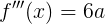
Well, since we’ve found it, let's expand the function in the Taylor series ( where ):



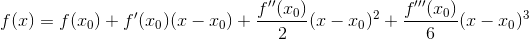
Further recall the above equivalence axioms 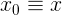for our context:

[by virtue of equality is fair and ]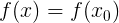

Nothing like? Right! This is the first Taylor expansion term for our function. Then, obviously, for equality to be identical, the other members of the expansion must turn to zero. In other words:



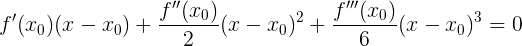
We use the following obvious rule:

• A product is zero if and only if at least one or several factors are zero.

And we can just multiplier 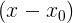to put out of brackets: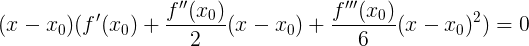



Then:

1. 
   
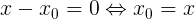
   not suitable , because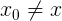 for there will be a tautology of the species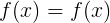
   
   
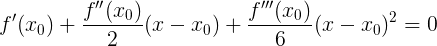
2. 

Here is the second case of applying to the product to zero, it is quite suitable for us! Let's substitute the derivatives:



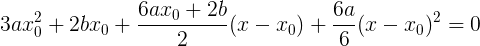
Let's reduce a bit:



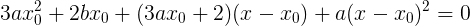
And lo and behold! The equation is second degree (quadratic), while the original equation was cubic ( third degree).

Solving it relatively 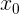we get the following roots: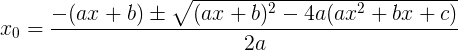



Obviously, the following for our function follows from this:



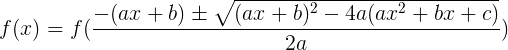
What does this give us for our equation? And the fact that knowing one of the roots of the equation, we will be able to find the other two (and for quadratic complexity).

Corollary : knowing one of the roots of the degree equation , you can lower the degree of the equation to 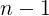, and the root can be from any standard numeric set.

Let's look at a more specific example:



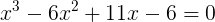
I know that from the roots of the desired equation is 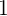. And if we present the equation as a cubic function (according to the algorithm described above), we get the following: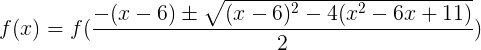



The graph is as follows:


Then for our root :



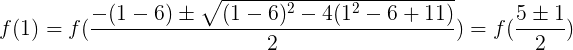
I.e:



Thus, we found the remaining two roots of the cubic equation by solving a quadratic equation. In well-known circles there is a method of dividing by a corner , which also makes it possible to lower the degree. But it works only with integer coefficients (that is, rational ones will have to be reduced to integers, but complex ones are not possible at all).

Also interesting is the fact that from a similar formula of "equivalence" follow the conditions of (non) monotonicity for the nth degree polynomial. You can form it like this:

When found in a polynomial even radical (Where - any radical expression) you can form the following property:

If at any inequality holds , the graph of the desired function is monotonous on the whole set . The reverse is also true if .

Why is that? Yes, because if it is not satisfied, then we simply simply will not be able to calculate 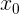because of the tdz of the radicand.

Perhaps it is time to form a general algorithm for finding the equivalent points of the abscissa axis of the polynomial function.

We have an equation in the form of a polynomial of arbitrary degree of general form:



Let's move from the equation to the function:



We expand the function in a Taylor series, where :



We need to find , Consequently:



Then:

1. 
   
   not suitable , because for there will be a tautology of the species
   
   
2. 

Solve the equation for (the degree of which is less than the original ), the roots of which will be equivalence .

Now, in particular, the following is true:

1. 
2. 

Equivalent points found .

Also, do not forget about the condition (not) of monotony and other various consequences of the desired algorithm. It is also worth noting that usually the conditions of monotony are determined by the DHS radical of the roots of the equation 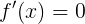. Let me remind you that this way you can search not only for the “other roots”, but also for any 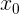such that: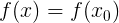



It is also worth mentioning that, according to the Abel – Ruffini theorem , the algorithm will work only up to a general polynomial of degree 5 inclusive (since the roots of a higher order equation more than a fourth cannot be represented as rational functions (i.e., I mean, etc. ).

We fulfilled the task set on Sunday, for this I deviate.

Thanks for attention!