Saltan Spectroscope: laplacians for fan
Christmas days - time to postpone the usual things and remember the fun - kaleidoscopes, mosaics, snowflakes ... Who will draw the most beautiful star?

Symmetry is pleasing to the eye. Mathematics helps the beauty, the Python language and its libraries are mathematical numpy and graphic matplotlib .
KDPV is obtained by visualizing the values of the eigenvectors of a certain symmetric matrix.
The basis is the spectra of regular gratings. Some of their properties have already been considered previously . Here the formulas will work on aesthetics.
So, let's say there is a certain basic set of points located on a plane. There are few requirements - the configuration should be centrally symmetric. For example, a hexagonal grid would be a good choice:
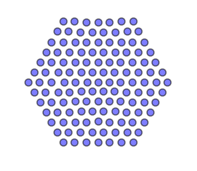
Already beautiful, only somewhat monotonous.
Circles are points. Each is characterized by two coordinates. For a given set of points, you can calculate their own coordinates based on a matrix of squares of distances between points. This is explained in the article mentioned above. To calculate the spectrum, it is necessary to convert the matrix of squares of distances into the Laplacian (which in this case is the correlation matrix) and calculate the spectrum of this Laplacian, that is, to find its own numbers and the corresponding vectors.
')
If we calculate the spectrum for a set of points located on a plane, then there will be only two components in the spectrum - one corresponding to the x coordinate, and the other to y.
And it is necessary to make so that the spectrum "rang", but at the same time retains symmetry. To achieve this is not difficult. It is enough to change (or perturb) the function of the distance between points. For example, you can assume that the distance between points is not equal to the square of the distance, but to its cube, or the inverse distance - you can use any function depending on the distance.
For such a “distance matrix,” the spectrum can no longer be two-dimensional. The algorithm for the decomposition of the distance matrix into the spectrum must somehow select for each point a set of coordinates in order to satisfy the non-standard distance. Such a spectrum starts to ring, - the number of its components in the general case is equal to the total number of points (although zero can be excluded).
If the set of points has symmetry, then part of the components will be degenerate. This means that the same eigenvalue value will correspond to different eigenvectors. In our case, the initial configuration of points is two-dimensional, respectively, and the degree of degeneration will be a multiple of two (probably, there is some kind of theorem for this statement). And this means that such doubly degenerate levels — projections — can be drawn on the plane. In the simplest version - also points.
Assume that the distance function has the following form:
f (R2) = w * Rd + 1 / Rd , where w = dist / n ^ 2, Rd = R2 ^ degree .
Here, dist and degree are two variable disturbance parameters. Then the first 9 degenerate levels for the above basic configuration (hexagonal lattice of size 7) with disturbance parameters dist = -2 , degree = 1 are:

In the upper left corner is the initial configuration. The values of the parameters are chosen in such a way that it is almost not distorted.
All patterns are guaranteed to be different - this follows from the properties of the eigenvectors (although sometimes they are not distinguishable by eye). Some seem more unusual than others. Here, for example, is one of the fancy configurations:

You can take as the source set a square lattice. Then the symmetry will be square:

Since symmetry is reduced, the number of non-degenerate spectra here is twice as large as the degenerate.
If you give the points color and size, then the snowflakes (patterns) will become more fun and diverse. The point is that the color and size of the points can also be formed on the basis of the eigenvectors of this set.
Algorithm of color formation is simple. We use a certain color map (from the available sets in matplotlib ), which converts the value of a point to color, and the very value of a point is taken from some non-degenerate eigenvector. The same for point size. Then you can get about this fun lace:
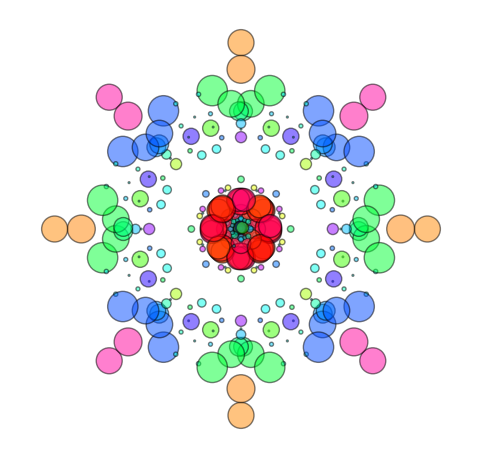
If you vary only the color, then you can play in the children's mosaic:

This mathematics has painted the basic configuration of points in different colors.
If close points are connected by lines, then we get something like a web. According to scientific such an operation is called triangulation . The advantage of the matplotlib package is that there such an operation is available out of the box. The cobwebs are beautiful:

You can delete part of the mask- based triangles:

Triangulation becomes colored if the triangles are filled with different colors:

The choice of color map and color vector strongly influences the perception of the same configuration:

The use of masks sharpens the contours of the patterns:

The number of combinations and variations is almost infinite, the game of patterns is very fancy.
It is possible that the most sophisticated are patterns obtained by drawing contours based on triangulation. These patterns are obtained using the matplotlib tricontour () method. Even the most inconspicuous and boring sets of points acquire completely unexpected variations.

Symmetry can be any, for example, of the 5th order:

Some kind of magic.
All the above patterns were created using the program " Spectroscope " written in Python. The program code is not perfect, but is available .
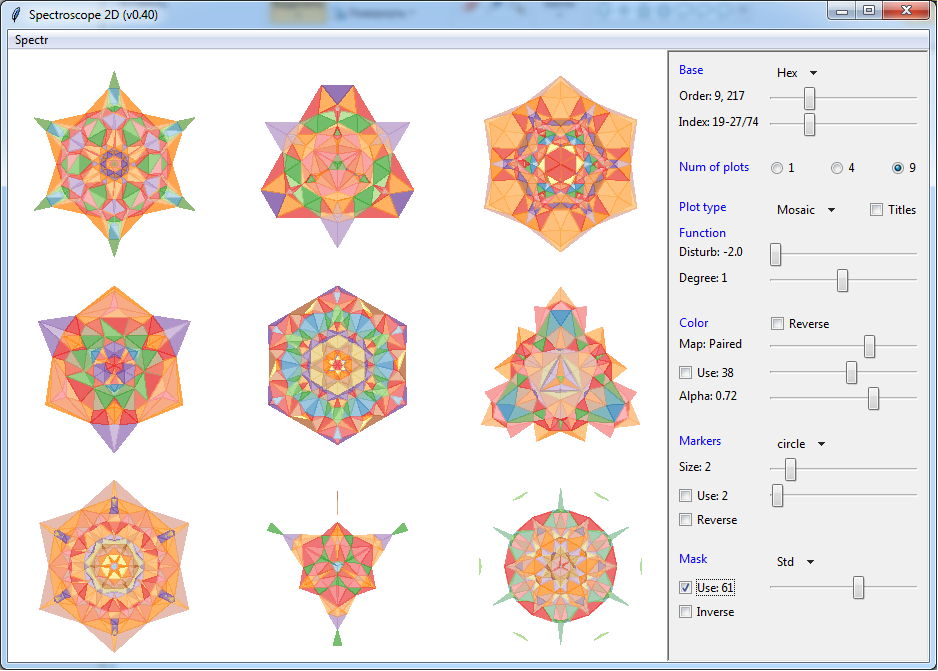
With it, anyone can create patterns, varying parameters through a simple interface.
At the top of the control panel, you can select one of the basic sets of distribution points ( Base ). The base distribution always has an index of one, if the perturbation parameters are -2 ( Disturb ) and 1 ( Degree ), respectively, so you can always look at it.
The most powerful are the basic Hex (hex) and Square (square) sets, since they have the most points. Therefore, they give more varied patterns. But the x-border sets (polygons) and especially Circle (circumference) on the contrary - are emasculated and more interesting for research purposes.
For a basic set, you can specify its size ( Order ) using the slider (slider). The next field ( Index ) sets the number of displayed spectra (levels) available for this set. In this version, you can display 1, 4 or 9 patterns simultaneously.
An important parameter is the pattern type ( Plot type ). It is he who sets the way (mode) to display our eigenvectors. Available are listed above ( Points, Web, Mosaic, Contour ).
The flag " Titles " displays its numerical parameters, the sequence number in the total composition of the levels and the value of the eigenvalue of this level above each spectrum. This is for those who are interested not only in graphics.
Below are two sliders for variation parameters. When they change the spectra come to life. Recall that the right mouse button on the slider - shifts it to the current position, the left - increments.
Then follow the parameters that affect the appearance of the spectra - color, markers and mask. Not in all display modes they are involved. Markers, for example, matter only for the “point” mode, and masks - on the contrary, - for everyone except the point mode.
Perhaps the most important color (Color). To set it, you must specify a color map (Map). But they play with color using a vector (slider with flag Use). The color vector (and the size of the markers too) is chosen, as already noted, from non-degenerate levels.
In the program menu, standard functions are available for saving spectra to files and exporting as images.
There are many areas where you can develop a spectroscope. In addition to the obvious improvements in the interface, development of capabilities (animation, for example, or web access), you need to try to build three-dimensional patterns. They can not only look, but also sculpt).
During games with spectra, several interesting questions of varying degrees of importance arise.
Maybe this is not the most important question, but perhaps the simplest. Obviously, the proportion of degenerate spectra depends on the basic distribution of points. For the basic lattices (hexagonal and square) there are explicit formulas.
For a hexagonal lattice, the number of "snowflakes" Ns is related to the total number of points (nodes) N as:
Ns = (N-1) / 3
In turn, the number of points quadratically depends on the size of the lattice a :
N (a) = 3a (a-1) + 1 . Hence, Ns (a) = a (a-1).
In a square lattice, the number of degenerate spectra is related to the number of points in a similar way:
Ns = N / 4 = a ^ 2/4
How to get such formulas for arbitrary configurations is not very clear. It is possible that the general algorithm does not exist.
Perhaps the most interesting question. The main way to identify spectrum levels is the eigenvalue value. If you sort the data numbers in ascending order, then you can assign an index to each level (the value of its own number). This index seems to identify the spectrum.
In fact, this is not a very reliable way. When the disturbance parameters are varied, the spectra come to life - the patterns begin to breathe (you can see, for example, how the basic distribution “stomps” as the Disturb parameter changes), and their eigenvalues also change. In this case, situations arise when the eigenvalues of different levels approach each other and pass on. That is, the spectra are interchanged. In this case, by the nature of the pattern of the spectrum, you can see where the spectrum is. This “character” must be hashed to a spectrum identifier in some way.
The phenomenon of rapid change in patterns occurs in a narrow band of the perturbation parameter. It looks like something on the phase transition. It is possible that this is a known phenomenon. In a phase transition, both the type of spectra and their relative location change. The program selected the type of perturbed function such that when the Disturbance parameter Disturb is changed, the function changes sign. It can be seen that when the parameter changes from the minimum to the maximum, the basic distribution moves from the first index to the last. This transition seems to be carried out by moving the base pattern in indices from the smallest to the largest. After some time, the modified base pattern appears on the last index. Which then evolves to the original base configuration.
However, in large configurations, it seems, no one moves anywhere (well, or it is impossible to track). It is just that at a certain moment a rudiment of a new basic configuration appears in the right place (at the maximum index). In short, who cares - look).
If there was any parameter to identify one’s own levels, one could more accurately track the movement (or death and birth?) Of the spectra. And to show on the picture always given spectra regardless of the values of their own numbers.
also not very successful. Patterns periodically rotate right / left. It is not clear how the easiest way to always orient them in one direction.
When the base configuration is a simple circle (points at the vertices of regular polygons), the phenomenon of divisors of integers occurs. In this configuration, all points are equal. Accordingly, all the degenerate levels (and there are no others here) are also coordinates of the vertices of the polygons (lie on the circle). But at the same time, the spectra of simple polygons (the number of vertices is a prime number) differ from the composite ones. In the spectra of simple all levels are also simple polygons with the same number of vertices. And in the spectra of the composite levels consist of divisors of the vertices of the base polygon.
For example, the spectrum of a 30-gon consists of 14 degenerate levels (projections). Of these, four 30-gons, four 15-gons, two 10-gons, one 6-gon, two 5-gons and one 3-gon. Why exactly such a distribution of levels by divisors is not clear (but strongly and did not penetrate). Perhaps this has already been explained somewhere in group theory.
That's all for now. Good luck in your creative search and Merry Christmas!

Symmetry is pleasing to the eye. Mathematics helps the beauty, the Python language and its libraries are mathematical numpy and graphic matplotlib .
Spectra of impossible gratings
KDPV is obtained by visualizing the values of the eigenvectors of a certain symmetric matrix.
The basis is the spectra of regular gratings. Some of their properties have already been considered previously . Here the formulas will work on aesthetics.
So, let's say there is a certain basic set of points located on a plane. There are few requirements - the configuration should be centrally symmetric. For example, a hexagonal grid would be a good choice:

Already beautiful, only somewhat monotonous.
Circles are points. Each is characterized by two coordinates. For a given set of points, you can calculate their own coordinates based on a matrix of squares of distances between points. This is explained in the article mentioned above. To calculate the spectrum, it is necessary to convert the matrix of squares of distances into the Laplacian (which in this case is the correlation matrix) and calculate the spectrum of this Laplacian, that is, to find its own numbers and the corresponding vectors.
')
If we calculate the spectrum for a set of points located on a plane, then there will be only two components in the spectrum - one corresponding to the x coordinate, and the other to y.
And it is necessary to make so that the spectrum "rang", but at the same time retains symmetry. To achieve this is not difficult. It is enough to change (or perturb) the function of the distance between points. For example, you can assume that the distance between points is not equal to the square of the distance, but to its cube, or the inverse distance - you can use any function depending on the distance.
For such a “distance matrix,” the spectrum can no longer be two-dimensional. The algorithm for the decomposition of the distance matrix into the spectrum must somehow select for each point a set of coordinates in order to satisfy the non-standard distance. Such a spectrum starts to ring, - the number of its components in the general case is equal to the total number of points (although zero can be excluded).
If the set of points has symmetry, then part of the components will be degenerate. This means that the same eigenvalue value will correspond to different eigenvectors. In our case, the initial configuration of points is two-dimensional, respectively, and the degree of degeneration will be a multiple of two (probably, there is some kind of theorem for this statement). And this means that such doubly degenerate levels — projections — can be drawn on the plane. In the simplest version - also points.
Assume that the distance function has the following form:
f (R2) = w * Rd + 1 / Rd , where w = dist / n ^ 2, Rd = R2 ^ degree .
Here, dist and degree are two variable disturbance parameters. Then the first 9 degenerate levels for the above basic configuration (hexagonal lattice of size 7) with disturbance parameters dist = -2 , degree = 1 are:

In the upper left corner is the initial configuration. The values of the parameters are chosen in such a way that it is almost not distorted.
All patterns are guaranteed to be different - this follows from the properties of the eigenvectors (although sometimes they are not distinguishable by eye). Some seem more unusual than others. Here, for example, is one of the fancy configurations:

You can take as the source set a square lattice. Then the symmetry will be square:

Since symmetry is reduced, the number of non-degenerate spectra here is twice as large as the degenerate.
Add color and size
If you give the points color and size, then the snowflakes (patterns) will become more fun and diverse. The point is that the color and size of the points can also be formed on the basis of the eigenvectors of this set.
Algorithm of color formation is simple. We use a certain color map (from the available sets in matplotlib ), which converts the value of a point to color, and the very value of a point is taken from some non-degenerate eigenvector. The same for point size. Then you can get about this fun lace:

If you vary only the color, then you can play in the children's mosaic:

This mathematics has painted the basic configuration of points in different colors.
Spider webs
If close points are connected by lines, then we get something like a web. According to scientific such an operation is called triangulation . The advantage of the matplotlib package is that there such an operation is available out of the box. The cobwebs are beautiful:

You can delete part of the mask- based triangles:

Mosaics
Triangulation becomes colored if the triangles are filled with different colors:

The choice of color map and color vector strongly influences the perception of the same configuration:

The use of masks sharpens the contours of the patterns:

The number of combinations and variations is almost infinite, the game of patterns is very fancy.
Contours
It is possible that the most sophisticated are patterns obtained by drawing contours based on triangulation. These patterns are obtained using the matplotlib tricontour () method. Even the most inconspicuous and boring sets of points acquire completely unexpected variations.

Symmetry can be any, for example, of the 5th order:

Some kind of magic.
Spectroscope
All the above patterns were created using the program " Spectroscope " written in Python. The program code is not perfect, but is available .

With it, anyone can create patterns, varying parameters through a simple interface.
At the top of the control panel, you can select one of the basic sets of distribution points ( Base ). The base distribution always has an index of one, if the perturbation parameters are -2 ( Disturb ) and 1 ( Degree ), respectively, so you can always look at it.
The most powerful are the basic Hex (hex) and Square (square) sets, since they have the most points. Therefore, they give more varied patterns. But the x-border sets (polygons) and especially Circle (circumference) on the contrary - are emasculated and more interesting for research purposes.
For a basic set, you can specify its size ( Order ) using the slider (slider). The next field ( Index ) sets the number of displayed spectra (levels) available for this set. In this version, you can display 1, 4 or 9 patterns simultaneously.
An important parameter is the pattern type ( Plot type ). It is he who sets the way (mode) to display our eigenvectors. Available are listed above ( Points, Web, Mosaic, Contour ).
The flag " Titles " displays its numerical parameters, the sequence number in the total composition of the levels and the value of the eigenvalue of this level above each spectrum. This is for those who are interested not only in graphics.
Below are two sliders for variation parameters. When they change the spectra come to life. Recall that the right mouse button on the slider - shifts it to the current position, the left - increments.
Then follow the parameters that affect the appearance of the spectra - color, markers and mask. Not in all display modes they are involved. Markers, for example, matter only for the “point” mode, and masks - on the contrary, - for everyone except the point mode.
Perhaps the most important color (Color). To set it, you must specify a color map (Map). But they play with color using a vector (slider with flag Use). The color vector (and the size of the markers too) is chosen, as already noted, from non-degenerate levels.
In the program menu, standard functions are available for saving spectra to files and exporting as images.
There are many areas where you can develop a spectroscope. In addition to the obvious improvements in the interface, development of capabilities (animation, for example, or web access), you need to try to build three-dimensional patterns. They can not only look, but also sculpt).
Mathematical Aspects
During games with spectra, several interesting questions of varying degrees of importance arise.
Calculation of the number of degenerate spectra
Maybe this is not the most important question, but perhaps the simplest. Obviously, the proportion of degenerate spectra depends on the basic distribution of points. For the basic lattices (hexagonal and square) there are explicit formulas.
For a hexagonal lattice, the number of "snowflakes" Ns is related to the total number of points (nodes) N as:
Ns = (N-1) / 3
In turn, the number of points quadratically depends on the size of the lattice a :
N (a) = 3a (a-1) + 1 . Hence, Ns (a) = a (a-1).
In a square lattice, the number of degenerate spectra is related to the number of points in a similar way:
Ns = N / 4 = a ^ 2/4
How to get such formulas for arbitrary configurations is not very clear. It is possible that the general algorithm does not exist.
Spectrum Level Identification
Perhaps the most interesting question. The main way to identify spectrum levels is the eigenvalue value. If you sort the data numbers in ascending order, then you can assign an index to each level (the value of its own number). This index seems to identify the spectrum.
In fact, this is not a very reliable way. When the disturbance parameters are varied, the spectra come to life - the patterns begin to breathe (you can see, for example, how the basic distribution “stomps” as the Disturb parameter changes), and their eigenvalues also change. In this case, situations arise when the eigenvalues of different levels approach each other and pass on. That is, the spectra are interchanged. In this case, by the nature of the pattern of the spectrum, you can see where the spectrum is. This “character” must be hashed to a spectrum identifier in some way.
Phase transitions
The phenomenon of rapid change in patterns occurs in a narrow band of the perturbation parameter. It looks like something on the phase transition. It is possible that this is a known phenomenon. In a phase transition, both the type of spectra and their relative location change. The program selected the type of perturbed function such that when the Disturbance parameter Disturb is changed, the function changes sign. It can be seen that when the parameter changes from the minimum to the maximum, the basic distribution moves from the first index to the last. This transition seems to be carried out by moving the base pattern in indices from the smallest to the largest. After some time, the modified base pattern appears on the last index. Which then evolves to the original base configuration.
However, in large configurations, it seems, no one moves anywhere (well, or it is impossible to track). It is just that at a certain moment a rudiment of a new basic configuration appears in the right place (at the maximum index). In short, who cares - look).
If there was any parameter to identify one’s own levels, one could more accurately track the movement (or death and birth?) Of the spectra. And to show on the picture always given spectra regardless of the values of their own numbers.
Picture stabilization
also not very successful. Patterns periodically rotate right / left. It is not clear how the easiest way to always orient them in one direction.
Dividers
When the base configuration is a simple circle (points at the vertices of regular polygons), the phenomenon of divisors of integers occurs. In this configuration, all points are equal. Accordingly, all the degenerate levels (and there are no others here) are also coordinates of the vertices of the polygons (lie on the circle). But at the same time, the spectra of simple polygons (the number of vertices is a prime number) differ from the composite ones. In the spectra of simple all levels are also simple polygons with the same number of vertices. And in the spectra of the composite levels consist of divisors of the vertices of the base polygon.
For example, the spectrum of a 30-gon consists of 14 degenerate levels (projections). Of these, four 30-gons, four 15-gons, two 10-gons, one 6-gon, two 5-gons and one 3-gon. Why exactly such a distribution of levels by divisors is not clear (but strongly and did not penetrate). Perhaps this has already been explained somewhere in group theory.
That's all for now. Good luck in your creative search and Merry Christmas!
Source: https://habr.com/ru/post/319060/
All Articles