Galois field on Scala

Introduction

This article will discuss the topic of building and working with finite fields (or Galois fields), which are used in cryptography, information theory and coding, and other sciences, ie have a wide practical application. A dry theory about groups / rings / fields can be found at Paul Galois , and there will be more practice and implementation in the Scala language.

Types and limitations

First, we should discuss the technical problems associated with the representation of polynomials in memory, taking into account the size of the type Int in the Scala language. Requirements are listed below.

• Int type in Scala / Java has a size of 32 bits
• You can use bits: 0..30 - 31, since the 32nd bit is a sign
• Polynomials must be represented by numbers in the range 0..29.
• Irreducible polynomials (or modules) have a range of 1..30
• The final field has 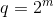items

Implementation

We first describe the Polynomial class, which implements a polynomial and 4 operations. This type of polynomial is a “semi-finished product” and is not tied to a finite field.

class Polynomial(_p: Int) { val polynomial: Int = _p def order: Int = = { ... } def mul(p: Polynomial): Polynomial = { ... } def div(p: Polynomial): (Int, Int) = { ... } def add(p: Polynomial): Polynomial = { ... } def sub(p: Polynomial): Polynomial = { ... } override def toString: String = Integer.toBinaryString(this.polynomial) } 

Next, the FiniteField abstract class, which will be the parent of the Galois fields. Inside FiniteField contains the internal class FiniteFieldPolynomial , this structure allows you to ensure safety during operations.
')
Security is that operations can be performed only with polynomials from one field.

Pay attention to the modulo term; this is a module (or an irreducible polynomial) power of a field.

 abstract class FiniteField(_initBitNumber: Int) { type T = Polynomial type GFPolynomial <: FiniteFieldPolynomial protected val checkBitNumber: Int => Int = ??? val modulo: T val bits: Int = checkBitNumber(_initBitNumber) protected def createModulo(): Option[Int] def createPolynomial(_initPolynomial: Int): FiniteFieldPolynomial abstract class FiniteFieldPolynomial { protected val p: T def +(other: GFPolynomial): GFPolynomial def -(other: GFPolynomial): GFPolynomial = { this + other } def *(other: GFPolynomial): GFPolynomial def /(other: GFPolynomial): GFPolynomial = this * other.mulInverse def addInverse: GFPolynomial = self def mulInverse: GFPolynomial def self: GFPolynomial } } 

An important step in constructing a Galois field is the calculation of the irreducible polynomials of the degree of the field, as well as the choice of one of them. The mathematics of this process can be found under the link Irreducible polynomials .

An irreducible polynomial will be used for multiplication and division operations, just like a prime number for a number field. .

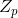In other words, irreducible polynomials play the same role in sets of polynomials as primes in sets of integers.

Simplified code for finding the set of irreducible polynomials is presented below. The algorithm is as follows:

1. if the required order deg is 1, then simply return a ready list of irreducible polynomials of degree 1
2. in the case when the required order is more than 1:
   
   1. generate all polynomials of order deg (let P be the set of these polynomials)
   2. find a list of irreducible polynomials of degree 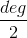(let G be the set of these irreducible polynomials)
      
   3. if polynomial 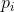divisible by no polynomial 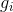, then it is irreducible, it means you need to add 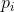to the resulting list of polynomials-modules
   
   

    object IrreduciblePolynomials{ private def check(p: Int, list: List[Int]): Boolean = { val pol = Polynomial(p) list.foreach((item: Int) => { val i = Polynomial(item) if ((pol div i)._2 == 0){ return false } }) true } def calcIrreducible(_deg: Int): List[Int] = { def calc(deg: Int): List[Int] = { if (deg == 1) return List[Int](2, 3) // d > 2 var resultList = ListBuffer[Int]() // generate all polynomials of degree d val n = 1 << deg val nd = if (_deg.equals(deg)) deg >> 1 else deg - 1 val list: List[Int] = calc(nd) for(i <- 0 until n){ val t = i ^ n // polynomial of P set, for testing if (check(t, list)) resultList += t } resultList.toList ::: list } if (_deg < 1) return Nil calc(_deg).filter(_ >= (1 << _deg)) } } 

   
   It remains to implement a specific class-successor FiniteField , which will be a finished final field.
   
   

    class GaloisField(_initBitNumber: Int = FiniteField.DEFAULT_BIT_NUMBER) extends FiniteField(_initBitNumber) { override val modulo: Polynomial = ... protected def createModulo(): Option[Int] = { val list = IrreduciblePolynomials(this.bits) list.headOption } def createPolynomial(_initPolynomial: Int): GFPolynomial = { ... } def createPolynomial(_binInitPolynomial: String): GFPolynomial = { ... } class GFPolynomial private[GaloisField](_p: Int, _m: Int) extends FiniteFieldPolynomial with Comparable[GFPolynomial]{ override def equals(other: Any): Boolean = other match { case other: GFPolynomial => this.p.polynomial == other.p.polynomial case _ => false } override protected val p = Polynomial(_p) def this(other: GFPolynomial){ this(other.p.polynomial, bits) } override def self: GFPolynomial = this override def +(other: GFPolynomial): GFPolynomial = { GFPolynomial(this.p.polynomial ^ other.p.polynomial, bits) } override def -(other: GFPolynomial): GFPolynomial = { // In this case add and subtract are the same this + other } override def *(other: GFPolynomial): GFPolynomial = { val result: Polynomial = this.p mul other.p if (result.order >= bits){ GFPolynomial((result div modulo)._2, bits) } else GFPolynomial(result.polynomial, bits) } override def mulInverse: GFPolynomial = { if (p.polynomial == 0) throw new NoSuchElementException("Error: there is no multiplicative inverse for zero") var r1: Polynomial = Polynomial(modulo.polynomial) var r2: Polynomial = this.p var s1 = Polynomial(1) var s2 = Polynomial(0) var t1 = Polynomial(0) var t2 = Polynomial(1) var t = Polynomial(0) var s = Polynomial(0) var r = Polynomial(0) while(r2.polynomial > 0){ val q: Polynomial = Polynomial((r1 div r2)._1) r = r1 sub (q mul r2) r1 = r2; r2 = r s = s1 sub (q mul s2); s1 = s2; s2 = s t = t1 sub (q mul t2); t1 = t2; t2 = t } GFPolynomial(t1.polynomial, bits) } } } 

   
   The result of multiplication can "get out" beyond the field, so sometimes it is necessary to divide the result by the module of the field. Notice how division is implemented, it is the multiplication of a by the multiplicative inversion of b .
   
   In turn, the inversion is found using the division defined in the Polynomial class.
   
   

   Conclusion

   
   The result was a homemade implementation of Galois fields, which can be further improved by increasing the possible size of the field (instead of Int, use long arithmetic or something like that).
   
   This article may be useful to students and to all who are interested in the topic of abstract algebra, fields, and coding theory.
   
   The complete application code can be found on github .