After not much persuasion, I was convinced that the 30th place is not so bad, and it’s worth writing an article. I am a member with the nickname Stef , and took about 30 places in the sandbox.

The picture painted nearby has a deep meaning - instead of taking enough time and being a competition winner, I went the other way - I spent one third of the time on what was not necessary to do. To be more precise, I took up the path finding algorithm in space, where there are no impenetrable walls, but there are only trees that can either be chopped or walked next to them.

What came out of this, you can see in the video , and if you want to know all the secrets of the forest, please ask under cat.

First I will tell you a little about the competition itself. This year the competition rules were based on the popular computer genre MOBA . The basic concepts of this genre were preserved - the appearance of creeps on 3 lines near the bases; river with runes; 5 heroes on each side.
')
But despite this, there was no full-fledged MOBA - it was not enough to move from line to line, to defend the base in fact, too, and the development was only in the form of pumping skills from a given limited set. The finale among the tops came down to the fact that the game was played according to the principle: “the one who quickly demolishes the enemy’s base on the center line won the game”, and it was demolished in a blast, from 4 to 6 waves of creeps.

As a person familiar with this genre not by hearsay, at the very beginning of the competition I became suspicious and suggested that there would be such a tactic in the finale - all in the middle. Unfortunately, the balance has not changed for the better, and I decided to play my game, not the one that will lead to victory.

Architecture

This year I wrote a strategy in C ++, which I thought was closer to me. I regretted this decision - I didn’t have enough opportunities from high-level languages, I got used to them. By the end, my program included 141 .h or .cpp files. It looked like this: architecture forests .

From this picture you can see the main idea of ​​architecture:

• General-purpose layer - It includes such folders as: Algorithms, Common, Environment. The location of classes between these folders is not entirely correct, especially between the Algorithms folder and the Environment.
• The command layer is a set of classes that implements one of three protocols: MoveCommand, AttackCommand, CastCommand. They were responsible for the logic: where to go, who to attack, what to cast.
• Layer tactics - This includes folders Strategy, Tactics, Role:
  
  
  • Strategy is an adder of team results and contains a basic set to simplify working with teams.
  • Role - the base classes defining the behavior of the magician - just a set of numbers.
  • Tactics - Describes the strategy and roles for this strategy. Under each round, they are different. And there are several of them for the final.

The architecture turned out to be quite large and redundant, especially the command layer. What led to some time consuming.

Time

Before the start of the competition, I set up a program for counting time (toggl), and used it constantly. I will immediately answer one question of interest to many - how much time and energy is spent on the Olympiad? - Yes many. It is very difficult to combine it with work and family, and in fact it is necessary to sacrifice sleep for the sake of it. Students in this regard are simpler, but I think it is also not easy.

Time spent weekly:

• First - 26 hours
• Second - 26 hours
• Third - 27 hours
• Fourth - 34.5 hours
• Fifth - 38.5 hours
• Sixth (before the final) - 10 hours
• After the final - 15 hours

Total: 177 hours.

In the second round, I took 103rd place, despite the fact that the sandbox was high in the ranking, and I wanted to get to the Final through the sandbox, but I could not. Before the final, I was at the 80-90 place with the understanding that I was already tired and I can not continue to write at night, for this reason I gave up writing the Olympiad for a week, well, and as a result, I did not make it to the final.

After some rest and the end of the finals, I spent about 17 hours on fixing bugs and small improvements of the strategy, which helped me to rise from 80-90 places to 20-30. At this point, I finally realized that writing the Olympics at night was a bad idea - almost all the code improvements consisted of typo edits, which in turn appeared due to carelessness, which suffered greatly at night.

Time spent on tasks:

• Architecture Support - 28 hours
• Writing a Path Search Algorithm - 49 hours
• Writing a Dodge Algorithm - 26 hours
• The rest is 67 hours

There are 3 main tasks in the list that took the most time: Architecture, Pathfinding, Dodges. In the "rest" there were such things as: balancing and fitting constants, editing bugs and algorithms that did not take much time.

Now you can go to the most interesting part - the algorithms, which I wrote quite a lot, and not all of them revealed their potential.

Algorithms

During the Olympiad, the following algorithms were implemented:

• Influence map - allows you to easily estimate the balance of forces along the lines and find the point where now stands on the line
• Prediction of the presence of the enemy in the invisible zone - you need first of all for a more accurate calculation of the map of influences
• Assessing the outcome of a local battle - you need to understand when to attack, and when to defend
• Projectile evasion is one of the most important algorithms.
• Finding the optimal position is the second most important algorithm. Evaluates where better to go and turn into the current tick. The weakest link of my strategy
• Finding a path - allows you to estimate the distance to a point and find which trees are in the way to reach it
• Obstacle avoidance - needed to circumvent nearby obstacles along the shortest path

Influence map

It was made after the first round. Initially created primarily for making tactical decisions in the final. In fact, its main purpose is to define the front line, the point where the battle is now taking place.

In addition, the influence map is important in assessing the outcome of a local battle, and assessing which line is best to stand on. It looks something like this:


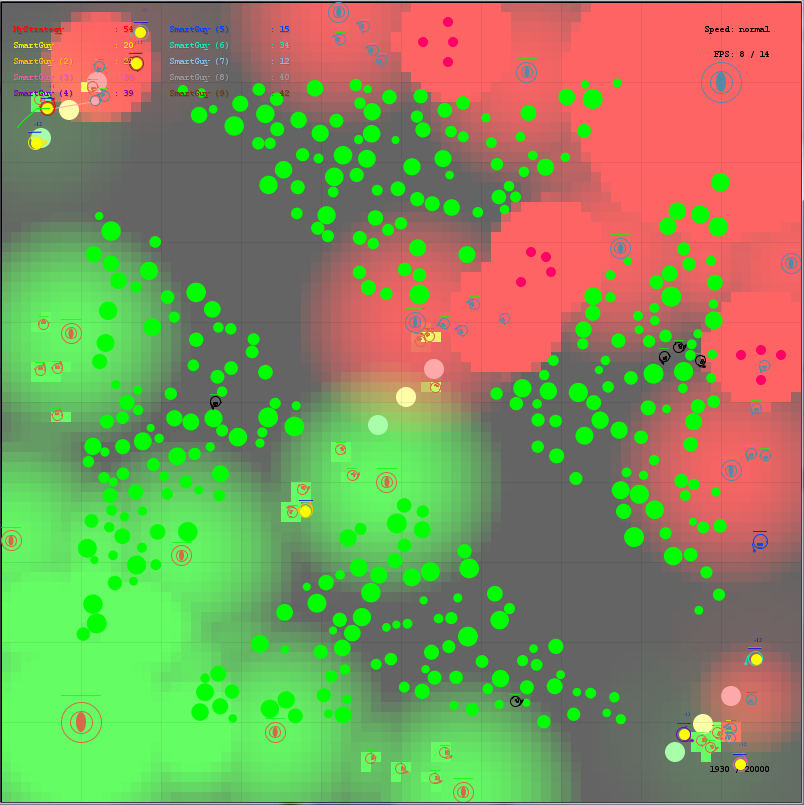
If you look closely, you can see that the main influence is made by creeps. Mages are a small influence due to their impermanence, and the towers are weak, and are not able to fight back in case of attack. In principle, the weakness of the towers is one of the biggest reasons for a different balance in the game than in MOBA.

It was built quite easily:

We pass through all units, buildings, magicians on the map, and fill the grid around. In total there are two grids: friendly and enemy, both grids of size 80x80 and on the whole map.

In order to find where the front line is now, the algorithm goes from its base to the enemy and checks the influence of enemies around the current verification point. If the enemy influence around this point is, then the front line at this point.

In fact, the algorithm initially acted on a different principle, and produced points where the “yellow” zone was encountered by the enemy for the first time. But the participant under the name core2duo changed my opinion about where the front line should be - his strategy in the final attacked the top tower, avoiding the forest and not going to the line, thereby passing the creeps past his magicians without paying attention to them.

Estimation on which side the preponderance of forces along the lines is obtained by using the sum of all the influences on this line. And with the help of the algorithm below, this estimate was accurate enough so that you can tell when the line starts to lose or, on the contrary, to win. True because of my laziness, the amount of influence is considered to be wrong, and how much stronger or weaker the line is not so easy to say.

Prediction of the enemy in the invisible zone

There are three predictions: finding enemy creeps, finding mages, towers. The first prediction is fairly accurate, but not directly used. It is only needed to estimate the strength of the line, since without this the algorithm would almost always consider that our lines win.

To predict enemy creeps, a fairly simple algorithm is used - once in 750 ticks, the time of creeps appearance, 4 creeps are always launched from the point of appearance, always in the same grouping, and with the same speed. As soon as they reach the zone where there is visibility, they disappear.

With magicians, another story is that they have little effect on the influence map, but sometimes it would be nice to be able to catch up with the enemy magician who ran off the edge of the screen. Therefore, all enemy magicians after their first appearance in the zone of visibility are saved in the local world, and if they disappeared from the zone of visibility, then there is an emulation of their withdrawal to the base. That is, the strategy always considers - if the mage is no longer visible, it means that he runs to the base.

Also, due to the fact that the towers shoot at the same distance as the radius of the mage, the positions of the enemy towers are hammered at the beginning of the game symmetrically with their own, in order to always know about their existence. Also for them is automatically considered the time to attack. Here the truth must be taken into account that it is necessary to take away dt and not 1, because if the magician died or was frozen, the strategy does not gain control over this magician.

Evaluation of the outcome of a local battle

Before the advent of this algorithm, my strategy always played against defense, the only case where a magician could attack was in cases of a front line displacement strongly towards the enemy base. Or the enemy magician himself came to be killed.

The emergence of this algorithm clearly gave an advantage among non-top strategies - the top strategies almost do not make mistakes and you can rarely say that if you attack, you will definitely win, but weaker strategies will make a mistake sooner or later and at that moment the predictor of the outcome of the battle will say - everything can attack.

Although he gave the main advantage in the attack, he was created primarily in order not to make mistakes in the imbalance on the line or, in a different way, if the enemy magicians are more than their own. In this case, it is better to stand slightly away from enemies, because if you make at least one mistake, then chances are good that your mage will be killed.

The method of calculating the outcome of a local battle is as simple as it can be, but despite this is quite effective.

First, we define the input parameters - at the entrance we have our magician and the point where we want to attack. There is also a more advanced option - your magician + enemy enters at the entrance, in which case the evaluation function of a chance to win is called twice - once for its own and once for an enemy magician. This approach helps to more accurately assess the chances of winning, rather than through a full stop, since in the case of equality of forces, he will give a number closer to zero, and in case of a big difference, on the contrary, heightens this difference even more.

The main calculation function looks like this:

1. If the current tick can cause me more damage than the mage xn, provided that everyone shoots him at the same time, then we return a negative chance of winning
2. We add the sum of the danger of friendly mages who are approximately at the same distance from the control point or closer than my magician.
3. We take away the sum of the danger of enemy magicians who are between their magician and the control point.
4. We add the advantage of forces in the circle of a given radius and in the center between the position of the magician and the control point.
5. Normalize the resulting values ​​and voila - there is a chance of victory.

The chance of winning is 100%, if the allied forces are more than one and a half magicians of the first level than the enemy forces.

Therefore, in games without a level, I do not often attack, because for an attack, the chance of winning must be more than 50%, which does not happen so often, provided that creeps make up about 20% of the power of one magician, and hp magicians are often equal.

The danger of a mage is estimated as the sum of 10 values: DPS, the presence of certain magic, the number of HP, the presence of buffs and debuffs, the cooldown of magic, the amount of mana. Each coefficient was chosen by eye and then slowly adjusted. In principle, writing more accurate coefficients in this place may not significantly improve the strategy.

Projectile evasion

The most effective algorithm of all existing, and at the same time almost the simplest.

Initially, the function of emulation of motion in a given direction was written for evasion. That is, the strategy estimates how much the projectile still has a maximum of ticks to fly and emulates, the movement of the magician in a certain direction, taking into account that he turns on each tick to him. If the projectile hit the magician, then this direction is wrong and you need to look in another direction. If a projectile hits in all directions, it is impossible to evade.

Initially, the strategy was considered in 3 directions, or in 6 if we consider the movements front and backwards in different directions. But after some time I realized that such evasions did not give time for an attack or retreat and began to consider where it is better to go, and then chase away the evasion for 60 directions in order to find the one that best matches the direction of motion.

Here is a weak point, I think the fact that when dodging, I always move and turn in one direction. In theory, this algorithm can be improved and find not the best movement deviation, but at the same time the minimum deviation in angle. Such an approach would increase the chances of winning a fight, since in order to shoot at an enemy it is necessary to make a turn to a smaller angle than with the current algorithm. This could save 2-3 ticks, which is very significant, provided that the magician can shoot every 60 ticks, and the projectile flies to the magician about 12 ticks.

But I did not describe one nuance - when dodging, it is necessary to take into account the obstacles around: trees, creeps, magicians, buildings. For these purposes, before counting the direction of motion, all intersections in this direction are sought, and the closest one to us is chosen. That is, the result is not a vector in which to move, but a segment. Since some of the objects each tick are shifted, but they do not have inertia, in order not to cut off the possibility of evasion once again, the radius of the object each tick decreases by the speed of the object. For mages, this is their maximum speed, and for creeps it depends on their direction of movement. So, if a creep was moving in our direction, then its radius would increase instead of decreasing. I ticked the “tick” in quotation marks, since there is no motion simulation there, for the place of this there is a formula that calculates the tick based on the distance to the intersection with the object.

Search for optimal position

If we consider the benefit of the algorithm as - the advantage given by the algorithm '/' number of lines of code ', then this is the most unnecessary algorithm. But, unfortunately, without him the magician could not move. All the commands in the move and defense folder + a couple of attack are responsible for counting the movement. More precisely, each team returns a vector, where it is necessary to move, the priority of movement in this direction and the same pair for rotation. Often the turn and movement are the same, but not always. The commands themselves are some complex functions that, by some criteria, consider these vectors. In total there are 9 movement teams:

• Chase the enemy mage
• Flee attack melee
• Keep your distance from the tower
• Keep away from creep
• Dodge the projectile
• Keep your distance from the enemy mage
• Run up to experience
• Run to the bonus
• Run to the front line

Almost each of them can be repeated, and they have a different priority, which in turn depends on different factors. For example, to attack melee chances of winning must be high. Or if the enemy magician can dodge the projectile, then we will shoot him last. Describing all the priorities may take another article, but there is almost no point in this - anyway, they were selected by eye.

After counting all such vectors, the strategy finds among them a mandatory one with maximum priority. If this is not the case, then it finds among all the vectors with the highest priority and averages it. Two types of vectors are considered obligatory - dodge from the projectile and escape from the tower. By averaging is meant the sum of vectors that are not more than 45 degrees deviated from the maximum and given their priority. This is done for greater accuracy, where to retreat if there are many almost identical vectors next to the magician - for example, near two enemy creeps. At the same time, it is not desirable to do this for obligatory vectors - they are calculated so that if they are not followed, then you can take damage.

Finding the way

The first version of the search for the path was quite simple, and was written before Round 1 - at a given point, which was about 50, a static graph was created, in which there was the shortest path to the point. Since the end point and the point where the magician is located were not on the way, from these points a perpendicular to the nearest given edges of the graph was constructed.

The biggest drawback that I saw in this approach was not the shortest path and to estimate the time it was possible to reach the point, a simple heuristic was written which gave a certain approximate coefficient - how much theoretically the shortest path differs from the calculated one.

Therefore, for round 2, a more difficult, but more accurate search of the path was written. In addition to a better estimate of the length of the path, he also allowed to evaluate the path, taking into account the cutting of trees, which in some cases saves time. The algorithm is a combination of Lee and Dijkstra and the principle of its work can be described as follows:

Create a 125x125 grid with prices on the map. Where there is no one - the price is 1, along the edges of the card the price is endless. After the price is added to the price for the passage through the tree, which depends on the radius of the tree - in the center of the tree it is maximum, and decreases to the edges. For creeps and towers are set almost infinite prices. Also, the influence map for the enemy side also refuses to have a small impact on prices in finding a way - you need this in order not to climb into the center of the battle, but to bypass it.

After that, a wave was launched from the current point of the magician, similar to the wave from the Lee algorithm, but it always started on the entire map, and took into account the weight of the transition to the cell. It is because of the transition weights that the algorithm itself still looks more like Dakesta than Lee:

1. A weighted map is created - all the weights are infinite, and a stack of transition points is created.
2. For the current point, set the weight to zero, and it is entered as a transition point.
3. In the loop, while there are transition points:
   
   
   1. We get the first transition point
   2. We look through all the neighbors (4 neighboring cells), and we consider the preliminary weights in these cells - the current weight of the cell + price from the neighbor
   3. If the resulting weight is less than the current weight in the cell, then we change the weight, and add the cell to the stack of transition points
   4. Go to the next iteration.

If we analyze this algorithm, then this implementation of the Lee algorithm, without taking into account the transition price, has an estimate of O (N * M), that is, each cell of the algorithm went around exactly once. You can also add the multiplier `* 4` as it checks the neighboring cells. Due to the presence of weights, the algorithm can visit each cell several times, but this is not critical. True, one limitation that Lee does not have is added - it is necessary to bypass the entire map. But for us this is not critical, since later on this map you can quickly find the way to any point, which, on average, is about 5 tick, and in extreme situations it can reach up to 10 or more.

To reduce construction time even more, this map is recalculated every 30 ticks. If the magician during this time changes the cell in which he is now located, then a quick weight change works out. The change of weight can be briefly described as follows: in the new cell we make the weight zero, in the old one we set the value slightly less than one. The value slightly less than one depends on how many times we changed the cell in the last 30 ticks. It is necessary that in the future, when searching for the path, the algorithm can always get to the current point, which is with zero weight.

The search for the path itself on the scale map is nothing complicated: From some point we construct the path so that we always choose the lowest price from the neighboring cells. True, there are already 8 neighbors, not 4, and for diagonal neighbors, the transition price is overstated by sqrt (2).

Chopping wood

After the path is built, you can request information about which trees to cut down. Any path is represented as a set of short segments that were built on the grid. These segments I will call segments. The following algorithm is used to obtain information about which trees are interfering with:

Go along the path and find the tree that is closest to our current path segment and not far from it. We are convinced that this tree actually suits us - it cannot be bypassed. For this, we figuratively divide our playing field into two parts - on one side of the road and on the other. If there is such a tree that belongs to the other side of the path and you cannot pass between these two trees, then the current tree must be chopped.

The truth is there is a problem - in places where the path passes close to the middle of the tree and the tree ends up not in the half of the way it would have cost, the tree may not be marked under the log house, despite the fact that it is. The reverse situation is also possible, when a tree does not seem to interfere, but it got into the wrong half of the way.

I closed my eyes to this problem - it was not critical, although it can be solved in a not very complicated way.

Obstacle avoidance

The very first algorithm that was written and the most unmodifiable. In fact, the pathfinding algorithm described above is not mandatory and was written from the calculations that the obstacle avoidance algorithm is already there and it is working.

On how the magician walks using only bypass obstacles can be viewed in the video . The video is slightly slowed down due to the fact that it was shot in debug mode.

The algorithm itself is based on the calculation of internal tangents between objects. This was possible, since all objects in the world are represented by circles.

The first thing that catches your eye when watching a video is the constantly twitching purple lines. The lines themselves were not used in the algorithm, but such a mapping turned out to be most effective in order to understand where there is a group of objects. To understand what a group of objects is, you can watch a video for 40 seconds - there the magician goes into the forest and passes between two groups. If you define something, groups of objects are non-intersecting subsets of the entire set of objects on the map, such that a magician can pass between any two objects from different subsets, or the distance between two objects is larger than the diameter of the magician + the radius of the first object + the radius of the second object.

The first part of the algorithm is building these groups. This is done like this:

First we have a set of objects and an empty set of groups. We take an object from a variety of objects and check that if it falls into one group, that is, it is close to one of the group objects, then we add it there. If it falls into more than one group, then we merge all such groups and add a new object to a new large group.

Next comes the definition of where to go in the current tick. This is done on the basis of: the set of groups, the position of the magician and the point where we want to come. I would call this algorithm this way - throwing rays, although in reality it’s still not rays, but segments, since they have max length.

1. First, we throw the beam to the point where we want to go.
2. We find the intersection with the group, the object from the group that is closest to us.
3. We pass through all the objects of the selected group and for each we consider both internal tangents.
4. We find the tangents that will give the maximum angle of deflection from the current beam - there will be two of them (one to the left and the other to the right).
5. Further, according to the magic logic (see below), we choose one of the two.
6. The point of contact, taking into account the radius of the magician, will be our new point where we need to move.
7. After that, we again throw the beam, but at a new point, after removing the group with which we have already crossed.

To understand the reason for the existence of "magical logic", let's look at the picture:

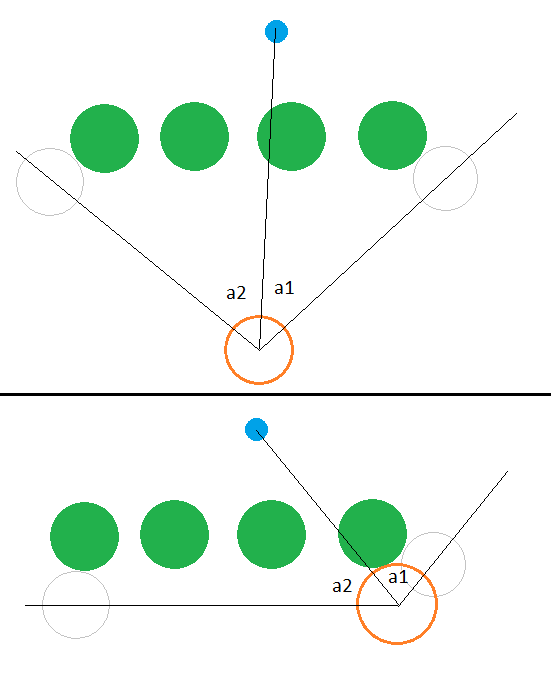
Initially, the angle a1 is less than the angle a2, and it is more logical to go towards the angle a1, since there should be a shorter path, but as you approach the tangency point, the angle a1 starts to increase, and the angle a2 decreases. For this reason, the whole magical logic was that not only the angle, but also the distance was taken into account. After the appearance of the search path, this problem has disappeared, since the beam itself was already close to the ideal.

As a conclusion

If you compare my solution with the solution of Commandos (second place in the final, but we know that in fact the first), then its solution is more concise and simple, but it does not allow you to make tactical assessments, but it gives an almost perfect solution in local battles . All my algorithms are tied to the adoption of tactical decisions and the game throughout the map, rather than for local battles. At the same time, the very local battles I have made are very difficult and cumbersome.

For this reason, I decided to describe my decision - I have a different direction compared to the decisions of the top players.

For those who want to write the Olympiad next year, and the number of people is growing from year to year, I advise you to sleep at night ... It’s better to spend two hours on the code, but it will be good rather than write at night and then look for bugs in the code during the week.For myself, I made exactly this conclusion when I looked through my code in a “sober” state. Actually the code itself can be viewed here: github.com/ivlevAstef/CodeCupAI2016MOBA . There are many comments in Russian that can help you understand the code. True to understand the architecture will have to spend time.


I also want to mention the participant with the nickname firano (Leonid Lobanov) for his unbearable help with writing this article.

And many thanks to Roman Udovichenko ( Romka ) for organizing the chat in a telegram and to all the active participants in this chat. Without you, writing the Olympiad would be much more boring, albeit more productive.