Coding with the withdrawal of information. Part 1, philosophical

Written in collaboration with Revaz Bukhradze and Kirill Perminov

1. Introduction

Offline messaging is now one of the most popular ways to communicate ( 1 , 2 , 3 ) - judging by the audience ways to communicate and the dynamics of its growth.

In this case, the key requirement in the exchange of messages will always be the full compliance of the sent message - received, that is, the transfer of data should not irreversibly distort the data itself. Natural desire - to save led to the creation of data compression algorithms, which remove the natural redundancy of data minimizing the amount of stored and transmitted files.

The maximum amount of compression that guarantees unambiguous data recovery is determined by the works of K. Shannon on information theory, and in general is insurmountable since the removal of not only redundant, but also semantic information will not allow unambiguously to restore the original message. It is worth noting that the refusal of accurate recovery in some cases is not critical and is used to effectively compress graphics , video and music data, where the loss of non-essential elements is justified, but in the general case, data integrity is more important than their size.

Accordingly, the interesting question is whether it is possible, without violating the provisions of the theory of information, to transmit a message with a volume less than the minimum volume that can be achieved with the best data compression.

2. Example

Therefore, let's analyze an example that will allow us to study the features of information transfer. And although in the “English” tradition of information exchange participants it is accepted to call Alice and Bob , we will use the more familiar message lovers on the eve of the new year: Matroskin and Sharik, respectively.

As a message, we choose m : “ , , ! ". Its length in single-character encoding- len (m) is 34 bytes.

You may notice that the length of the message is noticeably more than the amount of information in it. You can check this by deleting every tenth character from the message first, then every 9th (again from the original message) and so on up to every fourth, the result will be - “ , ! "-26 bytes. Accordingly, the degree of "mystery" will gradually increase, but, guess what it is, it will be quite simple. Moreover, Yandex recognizes this appeal .

Even a higher degree of reduction in the length of the message while maintaining the meaning can be achieved by discarding the vowels and part of the spaces: “ ,, ! ”- 21 bytes, it is worth noting that although search engines do not cope with such writing, it is not difficult to restore the phrase.

If we look at the amount of information I (m) in this message, defined more strictly through the concept of information entropy , it is clear that the amount of information transmitted in this message is approximately 34 * 4.42 / 8 = 18.795 bytes. Here: 4.42 bits / symbol is the average amount of information in one byte of the Russian language ( 4 , 5 ), and 8 is the conversion from bits to bytes. This shows that using the best method of data compression will need to spend at least 19 bytes to send a message from Matroskin to Sharik.

Moreover, the converse is also true that it is impossible to transmit the message we need without losses in less than 19 bytes (C. Shannon, Works on Information Theory and Cybernetics., Ed. Foreign Literature, Moscow, 1963). Theorem 4. p 458.

3. Further reasoning

But let's continue ... Let Matroskin and Sharik have some additional information k and a couple of functions, one of which is m '= E (k, m) , which calculates the intersection of additional information k and the original message m 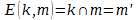and the second D (k, m ') = m is the inverse of E. Moreover, the amount of information determined by Shannon satisfies the following condition: . Accordingly, if we manage to construct the pair of functions E (k, m) and * D (k, m ') defined above, such that the following two conditions are fulfilled:

• ,
• 

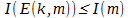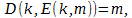
then this will mean that in order to transfer information between recipients it may require less information than is contained in the original message.

In this case, it is worth paying attention to the fact that, by the definition of these functions, there is no violation of the statements of information theory.

Similar, algorithms involving the replacement of transmitted information with its hash are actively used in network traffic optimization systems . At the same time, however, unlike the algorithm described, in order to effectively use this type of optimization, at least a single data transfer is required.

Since natural language messages contain more data than information, preliminarily compressing the original message using any of the algorithms that effectively eliminate redundancy, such as arithmetic coding .

Denote the application of the compression operation m '= Ar (m) such that 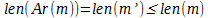. If we now use the function E defined above over a pre-compressed message, we can see that the amount of data transmitted and the amount of information transmitted between the recipients may be less than the amount of data and the amount of information in the original message.

That is, summarizing: assuming that there is an invertible transformation D (k, E (k, m)) = m , such that 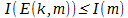the use of redundancy operations makes it possible to transmit the amount and amount of information in a volume not exceeding the corresponding parameters ( len (m) length and information amount I (m) ) of the original message.

In general, it remains only to choose the function ... ..