Recognition of radio signals using neural networks

The topic of signal recognition is very relevant. Signal recognition can be used in radar to identify objects, for decision-making tasks, medicine, and many other areas.

Research areas

I believe that research should be conducted in two directions. The first direction is the primary signal processing, in which the signal in the time domain "s (t)" is replaced by functionals. [5] A set of functionals is a vector in the feature space by which recognition takes place.

The second direction is the research and development of the classifiers themselves, since classes in the feature space can have non-linear separation. Neural networks of the perceptron type are capable of dividing only linearly separable classes. And neural networks of the type of radial basis networks, are able to divide only classes with spherical separation. [4]

Often these two types of neural networks combine. It is very important to choose the feature space correctly, because if there is excessive information about the signal, it will complicate the recognition procedure due to the fact that the classes will be difficult to separate: they can be either non-linearly separable or not separable at all. If there is not enough data, it will be problematic to recognize an object, due to the fact that several signals correspond to one data set. For recognition, as a sign, you can enter the statistical parameters of the signals.

I propose to introduce the following criteria by which to determine the number of signs:

1) Signs must be different for objects belonging to different classes.
2) They must coincide in their value for objects of the same class.

Full coincidence of statistical parameters of signals is possible only if the signal is ergodic and the observation time tends to infinity. The non-ergodic signal, or the signal, the observed finite time forms a certain area in the multidimensional feature space. [3]

Signals belonging to different classes form their own areas. The task of the classifier is to separate one region from another. The task of preprocessing is reduced to describing a signal with a finite vector, so that signals belonging to the same class are close to each other in multidimensional Euclidean space, and signals belonging to different classes are far away, in other words so that the compactness hypothesis is fulfilled. [1]

It should be noted that signals are almost always recorded against the background of noise, and methods of recognition based on Fourier transforms or recognition by samples in the time domain imply filtering the signal as the primary processing. [5] The recognition method based on statistics does not need filtering if the disturbance is an ergodic random process. Since You can always "subtract" from the signal model with the interference model interference. [2]

Important! This method can not recognize biological signals. Since biological signals are very specific, for their recognition it is necessary to take into account the mechanics of the processes generating these signals. [6] Let's say the ECG signal and the EEG signal are investigated by various methods.

Mathematical foundations

In practice, it turned out that to solve most of the recognition problems, it is enough to use only 4 parameters for recognition, such as: mat. waiting, sko, kurtosis and asymmetry.

For example, consider the recognition of the signal with the following options:

1) no signal (disturbance only)
2) sine wave + noise
3) rectangular + noise
4) radio pulse with a rectangular envelope + interference.
S / N ratio ( 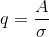in experiment it is 0.2.
We take the signal amplitude equal to 1 Volt (so as not to normalize), and the noise in the form of white noise with a normal distribution.

For recognition, we will use a double-layer perceptron, with 4 inputs, 4 outputs and 9 neurons on a hidden layer (a sufficient condition by the Kolmogorov theorem). [4]

Primary processing

Let's make a vector in the feature space, for the beginning we will determine the noise model:

[2,3]

Now create a vector for the signal with noise:

m is the mathematical expectation, D is the variance, - SKO, - kurtosis - asymmetry.

But this was the case with continuous signals, and when the analytical expression of the probability density f (x) is known. With a discrete signal, the integral is replaced by a sum. And we are not talking about statistical parameters, but about their estimates. [2] And there the errors of determining the estimates come into force (we will talk about them in another article).

N is the number of counts.

After that we can form the input vector for the neural network.

Variables with an index of "x" are the components of the input vector, without an index — characteristics of the signal with noise, and with an index "noise model. To normalize the MSE, another 2.5 is divided.

Practical implementation

Here is the interface of the test program.

In this experiment, the probability of correct recognition was 94.6%. The neural network was trained by the gradient descent method on a sample of 50 implementations per signal, in a 2001 signal count.

Literature:

1. Classification. Compactness hypothesis
2. Wentzel E.S. Probability Theory: Textbook. for universities. - 6th ed. erased - M .: Higher. shk., 1999.
3. IN AND. Tikhonov. Statistical radio engineering.
4. Stanislav Osovsky. Neural networks for information processing.
5. A.M. Deutsch Identification methods for dynamic objects
6. Sinyutin S. A. Designing of microcontroller systems for the acquisition, processing and analysis of electrocardiogram.