Programming multi-core DSP processors TMS320C66x using OpenMP
The article describes the approach to programming multi-core signal processors based on OpenMP. OpenMP directives are considered, their meaning and use cases are analyzed. The emphasis is on digital signal processors. Examples of the use of OpenMP directives are chosen close to the tasks of digital signal processing. The implementation is carried out on a TMS320C6678 processor by Texas Instruments, which includes 8 DSP cores. Part I of the article discusses the basic OpenMP directives. In Part II of the article, it is planned to supplement the list of directives, as well as consider the issues of the internal organization of OpenMP work and the issues of software optimization.
This article reflects the lecture and practical material offered to students in the framework of refresher courses on the program "Multi-core processors of digital signal processing C66x company Texas Instruments" held annually in the Ryazan University of Radio Engineering. The article was planned for publication in one of the scientific and technical journals, but due to the specifics of the issues under consideration, it was decided to accumulate material for a textbook on multi-core DSP-processors. In the meantime, this material will accumulate, it may well lie on the Internet pages in the public domain. Feedback and suggestions are welcome.
The modern industry of high-performance processor elements is currently experiencing a characteristic turn associated with the transition to multi-core architectures [1, 2]. This transition is a measure rather forced than the natural course of processor evolution. Further development of semiconductor technology along the path of miniaturization and increase in clock frequencies with a corresponding increase in computational performance was impossible due to a sharp decrease in their energy efficiency. The logical way out of the current situation is that the manufacturers of processor technology considered the transition to multi-core architectures, allowing the processor to increase the computing power not due to the faster operation of its elements, but due to the parallel operation of a large number of operating devices [1]. This turn is typical for processor technology in general, and, in particular, for digital signal processing processors with their specific applications and special requirements for computational efficiency, efficiency of internal and external data transmissions with simultaneous low power consumption, size and price.
From the point of view of the developer of real-time signal processing systems, the transition to the use of multicore architectures of digital signal processors (DSP) can be expressed in three main problems. The first is the development of the hardware platform, its capabilities, the purpose of certain units and their modes of operation, established by the manufacturer [1]. The second is the adaptation of the processing algorithm and the principle of system organization for implementation on a multi-core DSP (MSCP) [3]. The third is the development of software (software) for digital signal processing implemented on the MTSSP. At the same time, software development for the MSCP has a number of fundamental differences from the development of traditional single-core applications, including the distribution of certain code fragments by core, data separation, core synchronization, data and service information exchange between cores, cache synchronization and others.
')
One of the most attractive solutions for porting existing “single-core” software to a multi-core platform or for developing new “parallel” software products is the Open Multi-Processing Toolkit (OpenMP). OpenMP is a set of compiler directives, functions, and environment variables that can be embedded in standard programming languages, primarily in the most common C language, expanding its capabilities by organizing parallel computing. This is the main advantage of the OpenMP approach. No need to invent / learn new parallel programming languages. A single-core program easily becomes multi-core by adding simple and clear directives to the compiler in standard code. All that is needed is for the compiler of this processor to support OpenMP. That is, processor manufacturers should take care that their compilers "understand" the OpenMP standard directives and translate them into appropriate assembler codes.
The OpenMP standard is developed by an association of several large computer manufacturers and is regulated by the OpenMP Architecture Review Board (ARB) [4]. At the same time, it is universal, not intended for specific hardware platforms of specific manufacturers. The ARB organization openly publishes the specification of the next versions of the standard [5]. Also of interest is the OpenMP quick reference [6].
Recently, an enormous number of papers [7–12] have been devoted to the use of OpenMP in various applications and on various platforms. Of particular interest are books that allow you to fully get a basic knowledge of using OpenMP. In the domestic literature, these are sources [13–16].
This paper is devoted to the description of OpenMP directives, functions and environment variables. In this case, the specifics of the work is its focus on the tasks of digital signal processing. Examples illustrating the meaning of certain directives are taken with an emphasis on implementation on the MTSSP. As a hardware platform, MTSC TMS320C6678 processors from Texas Instruments [17] were selected, including 8 DSP cores. This platform MTSSP is one of the best, enjoying wide demand in the domestic market. In addition, the paper discusses a number of issues related to the internal organization of OpenMP mechanisms that are relevant to the tasks of processing real-time signals, as well as optimization issues.
So, let the processing task is to form the output signal, as the sum of two input signals of the same length:
A “single core” implementation of this task in the standard C / C ++ language might look like this:
Suppose now we have an 8-core processor TMS320C6678. The question arises, how to use the capabilities of a multi-core architecture for the implementation of this program?
One solution is to develop 8 separate programs and independently load them into 8 cores. This is fraught with the presence of 8 separate projects in which it is necessary to take into account joint rules of execution: the location of arrays in memory, the separation of parts of arrays between cores, and so on. In addition, it will be necessary to write additional programs that synchronize the kernels: if one core has completed the formation of its part of the array, this does not mean that the entire array is ready; it is necessary either to manually check the completion of all cores, or to send processing completion flags to one “main” core from all cores, which will issue a corresponding message about the output array readiness.
The described approach can be correct and effective, however, it is rather difficult to implement and in any case requires the developer to significantly revise the existing software. We would like to be able to go from single-core to multi-core implementation with minimal changes to the source code! This is the task that OpenMP solves.
Before you start using OpenMP in your program, you obviously need to connect this functionality to your project. For TMS320C6678 processors, this means modifying the project configuration file and the platform used, and including references to OpenMP components in the project properties. We will not discuss such specific hardware-specific settings in the article. Consider the more general initial OpenMP settings.
Since OpenMP is an extension of the C language, the inclusion of its directives and functions in its program must be accompanied by the inclusion of a file describing this functionality:
Next, you need to tell the compiler (and the OpenMP functionality) how many cores we are dealing with. Note that OpenMP does not work with kernels, but with parallel threads. Parallel flow is a logical concept, and the core is physical, hardware. In particular, several parallel threads can be implemented on one core. At the same time, truly parallel execution of the code naturally implies that the number of parallel threads coincides with the number of cores, and each thread is implemented on its own core. In the future, we will assume that the situation looks exactly like this. However, it should be borne in mind that the number of a parallel thread and the number of its core does not have to be the same!
To the initial OpenMP settings, we assign the task of the number of parallel streams using the following OpenMP function:
We set the number of cores (threads) to 8.
So, we want the program code above to run on 8 cores. With OpenMP, it’s enough just to add the parallel directive to the code as follows:
All OpenMP directives are issued in the form of the following constructs:
In our case, we do not use any options, and the parallel directive means that the code snippet following it, marked with curly brackets, refers to a parallel region and must be executed not on one, but on the entire specified number of cores.
We received a program that runs on one main or master core (master core), and those fragments allocated by the parallel directive run on a given number of cores, including both the master and slave cores. In the resulting implementation, the same vector summation cycle will be executed immediately on 8 cores.
A typical structure for the organization of parallel computing in OpenMP is shown in Figure 1.
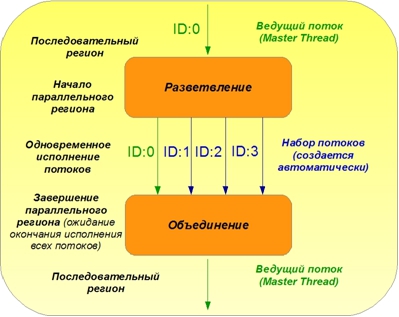
Figure 1. The principle of parallel computing in OpenMP
The execution of a program code always begins with a sequential region, executed on a single core in a leading thread. At the point of beginning of a parallel region, indicated by the corresponding OpenMP directive, the organization of parallel execution following the OpenMP directive of the code in the stream set (parallel region) occurs. The figure shows only four parallel streams for simplicity. At the end of a parallel region, the flows merge, waiting for each other’s work to finish, and then a successive region follows again.
So, we managed to use 8 cores for the implementation of our program, however, there is no sense in such parallelization, since all cores do the same work. 8 cores 8 times formed the same output data array. The processing time did not decrease. Obviously, it is necessary to somehow divide the work between different cores.
Let's draw an analogy. Let there be a team of 8 people. One of them is paramount; the rest are his assistants. They receive requests for various works. The main worker accepts and executes orders, connecting, whenever possible, his assistants. The first job that our employees took up was to translate text from English into Russian. The brigadier took up the work, took the source text, prepared the dictionaries, copied the text for each of his assistants and distributed to everyone the same text, without dividing the work between them. The translation will be completed. The task will be solved correctly. However, there will be no gain from having 7 helpers. Quite the contrary. If they have to share the same dictionary, or a computer, or a sheet with the source text, the task execution time may be delayed. OpenMP also works in our first example. Requires separation of work. Each employee should indicate which fragment of the general text he should translate.
An obvious way to divide work between kernels in the context of the task of summing arrays is to distribute loop iterations among the cores depending on the core number. It is enough to find out inside which parallel code the code is running inside the parallel region, and specify a range of loop iterations depending on this number:
The kernel number is read by the OpenMP function omp_get_thread_num () ;. This function, being inside a parallel region, runs the same on all cores, but on different cores gives a different result. Due to this, it becomes possible to further divide the work within the parallel region. For simplicity, we assume that the number of iterations of the cycle N is a multiple of the number of kernels. The reading of the core number can be hardware based on the presence in each core of a special register core number - the DNUM register on TMS320C6678 processors. It can be accessed by various means, including assembler commands or CSL support library functions. However, you can use the functionality provided by the OpenMP add-in. Here, however, we must again pay attention to the fact that the kernel number and the number of the parallel OpenMP region are different concepts. For example, the 3rd parallel thread may well run on, say, the 5th core. Moreover, in the next parallel region or with the repetition of the same parallel region, the 3rd stream can already be executed on, for example, the 4th core. And so on.
We got a program running on 8 cores. Each core processes its part of the input arrays and forms the corresponding area of the output array. Each of our employees translates their 1/8 part of the text and, ideally, we get an 8-fold acceleration of the solution of the problem.
We looked at the simplest parallel directive, which allows to extract fragments in code that should be executed on several cores in parallel. This directive, however, implies that all cores execute the same code and no work separation is provided for. We had to do it on our own, which looks a bit confusing.
Automatic indication of how work within a parallel region is divided between the cores is possible using the additional for directive. This directive is used inside a parallel region immediately before loops such as for and says that loop iterations should be distributed between the cores. The parallel and for directives can be used separately:
And can be used together in a single directive to reduce the record:
The use of the parallel for directive in our example of adding arrays leads to the following program code:
If we compare this program with the original single-core implementation, we will see that the differences are minimal. We just connected the header file omp.h, set the number of parallel threads and added one line - the parallel for directive.
Work sharing between cores can be done either on the basis of data sharing, or on the basis of task sharing. Recall our analogy. If all workers do the same thing - they are engaged in translating text - but each translates a different piece of text, then this refers to the first type of work sharing - data separation. If workers perform various actions, for example, one translates the entire text, another searches for words in the dictionary, a third types the translation, and so on, then this refers to the second type of work division - task separation. The parallel and for directives we considered allowed us to separate the work by dividing the data. The separation of tasks between the cores allows you to execute the sections directive, which, as in the case of the for directive, can be used independently of the parallel directive or in conjunction with it to shorten the record:
and
As an example, we present a program that uses 3 processor cores, and each of the cores performs its own algorithm for processing the input signal x:
We choose to consider a new example. Let us turn to the calculation of the scalar product of two vectors. A simple C program that implements this procedure may look like this:
The result of the execution (for test arrays of 16 elements) turned out to be equal to:
Let us turn to the parallel implementation of this program, using the parallel for directive:
Result of performance:
The program gives the wrong result! Why?
To answer this question, it is necessary to understand how the values of variables in the serial and parallel regions are related. We describe the logic of OpenMP in more detail.
The dotp () function starts to run as a sequential region on the 0th processor core. At the same time, in the memory of the processor, arrays x and y are organized, as well as variables I and sum. When the parallel directive is reached, the OpenMP utility functions come into play and organize the subsequent parallel operation of the kernels. There is an initialization of the cores, their synchronization, data preparation and a general start. What happens to variables and arrays?
All objects in OpenMP (variables and arrays) can be divided into common (shared) and private (private). Shared objects are located in shared memory and are used equally by all cores within a parallel region. Common objects coincide with objects of the same name in a sequential region. They move from sequential to parallel region and back unchanged, while maintaining their value. Access to such objects within a parallel region is equal for all cores, and there may be conflicts of general access. In our example, the x and y arrays, as well as the variable sum, turned out to be common by default. It turns out that all cores use the same variable sum as a battery. As a result, sometimes a situation arises in which several cores simultaneously read the same current value of the battery, add their partial contribution to it and write a new value to the battery. In this case, the core that records last, erases the work of the other cores. It is for this reason that our example gave the wrong result.
The principle of working with public and private variables is illustrated in Figure 2.
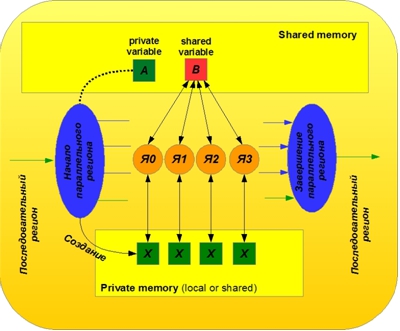
Figure 2. Illustration of OpenMP operation with public and private variables
Private objects are copies of the original objects, created separately for each kernel. These copies are created dynamically when initializing a parallel region. In our example, the variable i as a loop iteration count is considered private by default. When the parallel directive is reached, 8 copies (by the number of parallel threads) of this variable are created in the processor's memory. Private variables are located in the private memory of each kernel (they can be located in local memory, or they can also be shared, depending on how we declared them and configured the memory). Private copies by default are not related to the source objects of the sequential region. By default, the values of the source objects are not transferred to the parallel region. What private copies of objects are at the beginning of a parallel region is unknown. At the end of a parallel region, the values of private copies are simply lost, unless special measures are taken to transfer these values to a sequential region, which we will discuss later.
To explicitly tell the compiler which objects should be considered private and which should be shared, the options shared and private are used in conjunction with the OpenMP directives. The list of objects belonging to the public or private is indicated by a comma in brackets after the corresponding option. In our case, the variables i and sum should be private, and the arrays x and y should be common. Therefore, we will use the construction of the form:
when opening a parallel region. Now each core will have its own battery, and accumulations will go independently of each other. Additionally, the batteries must now be reset, since their initial value is unknown. In addition, the question arises how to combine the particular results obtained on each of the nuclei. One option is to use a special common array of 8 cells, in which each core will place its result inside a parallel region, and after leaving the parallel region, the main core summarizes the elements of this array and forms the final result. We get the following program code:
Result of performance:
The program works correctly, although it is a bit cumbersome. We will discuss further how to simplify it.
It is interesting that when specifying the names of OpenMP arrays as private objects during initialization of a parallel region, it acts the same way as with variables — it dynamically creates private copies of these arrays. You can verify this by conducting a simple experiment: declaring an array through the private option, print the values of the pointers to this array in the sequential and parallel regions. We will see 9 different addresses (with the number of cores - 8).
Next, you can make sure that the values of the elements of the arrays are not related to each other. In addition, when you later enter the same parallel region, the addresses of private copies of the arrays may be different, and the default values of the elements are not saved. All this leads us to the fact that OpenMP directives that open and close a parallel region can be quite cumbersome and require a specific execution time.
If there is no explicit indication of its type (common / private) for an object in the opening directive of a parallel region, then OpenMP “acts” according to certain rules described in [5]. Undefined objects OpenMP refers to the default type. What type it will be, private or shared, is determined by the environment variable — one of the OpenMP operation parameters. . , . . for parallel for, .
default. , – . , none, , , , :
or:
In the considered example of the implementation of the scalar product on 8 cores, we noted one drawback: combining the private results of the cores requires significant code modifications, which makes it cumbersome and inconvenient. At the same time, the openMP concept implies maximum transparency in the transition from single-core to multi-core implementation and vice versa. Simplify the program discussed in the previous section, allows the use of the reduction option.
The reduction option allows the compiler to indicate that the results of the kernels should be combined, and sets the rules for such a combination. The reduction option is provided for a number of the most common situations. The option syntax is as follows:
reduction, OpenMP , 1.
: +, *, -, &, |, ^, &&, ||, max, min
: 0, 1, 0, 0, 0, 0, 1, 0, , .
reduction c «+» sum:
Result of performance:
«» !
, , . , , . , , . , . .
, , ( ) , . , , . , ( ), , . -: , , . , OpenMP- , . , , - - () .
In OpenMP, two types of synchronization can be distinguished: implicit and explicit. Implicit synchronization occurs automatically at the end of parallel regions, as well as at the end of a number of directives that can be applied within parallel regions, including omp for, omp sections, and so on. This automatically synchronizes the cache.
If the problem solving algorithm requires synchronizing the kernels in those points of the program inside a parallel region where automatic synchronization is not provided, the developer can use explicit synchronization — tell the OpenMP compiler explicitly using special directives that synchronization is required at this point. Consider the main of these guidelines.
The barrier directive is written as:
and explicitly sets the synchronization point for parallel OpenMP threads within a parallel region. Let's give the following example of using the directive:
. z, z, z. z, . : . z, . . barrier . z . , , , . , z, , . barrier z. – .
The critical directive is written as:
And selects a code fragment inside a parallel region, which can be executed at a time by only one core.
, . . , , , , . , . , . , , : , , ; .
. , , critical. :
() Z. 8 . , . , . Z. , . , . , ( ), , . . , .
Let's replace the critical section in our code with the following construction.
Now we have two critical sections. In one, the results of the work of the nuclei are combined by summation; in the other, by multiplication. Both sections can run simultaneously on only one core, however, different sections can run simultaneously on different cores. If you enter the name of a region into the construction of the directive critical, then the kernel will be denied access to the code only if another core works in this particular region. If the names of the regions are not assigned, then the kernel will not be able to enter any of the critical regions if the other core works with any of them, even if they are not related to each other.
The atomic directive is written as:
In the previous example, different kernels were forbidden to execute code from the same region at the same time. However, this may not seem rational on closer examination. After all, access conflicts to a shared resource consist in the fact that different cores can simultaneously access the same memory cells. If, within the same code, the call goes to different memory cells, the result will not be distorted. The atomic directive allows the synchronization of cores to memory elements. It indicates that in the next line of the memory operation is atomic - inseparable: if some core starts operation with a certain memory cell, access to this memory cell will be closed for all other cores until the first core finishes working with her. At the same time, the atomic directive is accompanied by options indicatingWhat type of operation is performed with memory: read / write / modify / capture. The above example when applying the atomic directive will look like this.
, atomic , , . . , , atomic , , , . , critical MxT1 , – , T1 – ; atomic 2 . atomic , 2 , 1.
OpenMP – (/++), , , . 8- TMS320C6678 Texas Instruments. OpenMP – . , , OpenMP, . . OpenMP . .
, , OpenMP , . , , .
, OpenMP . OpenMP OpenMP . OpenMP 1 2, Texas Instruments TMS320C6678 . . OpenMP; , ; OpenMP; .
This article reflects the lecture and practical material offered to students in the framework of refresher courses on the program "Multi-core processors of digital signal processing C66x company Texas Instruments" held annually in the Ryazan University of Radio Engineering. The article was planned for publication in one of the scientific and technical journals, but due to the specifics of the issues under consideration, it was decided to accumulate material for a textbook on multi-core DSP-processors. In the meantime, this material will accumulate, it may well lie on the Internet pages in the public domain. Feedback and suggestions are welcome.
Introduction
The modern industry of high-performance processor elements is currently experiencing a characteristic turn associated with the transition to multi-core architectures [1, 2]. This transition is a measure rather forced than the natural course of processor evolution. Further development of semiconductor technology along the path of miniaturization and increase in clock frequencies with a corresponding increase in computational performance was impossible due to a sharp decrease in their energy efficiency. The logical way out of the current situation is that the manufacturers of processor technology considered the transition to multi-core architectures, allowing the processor to increase the computing power not due to the faster operation of its elements, but due to the parallel operation of a large number of operating devices [1]. This turn is typical for processor technology in general, and, in particular, for digital signal processing processors with their specific applications and special requirements for computational efficiency, efficiency of internal and external data transmissions with simultaneous low power consumption, size and price.
From the point of view of the developer of real-time signal processing systems, the transition to the use of multicore architectures of digital signal processors (DSP) can be expressed in three main problems. The first is the development of the hardware platform, its capabilities, the purpose of certain units and their modes of operation, established by the manufacturer [1]. The second is the adaptation of the processing algorithm and the principle of system organization for implementation on a multi-core DSP (MSCP) [3]. The third is the development of software (software) for digital signal processing implemented on the MTSSP. At the same time, software development for the MSCP has a number of fundamental differences from the development of traditional single-core applications, including the distribution of certain code fragments by core, data separation, core synchronization, data and service information exchange between cores, cache synchronization and others.
')
One of the most attractive solutions for porting existing “single-core” software to a multi-core platform or for developing new “parallel” software products is the Open Multi-Processing Toolkit (OpenMP). OpenMP is a set of compiler directives, functions, and environment variables that can be embedded in standard programming languages, primarily in the most common C language, expanding its capabilities by organizing parallel computing. This is the main advantage of the OpenMP approach. No need to invent / learn new parallel programming languages. A single-core program easily becomes multi-core by adding simple and clear directives to the compiler in standard code. All that is needed is for the compiler of this processor to support OpenMP. That is, processor manufacturers should take care that their compilers "understand" the OpenMP standard directives and translate them into appropriate assembler codes.
The OpenMP standard is developed by an association of several large computer manufacturers and is regulated by the OpenMP Architecture Review Board (ARB) [4]. At the same time, it is universal, not intended for specific hardware platforms of specific manufacturers. The ARB organization openly publishes the specification of the next versions of the standard [5]. Also of interest is the OpenMP quick reference [6].
Recently, an enormous number of papers [7–12] have been devoted to the use of OpenMP in various applications and on various platforms. Of particular interest are books that allow you to fully get a basic knowledge of using OpenMP. In the domestic literature, these are sources [13–16].
This paper is devoted to the description of OpenMP directives, functions and environment variables. In this case, the specifics of the work is its focus on the tasks of digital signal processing. Examples illustrating the meaning of certain directives are taken with an emphasis on implementation on the MTSSP. As a hardware platform, MTSC TMS320C6678 processors from Texas Instruments [17] were selected, including 8 DSP cores. This platform MTSSP is one of the best, enjoying wide demand in the domestic market. In addition, the paper discusses a number of issues related to the internal organization of OpenMP mechanisms that are relevant to the tasks of processing real-time signals, as well as optimization issues.
Formulation of the problem
So, let the processing task is to form the output signal, as the sum of two input signals of the same length:
z(n) = x(n) + y(n), n = 0, 1, …, N-1 A “single core” implementation of this task in the standard C / C ++ language might look like this:
void vecsum(float * x, float * y, float * z, int N) { for ( int i=0; i<N; i++) z[i] = x[i] + y[i]; } Suppose now we have an 8-core processor TMS320C6678. The question arises, how to use the capabilities of a multi-core architecture for the implementation of this program?
One solution is to develop 8 separate programs and independently load them into 8 cores. This is fraught with the presence of 8 separate projects in which it is necessary to take into account joint rules of execution: the location of arrays in memory, the separation of parts of arrays between cores, and so on. In addition, it will be necessary to write additional programs that synchronize the kernels: if one core has completed the formation of its part of the array, this does not mean that the entire array is ready; it is necessary either to manually check the completion of all cores, or to send processing completion flags to one “main” core from all cores, which will issue a corresponding message about the output array readiness.
The described approach can be correct and effective, however, it is rather difficult to implement and in any case requires the developer to significantly revise the existing software. We would like to be able to go from single-core to multi-core implementation with minimal changes to the source code! This is the task that OpenMP solves.
OpenMP Initial Settings
Before you start using OpenMP in your program, you obviously need to connect this functionality to your project. For TMS320C6678 processors, this means modifying the project configuration file and the platform used, and including references to OpenMP components in the project properties. We will not discuss such specific hardware-specific settings in the article. Consider the more general initial OpenMP settings.
Since OpenMP is an extension of the C language, the inclusion of its directives and functions in its program must be accompanied by the inclusion of a file describing this functionality:
#include <ti/omp/omp.h> Next, you need to tell the compiler (and the OpenMP functionality) how many cores we are dealing with. Note that OpenMP does not work with kernels, but with parallel threads. Parallel flow is a logical concept, and the core is physical, hardware. In particular, several parallel threads can be implemented on one core. At the same time, truly parallel execution of the code naturally implies that the number of parallel threads coincides with the number of cores, and each thread is implemented on its own core. In the future, we will assume that the situation looks exactly like this. However, it should be borne in mind that the number of a parallel thread and the number of its core does not have to be the same!
To the initial OpenMP settings, we assign the task of the number of parallel streams using the following OpenMP function:
omp_set_num_threads(8); We set the number of cores (threads) to 8.
Parallel directive
So, we want the program code above to run on 8 cores. With OpenMP, it’s enough just to add the parallel directive to the code as follows:
#include <ti/omp/omp.h> void vecsum (float * x, float * y, float * z, int N) { omp_set_num_threads(8); #pragma omp parallel { for ( int i=0; i<N; i++) z[i] = x[i] + y[i]; } } All OpenMP directives are issued in the form of the following constructs:
#pragma omp <_> [[(,)][[(,)]] …]. In our case, we do not use any options, and the parallel directive means that the code snippet following it, marked with curly brackets, refers to a parallel region and must be executed not on one, but on the entire specified number of cores.
We received a program that runs on one main or master core (master core), and those fragments allocated by the parallel directive run on a given number of cores, including both the master and slave cores. In the resulting implementation, the same vector summation cycle will be executed immediately on 8 cores.
A typical structure for the organization of parallel computing in OpenMP is shown in Figure 1.

Figure 1. The principle of parallel computing in OpenMP
The execution of a program code always begins with a sequential region, executed on a single core in a leading thread. At the point of beginning of a parallel region, indicated by the corresponding OpenMP directive, the organization of parallel execution following the OpenMP directive of the code in the stream set (parallel region) occurs. The figure shows only four parallel streams for simplicity. At the end of a parallel region, the flows merge, waiting for each other’s work to finish, and then a successive region follows again.
So, we managed to use 8 cores for the implementation of our program, however, there is no sense in such parallelization, since all cores do the same work. 8 cores 8 times formed the same output data array. The processing time did not decrease. Obviously, it is necessary to somehow divide the work between different cores.
Let's draw an analogy. Let there be a team of 8 people. One of them is paramount; the rest are his assistants. They receive requests for various works. The main worker accepts and executes orders, connecting, whenever possible, his assistants. The first job that our employees took up was to translate text from English into Russian. The brigadier took up the work, took the source text, prepared the dictionaries, copied the text for each of his assistants and distributed to everyone the same text, without dividing the work between them. The translation will be completed. The task will be solved correctly. However, there will be no gain from having 7 helpers. Quite the contrary. If they have to share the same dictionary, or a computer, or a sheet with the source text, the task execution time may be delayed. OpenMP also works in our first example. Requires separation of work. Each employee should indicate which fragment of the general text he should translate.
An obvious way to divide work between kernels in the context of the task of summing arrays is to distribute loop iterations among the cores depending on the core number. It is enough to find out inside which parallel code the code is running inside the parallel region, and specify a range of loop iterations depending on this number:
#include <ti/omp/omp.h> void vecsum (float * x, float * y, float * z, int N) { omp_set_num_threads(8); #pragma omp parallel { core_num = omp_get_thread_num(); a=(N/8)*core_num; b=a+N/8; for (int i=a; i<b; i++) z[i] = x[i] + y[i]; } } The kernel number is read by the OpenMP function omp_get_thread_num () ;. This function, being inside a parallel region, runs the same on all cores, but on different cores gives a different result. Due to this, it becomes possible to further divide the work within the parallel region. For simplicity, we assume that the number of iterations of the cycle N is a multiple of the number of kernels. The reading of the core number can be hardware based on the presence in each core of a special register core number - the DNUM register on TMS320C6678 processors. It can be accessed by various means, including assembler commands or CSL support library functions. However, you can use the functionality provided by the OpenMP add-in. Here, however, we must again pay attention to the fact that the kernel number and the number of the parallel OpenMP region are different concepts. For example, the 3rd parallel thread may well run on, say, the 5th core. Moreover, in the next parallel region or with the repetition of the same parallel region, the 3rd stream can already be executed on, for example, the 4th core. And so on.
We got a program running on 8 cores. Each core processes its part of the input arrays and forms the corresponding area of the output array. Each of our employees translates their 1/8 part of the text and, ideally, we get an 8-fold acceleration of the solution of the problem.
For and parallel for directives
We looked at the simplest parallel directive, which allows to extract fragments in code that should be executed on several cores in parallel. This directive, however, implies that all cores execute the same code and no work separation is provided for. We had to do it on our own, which looks a bit confusing.
Automatic indication of how work within a parallel region is divided between the cores is possible using the additional for directive. This directive is used inside a parallel region immediately before loops such as for and says that loop iterations should be distributed between the cores. The parallel and for directives can be used separately:
#pragma omp parallel #pragma omp for And can be used together in a single directive to reduce the record:
#pragma omp parallel for The use of the parallel for directive in our example of adding arrays leads to the following program code:
#include <ti/omp/omp.h> void vecsum (float * x, float * y, float * z, int N) { int i; omp_set_num_threads(8); #pragma omp parallel for for (i=0; i<N; i++) z[i] = x[i] + y[i]; } If we compare this program with the original single-core implementation, we will see that the differences are minimal. We just connected the header file omp.h, set the number of parallel threads and added one line - the parallel for directive.
Remark 1. Another difference that we deliberately hide in our reasoning is the transfer of the declaration of the variable i from the loop to the section describing the variables of the function, or rather from the parallel to the sequential region of the code. It is still too early to explain this action, however, it is crucial and will be explained later in the section on private and shared options.
Remark 2. We say that the iterations of the cycle are divided between the cores, however, we do not say how exactly they are divided. What are exactly loop iterations, which of the cores will be executed? OpenMP has the ability to set the rules for the distribution of iterations across parallel threads, and we will look at these features later. However, it is possible to precisely link a specific core to specific iterations only manually by the method discussed earlier. The truth is usually such a binding is not necessary. If the number of loop iterations is not a multiple of the number of cores, the distribution of iterations over the cores will be made so that the load is distributed as evenly as possible.
Directives sections and parallel sections
Work sharing between cores can be done either on the basis of data sharing, or on the basis of task sharing. Recall our analogy. If all workers do the same thing - they are engaged in translating text - but each translates a different piece of text, then this refers to the first type of work sharing - data separation. If workers perform various actions, for example, one translates the entire text, another searches for words in the dictionary, a third types the translation, and so on, then this refers to the second type of work division - task separation. The parallel and for directives we considered allowed us to separate the work by dividing the data. The separation of tasks between the cores allows you to execute the sections directive, which, as in the case of the for directive, can be used independently of the parallel directive or in conjunction with it to shorten the record:
#pragma omp parallel #pragma omp sections and
#pragma omp parallel sections As an example, we present a program that uses 3 processor cores, and each of the cores performs its own algorithm for processing the input signal x:
#include <ti/omp/omp.h> void sect_example (float* x) { omp_set_num_threads(3); #pragma omp parallel sections { #pragma omp section Algorithm1(x); #pragma omp section Algorithm2(x); #pragma omp section Algorithm3(x); } } Options shared, private and default
We choose to consider a new example. Let us turn to the calculation of the scalar product of two vectors. A simple C program that implements this procedure may look like this:
float x[N]; float y[N]; void dotp (void) { int i; float sum; sum = 0; for (i=0; i<N; i++) sum = sum + x[i]*y[i]; } The result of the execution (for test arrays of 16 elements) turned out to be equal to:
[TMS320C66x_0] sum = 331.0 Let us turn to the parallel implementation of this program, using the parallel for directive:
float x[N]; float y[N]; void dotp (void) { int i; float sum; sum = 0; #pragmaomp parallel for { for (i=0; i<N; i++) sum = sum + x[i]*y[i]; } } Result of performance:
[TMS320C66x_0] sum= 6.0 The program gives the wrong result! Why?
To answer this question, it is necessary to understand how the values of variables in the serial and parallel regions are related. We describe the logic of OpenMP in more detail.
The dotp () function starts to run as a sequential region on the 0th processor core. At the same time, in the memory of the processor, arrays x and y are organized, as well as variables I and sum. When the parallel directive is reached, the OpenMP utility functions come into play and organize the subsequent parallel operation of the kernels. There is an initialization of the cores, their synchronization, data preparation and a general start. What happens to variables and arrays?
All objects in OpenMP (variables and arrays) can be divided into common (shared) and private (private). Shared objects are located in shared memory and are used equally by all cores within a parallel region. Common objects coincide with objects of the same name in a sequential region. They move from sequential to parallel region and back unchanged, while maintaining their value. Access to such objects within a parallel region is equal for all cores, and there may be conflicts of general access. In our example, the x and y arrays, as well as the variable sum, turned out to be common by default. It turns out that all cores use the same variable sum as a battery. As a result, sometimes a situation arises in which several cores simultaneously read the same current value of the battery, add their partial contribution to it and write a new value to the battery. In this case, the core that records last, erases the work of the other cores. It is for this reason that our example gave the wrong result.
The principle of working with public and private variables is illustrated in Figure 2.

Figure 2. Illustration of OpenMP operation with public and private variables
Private objects are copies of the original objects, created separately for each kernel. These copies are created dynamically when initializing a parallel region. In our example, the variable i as a loop iteration count is considered private by default. When the parallel directive is reached, 8 copies (by the number of parallel threads) of this variable are created in the processor's memory. Private variables are located in the private memory of each kernel (they can be located in local memory, or they can also be shared, depending on how we declared them and configured the memory). Private copies by default are not related to the source objects of the sequential region. By default, the values of the source objects are not transferred to the parallel region. What private copies of objects are at the beginning of a parallel region is unknown. At the end of a parallel region, the values of private copies are simply lost, unless special measures are taken to transfer these values to a sequential region, which we will discuss later.
To explicitly tell the compiler which objects should be considered private and which should be shared, the options shared and private are used in conjunction with the OpenMP directives. The list of objects belonging to the public or private is indicated by a comma in brackets after the corresponding option. In our case, the variables i and sum should be private, and the arrays x and y should be common. Therefore, we will use the construction of the form:
#pragma omp parallel for private(i, sum) shared(x, y) when opening a parallel region. Now each core will have its own battery, and accumulations will go independently of each other. Additionally, the batteries must now be reset, since their initial value is unknown. In addition, the question arises how to combine the particular results obtained on each of the nuclei. One option is to use a special common array of 8 cells, in which each core will place its result inside a parallel region, and after leaving the parallel region, the main core summarizes the elements of this array and forms the final result. We get the following program code:
float x[N]; float y[N]; float z[8]; void dotp (void) { int i, core_num; float sum; sum = 0; #pragma omp parallel private(i, sum, core_num) shared(x, y, z) { core_num = omp_get_thread_num(); sum = 0; #pragma omp for for (i=0; i<N; i++) sum = sum + x[i]*y[i]; z[core_num] = sum; } for (i=0; i<8; i++) sum = sum + z[i]; } Result of performance:
[TMS320C66x_0] sum= 331.0 The program works correctly, although it is a bit cumbersome. We will discuss further how to simplify it.
It is interesting that when specifying the names of OpenMP arrays as private objects during initialization of a parallel region, it acts the same way as with variables — it dynamically creates private copies of these arrays. You can verify this by conducting a simple experiment: declaring an array through the private option, print the values of the pointers to this array in the sequential and parallel regions. We will see 9 different addresses (with the number of cores - 8).
Next, you can make sure that the values of the elements of the arrays are not related to each other. In addition, when you later enter the same parallel region, the addresses of private copies of the arrays may be different, and the default values of the elements are not saved. All this leads us to the fact that OpenMP directives that open and close a parallel region can be quite cumbersome and require a specific execution time.
If there is no explicit indication of its type (common / private) for an object in the opening directive of a parallel region, then OpenMP “acts” according to certain rules described in [5]. Undefined objects OpenMP refers to the default type. What type it will be, private or shared, is determined by the environment variable — one of the OpenMP operation parameters. . , . . for parallel for, .
default. , – . , none, , , , :
#pragma omp parallel private(sum, core_num) shared(x, y, z) default(i) or:
#pragma omp parallel private(i, sum, core_num) shared(x, y, z) default(none) reduction
In the considered example of the implementation of the scalar product on 8 cores, we noted one drawback: combining the private results of the cores requires significant code modifications, which makes it cumbersome and inconvenient. At the same time, the openMP concept implies maximum transparency in the transition from single-core to multi-core implementation and vice versa. Simplify the program discussed in the previous section, allows the use of the reduction option.
The reduction option allows the compiler to indicate that the results of the kernels should be combined, and sets the rules for such a combination. The reduction option is provided for a number of the most common situations. The option syntax is as follows:
reduction ( : ) – , . , .
– , .
reduction, OpenMP , 1.
: +, *, -, &, |, ^, &&, ||, max, min
: 0, 1, 0, 0, 0, 0, 1, 0, , .
reduction c «+» sum:
float x[N]; float y[N]; void dotp (void) { int i; float sum; #pragma omp parallel for private(i) shared(x, y) reduction(+:sum) for (i=0; i<N; i++) sum += x[i]*y[i]; } Result of performance:
[TMS320C66x_0] sum= 331.0 «» !
OpenMP
, , . , , . , , . , . .
, , ( ) , . , , . , ( ), , . -: , , . , OpenMP- , . , , - - () .
In OpenMP, two types of synchronization can be distinguished: implicit and explicit. Implicit synchronization occurs automatically at the end of parallel regions, as well as at the end of a number of directives that can be applied within parallel regions, including omp for, omp sections, and so on. This automatically synchronizes the cache.
If the problem solving algorithm requires synchronizing the kernels in those points of the program inside a parallel region where automatic synchronization is not provided, the developer can use explicit synchronization — tell the OpenMP compiler explicitly using special directives that synchronization is required at this point. Consider the main of these guidelines.
Barrier directive
The barrier directive is written as:
#pragma omp barrier and explicitly sets the synchronization point for parallel OpenMP threads within a parallel region. Let's give the following example of using the directive:
#define CORE_NUM 8 float z[CORE_NUM]; void arr_proc(void) { omp_set_num_threads(CORE_NUM); int i, core_num; float sum; #pragma omp parallel private(core_num, i, sum) { core_num=omp_get_thread_num(); z[core_num]=core_num; #pragma omp barrier sum = 0; for(i=0;i<CORE_NUM;i++) sum=sum+z[i]; #pragma omp barrier z[core_num]=sum; } for(i=0;i<CORE_NUM;i++) printf("z[%d] = %f\n", i, z[i]); } . z, z, z. z, . : . z, . . barrier . z . , , , . , z, , . barrier z. – .
Critical directive
The critical directive is written as:
#pragma omp critical [ ] And selects a code fragment inside a parallel region, which can be executed at a time by only one core.
, . . , , , , . , . , . , , : , , ; .
. , , critical. :
#define CORE_NUM 8 #define N 1000 #define M 80 void crit_ex(void) { int i, j; int A[N]; int Z[N] = {0}; omp_set_num_threads(CORE_NUM); #pragma omp parallel for private (A) for (i = 0; i < M; i++) { poc_A(A, N); #pragma omp critical for (j=0; j<N; j++) Z[j] = Z[j] + A[j]; } } () Z. 8 . , . , . Z. , . , . , ( ), , . . , .
Let's replace the critical section in our code with the following construction.
#pragma omp critical (Z1add) for (j=0; j<N; j++) Z1[j] = Z1[j] + A[j]; #pragma omp critical (Z2mult) for (j=0; j<N; j++) Z2[j] = Z2[j] * A[j]; Now we have two critical sections. In one, the results of the work of the nuclei are combined by summation; in the other, by multiplication. Both sections can run simultaneously on only one core, however, different sections can run simultaneously on different cores. If you enter the name of a region into the construction of the directive critical, then the kernel will be denied access to the code only if another core works in this particular region. If the names of the regions are not assigned, then the kernel will not be able to enter any of the critical regions if the other core works with any of them, even if they are not related to each other.
Atomic directive
The atomic directive is written as:
#pragma omp atomic [read | write | update | capture] In the previous example, different kernels were forbidden to execute code from the same region at the same time. However, this may not seem rational on closer examination. After all, access conflicts to a shared resource consist in the fact that different cores can simultaneously access the same memory cells. If, within the same code, the call goes to different memory cells, the result will not be distorted. The atomic directive allows the synchronization of cores to memory elements. It indicates that in the next line of the memory operation is atomic - inseparable: if some core starts operation with a certain memory cell, access to this memory cell will be closed for all other cores until the first core finishes working with her. At the same time, the atomic directive is accompanied by options indicatingWhat type of operation is performed with memory: read / write / modify / capture. The above example when applying the atomic directive will look like this.
#define CORE_NUM 8 #define N 1000 #define M 80 void crit_ex(void) { int i, j; int A[N]; int Z[N] = {0}; omp_set_num_threads(CORE_NUM); #pragma omp parallel for private (A) for (i = 0; i < M; i++) { poc_A(A, N); for (j=0; j<N; j++) { #pragma omp atomic update Z[j] = Z[j] + A[j]; } } , atomic , , . . , , atomic , , , . , critical MxT1 , – , T1 – ; atomic 2 . atomic , 2 , 1.
OpenMP – (/++), , , . 8- TMS320C6678 Texas Instruments. OpenMP – . , , OpenMP, . . OpenMP . .
, , OpenMP , . , , .
, OpenMP . OpenMP OpenMP . OpenMP 1 2, Texas Instruments TMS320C6678 . . OpenMP; , ; OpenMP; .
Literature
1. G. Blake, RG Dreslinski, T. Mudge, «A survey of multicore processors,» Signal Processing Magazine, vol. 26, no. 6, pp. 26-37, Nov. 2009.
2. LJ Karam, I. AlKamal, A. Gatherer, GA Frantz, «Trends in multicore DSP platforms,» Signal Processing Magazine, vol. 26, no. 6, pp. 38-49, 2009.
3. A. Jain, R. Shankar. Software Decomposition for Multicore Architectures, Dept. of Computer Science and Engineering, Florida Atlantic University, Boca Raton, FL, 33431.
4. Web- OpenMP Architecture Review Board (ARB): openmp.org .
5. OpenMP Application Programming Interface. Version 4.5 November 2015. OpenMP Architecture Review Board. P. 368.
6. OpenMP 4.5 API C/C++ Syntax Reference Guide. OpenMP Architecture Review Board. 2015.
7. J. Diaz, C. Muñoz-Caro, A. Niño. A Survey of Parallel Programming Models and Tools in the Multi and Many-Core Era. IEEE Transactions on Parallel and Distributed Systems. – 2012. – Vol. 23, Is. 8, pp. 1369 – 1386.
8. A. Cilardo, L. Gallo, A. Mazzeo, N. Mazzocca. Efficient and scalable OpenMP-based system-level design. Design, Automation & Test in Europe Conference & Exhibition (DATE). – 2013, pp. 988 – 991.
9. M. Chavarrías, F. Pescador, M. Garrido, A. Sanchez, C. Sanz. Design of multicore HEVC decoders using actor-based dataflow models and OpenMP. IEEE Transactions on Consumer Electronics. – 2016. – Vol. 62. – Is. 3, pp. 325 – 333.
10. M. Sever, E. Çavus. Parallelizing LDPC Decoding Using OpenMP on Multicore Digital Signal Processors. 45th International Conference on Parallel Processing Workshops (ICPPW). – 2016, pp. 46 – 51.
11. A. Kharin, S. Vityazev, V. Vityazev, N. Dahnoun. Parallel FFT implementation on TMS320c66x multicore DSP. 6th European Embedded Design in Education and Research Conference (EDERC). – 2014, pp. 46 – 49.
12. D. Wang, M. Ali, ―Synthetic Aperture Radar on Low Power Multi-Core Digital Signal Processor,‖ High Performance Extreme Computing (HPEC), IEEE Conference on, pp. 1 – 6, 2012.
13. . . , . . . - . ., 2007, 138 .
14. . . . . . , 2006, 90 .
15. .. . OpenMP. . 2009 , 78 .
16. .. . OpenMP. .: 2012, 121 .
17. TMS320C6678 Multicore Fixed and Floating-Point Digital Signal Processor, Datasheet, SPRS691E, Texas Instruments, p. 248, 2014.
2. LJ Karam, I. AlKamal, A. Gatherer, GA Frantz, «Trends in multicore DSP platforms,» Signal Processing Magazine, vol. 26, no. 6, pp. 38-49, 2009.
3. A. Jain, R. Shankar. Software Decomposition for Multicore Architectures, Dept. of Computer Science and Engineering, Florida Atlantic University, Boca Raton, FL, 33431.
4. Web- OpenMP Architecture Review Board (ARB): openmp.org .
5. OpenMP Application Programming Interface. Version 4.5 November 2015. OpenMP Architecture Review Board. P. 368.
6. OpenMP 4.5 API C/C++ Syntax Reference Guide. OpenMP Architecture Review Board. 2015.
7. J. Diaz, C. Muñoz-Caro, A. Niño. A Survey of Parallel Programming Models and Tools in the Multi and Many-Core Era. IEEE Transactions on Parallel and Distributed Systems. – 2012. – Vol. 23, Is. 8, pp. 1369 – 1386.
8. A. Cilardo, L. Gallo, A. Mazzeo, N. Mazzocca. Efficient and scalable OpenMP-based system-level design. Design, Automation & Test in Europe Conference & Exhibition (DATE). – 2013, pp. 988 – 991.
9. M. Chavarrías, F. Pescador, M. Garrido, A. Sanchez, C. Sanz. Design of multicore HEVC decoders using actor-based dataflow models and OpenMP. IEEE Transactions on Consumer Electronics. – 2016. – Vol. 62. – Is. 3, pp. 325 – 333.
10. M. Sever, E. Çavus. Parallelizing LDPC Decoding Using OpenMP on Multicore Digital Signal Processors. 45th International Conference on Parallel Processing Workshops (ICPPW). – 2016, pp. 46 – 51.
11. A. Kharin, S. Vityazev, V. Vityazev, N. Dahnoun. Parallel FFT implementation on TMS320c66x multicore DSP. 6th European Embedded Design in Education and Research Conference (EDERC). – 2014, pp. 46 – 49.
12. D. Wang, M. Ali, ―Synthetic Aperture Radar on Low Power Multi-Core Digital Signal Processor,‖ High Performance Extreme Computing (HPEC), IEEE Conference on, pp. 1 – 6, 2012.
13. . . , . . . - . ., 2007, 138 .
14. . . . . . , 2006, 90 .
15. .. . OpenMP. . 2009 , 78 .
16. .. . OpenMP. .: 2012, 121 .
17. TMS320C6678 Multicore Fixed and Floating-Point Digital Signal Processor, Datasheet, SPRS691E, Texas Instruments, p. 248, 2014.
Source: https://habr.com/ru/post/318762/
All Articles