Analysis of the statistical language model from Google - part 1: vector representation of characters
This year, Google Brain researchers published an article called Exploring the Limits of Language Modeling , which described a language model that significantly reduced perplexion (from about 50 to 30) in the One Billion Word Benchmark dictionary.
In this post we will tell about the lowest level of this model - the representation of characters.

To begin with, we define the very concept of a language model . The language model is a probability distribution on a set of vocabulary sequences. For a sentence like “Hello world” or “Buffalo buffalo Buffalo buffalo buffalo buffalo Buffalo buffalo”, the language model gives us the likelihood that we will meet this sentence.
')
The quality model of the language model is perplexity — a measure of how well a model predicts the details of a test collection (the less perplexion, the better the model).
The
("<S>" and "</ S>" denote the beginning and end of a sentence).

This is the abbreviation of the character-level convolutional neural network. If you do not know what it is, forget what I just said, since in this post we will focus on what happens when the network starts performing any convolutions, namely, on character embedding .
The most obvious way to represent a symbol as an input value for our neural network is direct coding ( one-hot encoding ). For example, an alphabet consisting of lowercase Latin letters would be represented as follows:
And so on. Instead, we learn the “dense” representation of each character. If you have already used a vector representation of words like word2vec , then this method will seem familiar to you.
The first CNN Char layer is responsible for translating the raw characters of the input word to a vector representation, which is passed to the input to convolution filters.
In
It is quite difficult to comprehend. Let's reduce the dimensionality of the representation of characters to two using the t-SNE algorithm to represent where they will be located relative to each other. t-SNE will position our view so that the pairs with the smallest distance in the 16-dimensional vector space will also be closer to each other in a two-dimensional projection.

t-SNE representation of the most frequency symbols. Pink marks correspond to special meta-characters. <S> and </ S> mark the beginning and end of a sentence. <W> and </ W> mark the beginning and end of a word. <PAD> uses 50-character word length restrictions. Yellow marks are punctuation marks, blue marks are numbers, and light and dark green marks are upper and lower case letter symbols.
Here are some interesting patterns:
Also worth noting is the lack of pattern . In addition to not too regular matching pairs of lowercase / uppercase, otherwise the arrangement of letters seems random. They are quite distant from each other and spread over the entire projection plane. Not observed, for example, islands of vowels or sonorous consonants. There is no universal separation of lowercase letters from capital letters.
Perhaps this information is reflected in the view, but t-SNE simply does not have enough degrees of freedom to reflect these differences in a two-dimensional projection. Maybe by examining each dimension in turn, we could get more information?

Or maybe not. You can look at the graphs of all 16 measurements here - I did not manage to find any patterns in them.
Perhaps the most famous feature of the vector representations of words is the ability to add and subtract them and (sometimes) get semantically meaningful results. For example,
I wonder if we can do the same with the representation of characters. There are not too many obvious analogies here, but what about adding and subtracting “title”?
'a' refers to 'A' just as 'b' refers to ...
Okay, not a good start. Let's try again:
Partial success?
Having made many attempts, we now and then received the correct answer, but how is this method better than random? Do not forget that half of the lowercase letters are located in close proximity to the corresponding capital letters. Already therefore, if we move from a letter in a random direction, we are very likely to stumble upon its pair.
I think it remains to try only one thing:
Note for the future: never use character embedding to calculate tips.
It seems useful to place figures close in size close to each other due to interchangeability. A “36-year-old” can easily be replaced with a “37-year-old” (or even a “26-year-old”), 800 bucks are more like 900 or 700 bucks than 100. Looking at our t-SNE projection, we can say that This model works. But this does not mean that the numbers are lined up (let's start at least with the fact that models need to learn some of the subtleties associated with the numbers, for example, take into account that the year most often begins with “19” or “20”.
Before guessing why a certain character is presented in one way or another, it is worth asking: why use character embedding at all?
One of the reasons may be a decrease in the complexity of the model. For each character, it will be enough for the selection filter of attributes in Char CNN to remember 16 weights instead of 256. If we remove the vector representation layer, the number of weights at the feature selection stage will increase by 16 times, that is, from about 460K (4096 filters * maximum width 7 * 16- dimensional representation) to 7.3M. It seems like a lot, but the total number of parameters for the entire network (CNN + LSTM + Softmax) is 1.04 billion! So a couple extra millions will not play a big role.
In fact,
Apparently, the best performance meant a lower perplexion, and not a model learning speed, for example.
Why does character representation improve performance? Well, why does the word presentation improve the performance of tasks in the field of natural languages? They improve the generalization . There are many words in a language, and many of them are rare . If you meet the words “raspberry”, “strawberry” and “gooseberry” in the same context, we assign them close vectors. And if we have repeatedly met the phrase "raspberry jam" and "strawberry jam", we can assume that the combination of "gooseberry jam" is quite likely, even if we have never met him in our case.
To begin with, the analogy with the word vectors is not quite appropriate here. The Billion Word package consists of 800,000 individual words, while we are dealing with only 256 characters. Is it worth thinking about generalization? And how to generalize, for example, 'g' to another character?
It seems the answer will be “no way”. Sometimes we can draw conclusions on the basis of generalization for upper and lower case versions of a single letter, but in general, alphabetic characters are isolated, and they are all found so often that we should not be bothered by generalization.
But are there any characters that are rarely enough for generalization to play an important role? Let's get a look.

The frequency of the n-th most popular symbol. Calculated on the basis of the Billion Word Benchmark training set (about 770 thousand words). More than 50 characters are completely absent in the package (for example, ASCII control characters).
Yes, this is not quite Zipf’s law (we are approaching a straight line using only a logarithmic scale on the y axis instead of a double logarithmic scale), but it’s still clear that there are a large number of rarely used symbols (mostly non-ASCII characters and rare punctuation marks ).
Perhaps our vector representation helps us use generalization to infer such symbols. On the t-SNE chart above, I depicted only those symbols that are quite common (I took the least frequency letter symbol 'x' for the lower border). What if we depict a representation for characters appearing at least 50 times in the body?
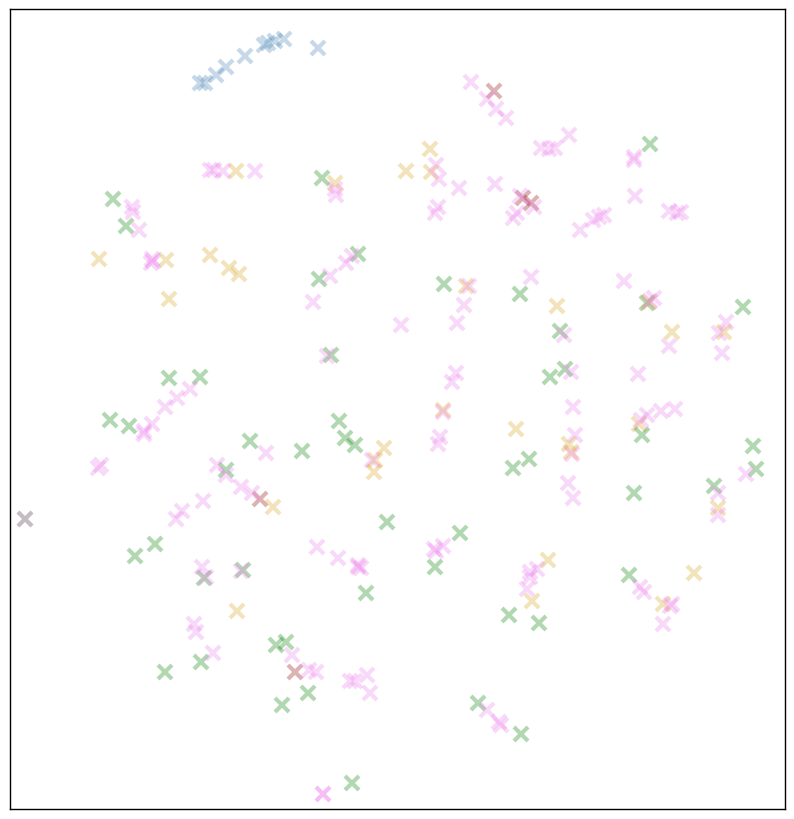
Green = letters, blue = numbers, yellow = punctuation, red-brown = metacharacters. The pink marks are bytes up to 127 and everything else that is not included in the previous groups.
This seems to confirm our hypothesis! Letters, as before, are antisocial and rarely touch each other. But in several areas, our rare “pink” characters form dense clusters or lines.
The most likely assumption: the alphabetic characters stand apart, while rare symbols, as well as symbols with a high degree of interchangeability (numbers, punctuation marks at the end of a sentence) tend to be located close to each other.
That's all for now. Thanks to the Google Brain team for the release of
Next time we will look at the second stage of the CNN Char - convolutional filters.
In this post we will tell about the lowest level of this model - the representation of characters.

Introduction: Language Models
To begin with, we define the very concept of a language model . The language model is a probability distribution on a set of vocabulary sequences. For a sentence like “Hello world” or “Buffalo buffalo Buffalo buffalo buffalo buffalo Buffalo buffalo”, the language model gives us the likelihood that we will meet this sentence.
')
The quality model of the language model is perplexity — a measure of how well a model predicts the details of a test collection (the less perplexion, the better the model).
The
lm_1b language model takes one word from a sentence and calculates the probability distribution of the next word. Thus, it can calculate the probability of a sentence such as “Hello, world”, as follows: P("<S> Hello world . </S>") = product(P("<S>"), P("Hello" | "<S>"), P("world" | "<S> Hello"), P("." | "<S> Hello world"), P("</S>" | "<S> Hello world .")) ("<S>" and "</ S>" denote the beginning and end of a sentence).
Lm_1b architecture
lm_1b consists of three main components (see figure):
- A CNN char (blue rectangle) receives the characters that make up a word as input, displays a word vector representation (word embedding).
- LSTM (Long short-term memory) (yellow) gets a representation of the word, as well as a state vector (for example, words that have already been encountered in this sentence) and computes the representation of the next word.
- The last layer, softmax (green), taking into account the information received from the LSTM, calculates the distribution for all vocabulary words.
Char CNN
This is the abbreviation of the character-level convolutional neural network. If you do not know what it is, forget what I just said, since in this post we will focus on what happens when the network starts performing any convolutions, namely, on character embedding .
Character Embedding
The most obvious way to represent a symbol as an input value for our neural network is direct coding ( one-hot encoding ). For example, an alphabet consisting of lowercase Latin letters would be represented as follows:
onehot('a') = [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0] onehot('c') = [0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0] And so on. Instead, we learn the “dense” representation of each character. If you have already used a vector representation of words like word2vec , then this method will seem familiar to you.
The first CNN Char layer is responsible for translating the raw characters of the input word to a vector representation, which is passed to the input to convolution filters.
In
lm_1b alphabet has a dimension of 256 (non-ASCII characters are expanded to several bytes, each of which is encoded separately) and is mapped to a dimension space of 16. For example, the character 'a' is represented by the following vector: array([ 1.10141766, -0.67602301, 0.69620615, 1.96468627, 0.84881932, 0.88931531, -1.02173674, 0.72357982, -0.56537604, 0.09024946, -1.30529296, -0.76146501, -0.30620322, 0.54770935, -0.74167275, 1.02123129], dtype=float32) It is quite difficult to comprehend. Let's reduce the dimensionality of the representation of characters to two using the t-SNE algorithm to represent where they will be located relative to each other. t-SNE will position our view so that the pairs with the smallest distance in the 16-dimensional vector space will also be closer to each other in a two-dimensional projection.

t-SNE representation of the most frequency symbols. Pink marks correspond to special meta-characters. <S> and </ S> mark the beginning and end of a sentence. <W> and </ W> mark the beginning and end of a word. <PAD> uses 50-character word length restrictions. Yellow marks are punctuation marks, blue marks are numbers, and light and dark green marks are upper and lower case letter symbols.
Here are some interesting patterns:
- The numbers are not only grouped together, but they are arranged in order and “snake”.
- In most cases, the same upper and lower case letters are located side by side, but some (for example, k / K) are significantly distant from each other.
- In the upper right corner there are punctuation marks that can complete a sentence (
.?!). - Metacharacters (pink) form a so-called loose cluster, and the other special characters make it even more loose (with '%' and ')' as drop-down values).
Also worth noting is the lack of pattern . In addition to not too regular matching pairs of lowercase / uppercase, otherwise the arrangement of letters seems random. They are quite distant from each other and spread over the entire projection plane. Not observed, for example, islands of vowels or sonorous consonants. There is no universal separation of lowercase letters from capital letters.
Perhaps this information is reflected in the view, but t-SNE simply does not have enough degrees of freedom to reflect these differences in a two-dimensional projection. Maybe by examining each dimension in turn, we could get more information?

Or maybe not. You can look at the graphs of all 16 measurements here - I did not manage to find any patterns in them.
Vector computing
Perhaps the most famous feature of the vector representations of words is the ability to add and subtract them and (sometimes) get semantically meaningful results. For example,
vec('woman') + (vec('king') - vec('man')) ~= vec('queen') I wonder if we can do the same with the representation of characters. There are not too many obvious analogies here, but what about adding and subtracting “title”?
def analogy(a, b, c): """a is to b, as c is to ___, Return the three nearest neighbors of c + (ba) and their distances. """ # ... 'a' refers to 'A' just as 'b' refers to ...
>>> analogy('a', 'A', 'b') b: 4.2 V: 4.2 Y: 5.1 Okay, not a good start. Let's try again:
>>> analogy('b', 'B', 'c') c: 4.2 C: 5.2 +: 5.9 >>> analogy('b', 'B', 'd') D: 4.2 ,: 4.9 d: 5.0 >>> analogy('b', 'B', 'e') N: 4.7 ,: 4.7 e: 5.0 Partial success?
Having made many attempts, we now and then received the correct answer, but how is this method better than random? Do not forget that half of the lowercase letters are located in close proximity to the corresponding capital letters. Already therefore, if we move from a letter in a random direction, we are very likely to stumble upon its pair.
Vector computing (now for real)
I think it remains to try only one thing:
>>> analogy('1', '2', '2') 2: 2.4 E: 3.6 3: 3.6 >>> analogy('3', '4', '8') 8: 1.8 7: 2.2 6: 2.3 >>> analogy('2', '5', '5') 5: 2.7 6: 4.0 7: 4.0 # It'd be really surprising if this worked... >>> nearest_neighbors(vec('2') + vec('2') + vec('2')) 2: 6.0 1: 6.9 3: 7.1 Note for the future: never use character embedding to calculate tips.
It seems useful to place figures close in size close to each other due to interchangeability. A “36-year-old” can easily be replaced with a “37-year-old” (or even a “26-year-old”), 800 bucks are more like 900 or 700 bucks than 100. Looking at our t-SNE projection, we can say that This model works. But this does not mean that the numbers are lined up (let's start at least with the fact that models need to learn some of the subtleties associated with the numbers, for example, take into account that the year most often begins with “19” or “20”.
Why all this?
Before guessing why a certain character is presented in one way or another, it is worth asking: why use character embedding at all?
One of the reasons may be a decrease in the complexity of the model. For each character, it will be enough for the selection filter of attributes in Char CNN to remember 16 weights instead of 256. If we remove the vector representation layer, the number of weights at the feature selection stage will increase by 16 times, that is, from about 460K (4096 filters * maximum width 7 * 16- dimensional representation) to 7.3M. It seems like a lot, but the total number of parameters for the entire network (CNN + LSTM + Softmax) is 1.04 billion! So a couple extra millions will not play a big role.
In fact,
lm_1b includes char embedding, because their CNN char is developed based on the article by Kim et. al 2015, where char embedding was also used. The footnote in this article explains:Since | C | usually a little, some authors use direct coding for the vector representation of characters. However, we found that using the representation of symbols of smaller dimensions shows slightly better performance.
Apparently, the best performance meant a lower perplexion, and not a model learning speed, for example.
Why does character representation improve performance? Well, why does the word presentation improve the performance of tasks in the field of natural languages? They improve the generalization . There are many words in a language, and many of them are rare . If you meet the words “raspberry”, “strawberry” and “gooseberry” in the same context, we assign them close vectors. And if we have repeatedly met the phrase "raspberry jam" and "strawberry jam", we can assume that the combination of "gooseberry jam" is quite likely, even if we have never met him in our case.
Generalization of characters?
To begin with, the analogy with the word vectors is not quite appropriate here. The Billion Word package consists of 800,000 individual words, while we are dealing with only 256 characters. Is it worth thinking about generalization? And how to generalize, for example, 'g' to another character?
It seems the answer will be “no way”. Sometimes we can draw conclusions on the basis of generalization for upper and lower case versions of a single letter, but in general, alphabetic characters are isolated, and they are all found so often that we should not be bothered by generalization.
But are there any characters that are rarely enough for generalization to play an important role? Let's get a look.

The frequency of the n-th most popular symbol. Calculated on the basis of the Billion Word Benchmark training set (about 770 thousand words). More than 50 characters are completely absent in the package (for example, ASCII control characters).
Yes, this is not quite Zipf’s law (we are approaching a straight line using only a logarithmic scale on the y axis instead of a double logarithmic scale), but it’s still clear that there are a large number of rarely used symbols (mostly non-ASCII characters and rare punctuation marks ).
Perhaps our vector representation helps us use generalization to infer such symbols. On the t-SNE chart above, I depicted only those symbols that are quite common (I took the least frequency letter symbol 'x' for the lower border). What if we depict a representation for characters appearing at least 50 times in the body?

Green = letters, blue = numbers, yellow = punctuation, red-brown = metacharacters. The pink marks are bytes up to 127 and everything else that is not included in the previous groups.
This seems to confirm our hypothesis! Letters, as before, are antisocial and rarely touch each other. But in several areas, our rare “pink” characters form dense clusters or lines.
The most likely assumption: the alphabetic characters stand apart, while rare symbols, as well as symbols with a high degree of interchangeability (numbers, punctuation marks at the end of a sentence) tend to be located close to each other.
That's all for now. Thanks to the Google Brain team for the release of
lm_1b . If you want to conduct your experiments with this model, do not forget to read the instructions here . I laid out the scripts with which I did the visualization for this post here - feel free to reuse or change them, although they look awful.Next time we will look at the second stage of the CNN Char - convolutional filters.
Oh, and come to work with us? :)wunderfund.io is a young foundation that deals with high-frequency algorithmic trading . High-frequency trading is a continuous competition of the best programmers and mathematicians of the whole world. By joining us, you will become part of this fascinating fight.
We offer interesting and challenging data analysis and low latency tasks for enthusiastic researchers and programmers. Flexible schedule and no bureaucracy, decisions are quickly made and implemented.
Join our team: wunderfund.io
Source: https://habr.com/ru/post/318454/
All Articles