10 new tales of lost time
Hi Habr! I decided to continue the series of articles on the Euler hypothesis, having written several improved versions of programs for solving a Diophantine equation of the form a 5 + b 5 + c 5 + d 5 = e 5 .
As you know, in order to solve any complex computational problem, you need to pay attention to at least the following points:
I paid the most attention to the first item. Let's see what came of it.
Immediately, I note that the code was written in C ++, the 32-bit MS Visual C ++ 2008 Compiler was compiled and started in one stream on the i5-2410M 2.3Ghz machine. It's just more convenient for me - to write code lying on a not very powerful laptop, and to set the 64-bit compiler too lazy. Measurements of time do not shine with accuracy, since the code was rarely run more than 1 time per measurement, while other processes like the browser could slightly affect the running time. However, for our purposes, the accuracy is acceptable.
')
And yet, with the filing of Dimchansky , I’ll clarify that I will look for integer solutions of the above equation for a, b, c, d, e> 0, of which exactly 2 pieces are known. There is a third solution, but there variables can take negative values. You can find them all here .
Let's start with the dumbest decision that can be. Code:
In fact, this is not the most stupid, because you can drive all the variables from 1 to n and at the end check that a <b <c <d <e. But then I would have had to wait too long. Working hours:
Pros: simple as a boot, spelled quickly, requires O (1) memory, finds the classic solution 27 5 + 84 5 + 110 5 + 133 5 = 144 5 .
Cons: it is inhibited .
Let's speed up our decision a bit. In fact, this option is equivalent to what was proposed by comrade drBasic .
Here we create an array, where we save the fifth powers of all numbers from 1 to n, then inside the four nested loops we use a binary search to check if there is a 5 + b 5 + c 5 + d 5 number in the array or not.
This option is already running faster, I even had the patience to wait for the end of the program for n = 1000.
Pros: still quite simple, faster than a stupid solution, it is easy to write, it finds a classic solution.
Cons: O (n) memory required, still slow .
In fact, it makes no sense to store all the degrees in an array and look for something binpoisk there. We already know what number in this array is at position i. You can simply run a bin-search on a “virtual” array. No sooner said than done:
Now the array is not needed, we have pure binary search.
Unfortunately, the execution time has sunk, probably due to the fact that inside bin search we re-calculate the fifth power every time. Well, okay.
Pros: requires O (1) memory, finds a classic solution.
Cons: slower than the previous decision.
Let's look at our equation again:
a 5 + b 5 + c 5 + d 5 = e 5
or, for simplicity, A = B.
Let the algorithm executes our 4 nested loops. Fix the values of a, b and c and see how the values of d and e behave. Let for some d = x the smallest value of e, for which A <= B, is equal to y. For d = x, it makes no sense to consider the values of e> y. Note also that for d = x + 1 the smallest value of e, for which A <= B, is not less than y. That is, we can always just gently increase the value of e while we go by d and this ensures that we do not miss anything. Since the values of d and e only increase, the total pass through them will take O (n). This idea is called the two-pointer method.
The code is less than for bin search, and there is more benefit.
Because of the large hidden constant, this solution starts to overtake solution # 2 by O (n 4 log n) only when n is about 500. It can, of course, be accelerated by calculating the fifth degrees more thoughtfully, but we will not do that.
Pros: asymptotically faster solution # 2, requires O (1) memory. Yes, it does.
Cons: far from the optimum, a large hidden constant.
Let's develop an idea with two pointers, and turn the rest of the decision upside down. Suppose we have the equation A + B = C, and for each of the A, B, C we have n (A), n (B), n (C) ways to choose them. Let's fix some value C, and sort all valid values for A and B by ascending order. Then we can run on the values of A and B with the help of two pointers and for O (n (A) + n (B)) check everything you need for the current value of C! Namely: for some fixed A we will decrease the value of B, while A + B> C. As soon as A + B <= C becomes, then there is no point in reducing B. Then we increase A and continue the process of decreasing B. The whole algorithm will take completely O (n (A) log n (A) + n (B) log n (B) + (n (A) + n (B)) n ( WITH) ).
For the case when A and B are elements of the same set, the algorithm for checking fixed C can be stopped as soon as the current A and B meet (since, without loss of generality, we can assume that A <B).
Now in our equation we denote (a 5 + b 5 ) for A, (c 5 + d 5 ) for B, and e 5 for C. And write the following code:
Since the pairs (a, b) (and (c, d)) are of the order of n 2 , the sorting will take O (n 2 log n), and the next check using pointers is O (n 3 ). Total clean cube.
Exercise . Find the logical error in the code above.
Significant acceleration allows you to drag n = 5000 for a reasonable time. Checks when adding pairs to an array are needed to avoid overflow.
Pros: probably the fastest asymptotic algorithm.
Cons: a large hidden constant, works only up to n of the order of 5000, eats even O (n 2 ) memory.
Suddenly. From the user's submission of erwins22 from this comment, we consider the residuals that we can get by dividing the fifth power by 11. That is, what a can be compared x 5 = a mod 11. It turns out that the possible values of a are 0, 1 and -1 (mod 11) (check for yourself and make sure).
Then, in the equality a 5 + b 5 + c 5 + d 5 = e 5 units and minus ones, the total even number (they must balance each other so that the parity converges), it follows that one of the numbers a, b, c, d, e is comparable from 0 to module 11, that is, divisible by 11. Let's put it separately in one direction, we get one of two options:
(a 5 + b 5 ) + (c 5 + d 5 ) = e 5 ; e = 0 mod 11
(e 5 - a 5 ) - (b 5 + c 5 ) = d 5 ; d = 0 mod 11
You will not believe, but if the number x is divisible by 11, then the number x 5 is divisible by 161051. Hence, the left-hand side of the above equalities must also be divisible by 161051. As you can see, in the equations above, some numbers are already carefully paired with brackets. Now, if we fix the first bracket, then the second bracket can have only one of all possible 161051 residues when divided by 161051. Thus, for each of O (n 2 ) first brackets, on average, there are O (n 2/161051) second. If we now sort out all of them and see if the result is an exact fifth degree (for example, a binoisk in an array of fifth degrees), then we will find all the solutions in O (n 4 log n / 161051). Code:
The working time of this solution:
From the table it can be seen that for n = 500 and n = 1000 this solution even overtakes the cubic one. But then the cubic solution still begins to overtake. Asymptotics she is - you can not fool her.
Pros: very powerful clipping.
Cons: a large asymptotic, it is not clear how to fasten this idea to a cubic solution.
Let us temporarily forget about the tricks with the modules (we will remember from later on a bit later!) And redo our cubic solution so that it can work correctly for n> 5000. To do this, we implement 128-bit integers.
The operations that needed to be added are addition and construction to the fifth degree. There is still a subtraction, in this solution it is not needed, but it will be needed later. So let it be. Since the 128-bit number is implemented as pair, there are already operations <,>, =, and they work exactly as we need.
At the very beginning we immediately set the size of the vector. It’s not that this is done for optimization, I’m still too lazy to uncover the 64-bit compiler, and only 2GB of memory is available on 32 bits. Now for n = 10,000 it takes about 1.2GB per vector. If you expand the vector via push_back, then at the very end it captures more than 2 GB during reallocation (to increase from the length N to 2 * N you need 3 * N intermediate memory).
You can see that now the program has slowed down almost exactly 2 times with respect to solution # 5, but we have conquered the new impregnable vertex n = 10,000!
Pros: now does not overflow for n> 5000.
Cons: running 2 times slower than the solution # 5, eats a lot of memory.
Recall again the remnants of division by 11. We have two equalities:
(a 5 + b 5 ) + (c 5 + d 5 ) = e 5 ; e = 0 mod 11
(e 5 - a 5 ) - (b 5 + c 5 ) = d 5 ; d = 0 mod 11
Recall that the fifth degree modulo 11 always have residues 0, 1, or -1. We remove the restrictions of the form a <b <c <d and allow numbers to arbitrarily move from one bracket to another. Then it is easy to show (by considering all cases) that they can always be moved so that each of the brackets will be equal to 0 modulo 11. Well, now we will need to go through all the pairs of numbers from 1 to n, find the sum and difference of their fifth degrees and remember only those that are divided by 11. And the remaining pairs can simply be thrown out.
We can formulate such a fact: the number of such pairs will be about 51/121 of the total number of pairs (think why this is so). Unfortunately, we will need to save two arrays of such pairs (for the sum and for the difference), which will give a gain on memory only 102/121. Well, 15% is also a reduction. But then we will have to run a little less along these arrays.
And, finally, the most good news: now it makes sense for us to sort out one of the variables (which is the most external in the cubic solution) in steps of 11. The bad news is that it will be necessary to solve both types of equations separately. The saddest thing about all this is: alas, it will speed up the program just 11 times (in fact, not yet a fact), instead of 11 5 times, as in decision # 6.
Here, with the reallocation of vectors, there is more luck and the program for n = 10,000 fits into 2GB.
Alas, the program has accelerated only 4.5 times. It seems that numerous checks in the second equation have seriously tainted the hidden constant. Do not worry, there is still room for optimization. The biggest problem now: wild memory consumption. If in time for the current record n is already tolerable, then we no longer fit in memory.
Pros: probably the fastest solution proposed.
Cons: still a problem with large memory consumption.
How do we reduce memory consumption? Let's use the trick described here . Namely: let's take some prime number p greater than n, but not much. Consider the first equation that we have (the second equation is treated similarly):
(a 5 + b 5 ) + (c 5 + d 5 ) = e 5 ; e = 0 mod 11
Now let (a 5 + b 5 ) = w mod p for some w from 0 to p-1. Then the number of pairs (a, b) that satisfy this comparison is a linear amount. To show this, let's look at the parameter a from 1 to n. Then, in order to find b, we will have to solve the comparison b 5 = (w - a 5 ) = u mod p. And it is argued that this comparison will always have no more than one solution. It follows this from this page on e-maxx . There you need to pay attention to the formula for obtaining all solutions from one:
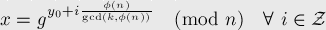
That is, the total solutions we have are gcd (5, phi (p)) = gcd (5, p-1). From this, we obtain that if p = 5q + 1, then we have 5 solutions (or none), and in the remaining cases - no more than one solutions.
(By the way, I have no idea where this formula comes from and how it works. If anyone knows the source, where it is clearly described, please share the link.)
Now the question is how to find the value b for a fixed u? To do this one time, but quickly - you need to understand the theory of numbers quite a lot. But we need b for all possible values of u, so we can simply find u for each b, and write it in a label: for such u, this is b.
Further, for fixed w and fixed e 5 , we get that (c 5 + d 5 ) = (e 5 - w) mod p. There is also a linear number of couples satisfying the comparison.
That is, for a fixed w and a fixed e, we get a linear number of pairs that need to be sorted (unfortunately, an extra logarithm of asymptotics comes out here), after which we walk with two pointers. Since different values of w and e are of order O (n), the total asymptotic behavior is O (n 3 log n).
Let's write a trial scary code:
Run this cruel tin:
Gentlemen, welcome back to the stone age! Why is it so slow is something godless? Oh yeah, there is now the power5 () function at the very bottom of three nested loops, within which the loop is already at 63 iterations. Rewrite on intrinsiki? Calmly, in the next solution, we will simply drag the answer from the pre-calculated label.
But now it almost does not eat memory, and one very useful property appeared: now the task can be divided into independent subtasks, that is, “parallelize”, or rather, distribute the calculations into several cores. Namely: for each kernel, to give its own values of the parameter w and when these w cover all the numbers from 0 to p-1, we cover all cases in the problem, and the load on all the kernels will be distributed approximately evenly.
Pros:consumes very little memory, supports distributed computing.
Cons: brakes like a shoemaker with a hangover.
We take solution # 9 and add hardcore optimizations. Well, in fact, they are not so hardcore. But there are many:
And we get the code:
The code has become smaller, simpler and kinder, or something. And he became faster:
We checked all the options for n = 10,000 for a more or less acceptable time, using some miserable 10 MB of memory.
Pros: fast enough, eats little memory.
Cons: they are not.
And NOW I pull out a 64-bit compiler, 6-core i7-5820K 3.3GHz and 4-core i7-3770 3.4GHz from wide-legged pants and run solution # 10 in 16 independent threads for several days.
A 64-bit program on a faster machine (remember, I previously tested the code on the i5-2410M 2.3Ghz) works about 2 times faster. As a result, we managed to drag n = 100000 and find the second solution to the desired Diophantine equation:
55 5 + 3183 5 + 28969 5 + 85282 5 = 85359 5
This is how the not the fastest solution with the not the fastest asymptotics is best in practice.
In theory, the code can still be accelerated or the logarithm can be cut off from the asymptotics, but at the moment I am tired of optimizing - I have already lost enough time . There are two solutions to the logarithm: replace quick sort with radix sort (but then the constant will increase to cosmic dimensions), or use a hash table instead of the idea of two pointers (you should write and see what is really faster here). Profiling showed that for n = 10,000 the sorting takes about half of the total time, that is, for our small values of n, the logarithm is quite tolerable. As for acceleration: there are probably some other tricks with modules that can speed up the program by 5-10 times.
I also have a wild idea to check all n up to a million. The expected verification time is, in principle, real - about a million cores. But my capacity for this will be clearly not enough. Drag along? However, I did not find information about how much n had already been sorted out. Maybe a million look no longer makes sense, because everything has long been counted. Please unsubscribe if anyone has information about this.

As you know, in order to solve any complex computational problem, you need to pay attention to at least the following points:
- Efficient algorithm
- Quick implementation
- Powerful iron
- Paralleling
I paid the most attention to the first item. Let's see what came of it.
Immediately, I note that the code was written in C ++, the 32-bit MS Visual C ++ 2008 Compiler was compiled and started in one stream on the i5-2410M 2.3Ghz machine. It's just more convenient for me - to write code lying on a not very powerful laptop, and to set the 64-bit compiler too lazy. Measurements of time do not shine with accuracy, since the code was rarely run more than 1 time per measurement, while other processes like the browser could slightly affect the running time. However, for our purposes, the accuracy is acceptable.
')
And yet, with the filing of Dimchansky , I’ll clarify that I will look for integer solutions of the above equation for a, b, c, d, e> 0, of which exactly 2 pieces are known. There is a third solution, but there variables can take negative values. You can find them all here .
Tale # 1 for O (n 5 )
Let's start with the dumbest decision that can be. Code:
Code
long long gcd( long long x, long long y ) { while (x&&y) x>y ? x%=y : y%=x; return x+y; } void tale1( int n ) { for (int a=1; a<=n; a++) for (int b=a+1; b<=n; b++) for (int c=b+1; c<=n; c++) for (int d=c+1; d<=n; d++) for (int e=d+1; e<=n; e++) { long long a5 = (long long)a*a*a*a*a; long long b5 = (long long)b*b*b*b*b; long long c5 = (long long)c*c*c*c*c; long long d5 = (long long)d*d*d*d*d; long long e5 = (long long)e*e*e*e*e; if (a5 + b5 + c5 + d5 == e5) if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e ); } } In fact, this is not the most stupid, because you can drive all the variables from 1 to n and at the end check that a <b <c <d <e. But then I would have had to wait too long. Working hours:
| n | Time |
|---|---|
| 100 | 1563ms |
| 200 | 40s |
| 500 | 74m |
Pros: simple as a boot, spelled quickly, requires O (1) memory, finds the classic solution 27 5 + 84 5 + 110 5 + 133 5 = 144 5 .
Cons: it is inhibited .
Tale # 2 for O (n 4 log n)
Let's speed up our decision a bit. In fact, this option is equivalent to what was proposed by comrade drBasic .
Code
void tale2( int n ) { vector< pair< long long, int > > vec; for (int a=1; a<=n; a++) vec.push_back( make_pair( (long long)a*a*a*a*a, a ) ); for (int a=1; a<=n; a++) for (int b=a+1; b<=n; b++) for (int c=b+1; c<=n; c++) for (int d=c+1; d<=n; d++) { long long a5 = (long long)a*a*a*a*a; long long b5 = (long long)b*b*b*b*b; long long c5 = (long long)c*c*c*c*c; long long d5 = (long long)d*d*d*d*d; long long sum = a5+b5+c5+d5; vector< pair< long long, int > >::iterator it = lower_bound( vec.begin(), vec.end(), make_pair( sum, 0 ) ); if (it != vec.end() && it->first==sum) if (gcd( a, gcd( gcd( b, c ), gcd( d, it->second ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, it->second ); } } Here we create an array, where we save the fifth powers of all numbers from 1 to n, then inside the four nested loops we use a binary search to check if there is a 5 + b 5 + c 5 + d 5 number in the array or not.
| n | Time # 1 | Time # 2 |
|---|---|---|
| 100 | 1563ms | 318ms |
| 200 | 40s | 4140ms |
| 500 | 74m | 189s |
| 1000 | 55m |
This option is already running faster, I even had the patience to wait for the end of the program for n = 1000.
Pros: still quite simple, faster than a stupid solution, it is easy to write, it finds a classic solution.
Cons: O (n) memory required, still slow .
Tale # 3 for O (n 4 log n), but with O (1) memory
In fact, it makes no sense to store all the degrees in an array and look for something binpoisk there. We already know what number in this array is at position i. You can simply run a bin-search on a “virtual” array. No sooner said than done:
Code
void tale3( int n ) { for (int a=1; a<=n; a++) for (int b=a+1; b<=n; b++) for (int c=b+1; c<=n; c++) for (int d=c+1; d<=n; d++) { long long a5 = (long long)a*a*a*a*a; long long b5 = (long long)b*b*b*b*b; long long c5 = (long long)c*c*c*c*c; long long d5 = (long long)d*d*d*d*d; long long sum = a5+b5+c5+d5; if (sum <= (long long)n*n*n*n*n) { int mi = d, ma = n; // invariant: for mi <, for ma >= while ( mi+1 < ma ) { int s = ((mi+ma)>>1); long long tmp = (long long)s*s*s*s*s; if (tmp < sum) mi = s; else ma = s; } if (sum == (long long)ma*ma*ma*ma*ma) if (gcd( a, gcd( gcd( b, c ), gcd( d, ma ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, ma ); } } } Now the array is not needed, we have pure binary search.
| n | Time # 1 | Time # 2 | Time # 3 |
|---|---|---|---|
| 100 | 1563ms | 318ms | 490ms |
| 200 | 40s | 4140ms | 6728ms |
| 500 | 74m | 189s | 352s |
| 1000 | 55m |
Unfortunately, the execution time has sunk, probably due to the fact that inside bin search we re-calculate the fifth power every time. Well, okay.
Pros: requires O (1) memory, finds a classic solution.
Cons: slower than the previous decision.
Fairy tale # 4 for O (n 4 )
Let's look at our equation again:
a 5 + b 5 + c 5 + d 5 = e 5
or, for simplicity, A = B.
Let the algorithm executes our 4 nested loops. Fix the values of a, b and c and see how the values of d and e behave. Let for some d = x the smallest value of e, for which A <= B, is equal to y. For d = x, it makes no sense to consider the values of e> y. Note also that for d = x + 1 the smallest value of e, for which A <= B, is not less than y. That is, we can always just gently increase the value of e while we go by d and this ensures that we do not miss anything. Since the values of d and e only increase, the total pass through them will take O (n). This idea is called the two-pointer method.
Code
void tale4( int n ) { for (int a=1; a<=n; a++) for (int b=a+1; b<=n; b++) for (int c=b+1; c<=n; c++) { int e = c+1; for (int d=c+1; d<=n; d++) { long long a5 = (long long)a*a*a*a*a; long long b5 = (long long)b*b*b*b*b; long long c5 = (long long)c*c*c*c*c; long long d5 = (long long)d*d*d*d*d; long long sum = a5+b5+c5+d5; while (e<n && (long long)e*e*e*e*e < sum) e++; if (sum == (long long)e*e*e*e*e) if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e ); } } } The code is less than for bin search, and there is more benefit.
| n | Time # 1 | Time # 2 | Time # 3 | Time # 4 |
|---|---|---|---|---|
| 100 | 1563ms | 318ms | 490ms | 360ms |
| 200 | 40s | 4140ms | 6728ms | 4339ms |
| 500 | 74m | 189s | 352s | 177s |
| 1000 | 55m | 46m |
Because of the large hidden constant, this solution starts to overtake solution # 2 by O (n 4 log n) only when n is about 500. It can, of course, be accelerated by calculating the fifth degrees more thoughtfully, but we will not do that.
Pros: asymptotically faster solution # 2, requires O (1) memory. Yes, it does.
Cons: far from the optimum, a large hidden constant.
Fairy tale # 5 for O (n 3 )
Let's develop an idea with two pointers, and turn the rest of the decision upside down. Suppose we have the equation A + B = C, and for each of the A, B, C we have n (A), n (B), n (C) ways to choose them. Let's fix some value C, and sort all valid values for A and B by ascending order. Then we can run on the values of A and B with the help of two pointers and for O (n (A) + n (B)) check everything you need for the current value of C! Namely: for some fixed A we will decrease the value of B, while A + B> C. As soon as A + B <= C becomes, then there is no point in reducing B. Then we increase A and continue the process of decreasing B. The whole algorithm will take completely O (n (A) log n (A) + n (B) log n (B) + (n (A) + n (B)) n ( WITH) ).
For the case when A and B are elements of the same set, the algorithm for checking fixed C can be stopped as soon as the current A and B meet (since, without loss of generality, we can assume that A <B).
Now in our equation we denote (a 5 + b 5 ) for A, (c 5 + d 5 ) for B, and e 5 for C. And write the following code:
Code
void tale5( int n ) { vector< pair< long long, int > > vec; for (int a=1; a<=n; a++) for (int b=a+1; b<=n; b++) { long long a5 = (long long)a*a*a*a*a; long long b5 = (long long)b*b*b*b*b; if (a5 + b5 < (long long)n*n*n*n*n) // avoid overflow for n<=5000 vec.push_back( make_pair( a5+b5, (a<<16)+b ) ); } sort( vec.begin(), vec.end() ); for (int e=1; e<=n; e++) { long long e5 = (long long)e*e*e*e*e; int i = 0, j = (int)vec.size()-1; while( i < j ) { while ( i < j && vec[i].first + vec[j].first > e5 ) j--; if ( vec[i].first + vec[j].first == e5 ) { int a = (vec[i].second >> 16); int b = (vec[i].second & ((1<<16)-1)); int c = (vec[j].second >> 16); int d = (vec[j].second & ((1<<16)-1)); if (b < c && gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e ); } i++; } } } Since the pairs (a, b) (and (c, d)) are of the order of n 2 , the sorting will take O (n 2 log n), and the next check using pointers is O (n 3 ). Total clean cube.
Exercise . Find the logical error in the code above.
Think a couple of minutes before watching the answer.
In our case, in the sorted array, theoretically, the same sums can get caught and then the two pointers can skip some equalities. But in fact they will be all different from the following reasoning: if there are coincidences, then x ^ 5 + y ^ 5 = z ^ 5 + t ^ 5 for some x, y, z, t and we found a counterexample to this hypothesis . As a fix, the simplest thing you can do is check that all numbers are really different.
| n | #one | # 2 | # 3 | #four | #five |
|---|---|---|---|---|---|
| 100 | 1563ms | 318ms | 490ms | 360ms | 82ms |
| 200 | 40s | 4140ms | 6728ms | 4339ms | 121ms |
| 500 | 74m | 189s | 352s | 177s | 516ms |
| 1000 | 55m | 46m | 3119ms | ||
| 2000 | 22s | ||||
| 5000 | 328s |
Significant acceleration allows you to drag n = 5000 for a reasonable time. Checks when adding pairs to an array are needed to avoid overflow.
Pros: probably the fastest asymptotic algorithm.
Cons: a large hidden constant, works only up to n of the order of 5000, eats even O (n 2 ) memory.
Tale # 6 for O (n 4 log n) with an incredibly small hidden constant
Suddenly. From the user's submission of erwins22 from this comment, we consider the residuals that we can get by dividing the fifth power by 11. That is, what a can be compared x 5 = a mod 11. It turns out that the possible values of a are 0, 1 and -1 (mod 11) (check for yourself and make sure).
Then, in the equality a 5 + b 5 + c 5 + d 5 = e 5 units and minus ones, the total even number (they must balance each other so that the parity converges), it follows that one of the numbers a, b, c, d, e is comparable from 0 to module 11, that is, divisible by 11. Let's put it separately in one direction, we get one of two options:
(a 5 + b 5 ) + (c 5 + d 5 ) = e 5 ; e = 0 mod 11
(e 5 - a 5 ) - (b 5 + c 5 ) = d 5 ; d = 0 mod 11
You will not believe, but if the number x is divisible by 11, then the number x 5 is divisible by 161051. Hence, the left-hand side of the above equalities must also be divisible by 161051. As you can see, in the equations above, some numbers are already carefully paired with brackets. Now, if we fix the first bracket, then the second bracket can have only one of all possible 161051 residues when divided by 161051. Thus, for each of O (n 2 ) first brackets, on average, there are O (n 2/161051) second. If we now sort out all of them and see if the result is an exact fifth degree (for example, a binoisk in an array of fifth degrees), then we will find all the solutions in O (n 4 log n / 161051). Code:
Code
void tale5( int n ) { vector< pair< long long, int > > vec; for (int a=1; a<=n; a++) for (int b=a+1; b<=n; b++) { long long a5 = (long long)a*a*a*a*a; long long b5 = (long long)b*b*b*b*b; if (a5 + b5 < (long long)n*n*n*n*n) // avoid overflow for n<=5000 vec.push_back( make_pair( a5+b5, (a<<16)+b ) ); } vector< pair< long long, int > > pows; for (int a=1; a<=n; a++) pows.push_back( make_pair( (long long)a*a*a*a*a, a ) ); // a^5 + b^5 + c^5 + d^5 = e^5 for (int a=1; a<=n; a++) for (int b=a+1; b<=n; b++) { long long a5 = (long long)a*a*a*a*a; long long b5 = (long long)b*b*b*b*b; long long rem = (z - (a5+b5)%z)%z; for (int i=0; i<(int)vec[rem].size(); i++) { long long sum = a5 + b5 + vec[rem][i].first; vector< pair< long long, int > >::iterator it = lower_bound( pows.begin(), pows.end(), make_pair( sum, 0 ) ); if (it != pows.end() && sum == it->first) { int c = (vec[rem][i].second >> 16); int d = (vec[rem][i].second & ((1<<16)-1)); int e = it->second; if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e ); } } } // e^5 - a^5 - b^5 - c^5 = d^5 for (int e=1; e<=n; e++) for (int a=1; a<e; a++) { long long e5 = (long long)e*e*e*e*e; long long a5 = (long long)a*a*a*a*a; long long rem = (e5-a5)%z; for (int i=0; i<(int)vec[rem].size(); i++) if (e5-a5 > vec[rem][i].first) { long long sum = e5 - a5 - vec[rem][i].first; vector< pair< long long, int > >::iterator it = lower_bound( pows.begin(), pows.end(), make_pair( sum, 0 ) ); if (it != pows.end() && sum == it->first) { int b = (vec[rem][i].second >> 16); int c = (vec[rem][i].second & ((1<<16)-1)); int d = it->second; if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e ); } } } } The working time of this solution:
| n | #one | # 2 | # 3 | #four | #five | # 6 |
|---|---|---|---|---|---|---|
| 100 | 1563ms | 318ms | 490ms | 360ms | 82ms | 129ms |
| 200 | 40s | 4140ms | 6728ms | 4339ms | 121ms | 140ms |
| 500 | 74m | 189s | 352s | 177s | 516ms | 375ms |
| 1000 | 55m | 46m | 3119ms | 2559ms | ||
| 2000 | 22s | 38s | ||||
| 5000 | 328s | 28m |
From the table it can be seen that for n = 500 and n = 1000 this solution even overtakes the cubic one. But then the cubic solution still begins to overtake. Asymptotics she is - you can not fool her.
Pros: very powerful clipping.
Cons: a large asymptotic, it is not clear how to fasten this idea to a cubic solution.
Tale # 7 for O (n 3 ) with 128-bit numbers
Let us temporarily forget about the tricks with the modules (we will remember from later on a bit later!) And redo our cubic solution so that it can work correctly for n> 5000. To do this, we implement 128-bit integers.
Code
typedef unsigned long long uint64; typedef pair< uint64, uint64 > uint128; uint128 operator+ (const uint128 & a, const uint128 & b) { uint128 re = make_pair( a.first + b.first, a.second + b.second ); if ( re.second < a.second ) re.first++; return re; } uint128 operator- (const uint128 & a, const uint128 & b) { uint128 re = make_pair( a.first - b.first, a.second - b.second ); if ( re.second > a.second ) re.first--; return re; } uint128 power5( int x ) { uint64 x2 = (uint64)x*x; uint64 x3 = (uint64)x2*x; uint128 re = make_pair( (uint64)0, (uint64)0 ); uint128 cur = make_pair( (uint64)0, x3 ); for (int i=0; i<63; i++) { if ((x2>>i)&1) re = re + cur; cur = cur + cur; } return re; } void tale7( int n ) { vector< pair< uint128, int > > vec = vector< pair< uint128, int > >( n*n/2 ); uint128 n5 = power5( n ); int ind = 0; for (int a=1; a<=n; a++) for (int b=a+1; b<=n; b++) { uint128 a5 = power5( a ); uint128 b5 = power5( b ); if (a5 + b5 < n5) vec[ind++] = make_pair( a5+b5, (a<<16)+b ); } sort( vec.begin(), vec.begin()+ind ); for (int e=1; e<=n; e++) { uint128 e5 = power5( e ); int i = 0, j = ind-1; while( i < j ) { while ( i < j && vec[i].first + vec[j].first > e5 ) j--; if ( vec[i].first + vec[j].first == e5 ) { int a = (vec[i].second >> 16); int b = (vec[i].second & ((1<<16)-1)); int c = (vec[j].second >> 16); int d = (vec[j].second & ((1<<16)-1)); if (b < c && gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e ); } i++; } } } The operations that needed to be added are addition and construction to the fifth degree. There is still a subtraction, in this solution it is not needed, but it will be needed later. So let it be. Since the 128-bit number is implemented as pair, there are already operations <,>, =, and they work exactly as we need.
At the very beginning we immediately set the size of the vector. It’s not that this is done for optimization, I’m still too lazy to uncover the 64-bit compiler, and only 2GB of memory is available on 32 bits. Now for n = 10,000 it takes about 1.2GB per vector. If you expand the vector via push_back, then at the very end it captures more than 2 GB during reallocation (to increase from the length N to 2 * N you need 3 * N intermediate memory).
| n | #one | # 2 | # 3 | #four | #five | # 6 | # 7 |
|---|---|---|---|---|---|---|---|
| 100 | 1563ms | 318ms | 490ms | 360ms | 82ms | 129ms | 20ms |
| 200 | 40s | 4140ms | 6728ms | 4339ms | 121ms | 140ms | 105ms |
| 500 | 74m | 189s | 352s | 177s | 516ms | 375ms | 1014ms |
| 1000 | 55m | 46m | 3119ms | 2559ms | 7096ms | ||
| 2000 | 22s | 38s | 52s | ||||
| 5000 | 328s | 28m | 13m | ||||
| 10,000 | 89m |
You can see that now the program has slowed down almost exactly 2 times with respect to solution # 5, but we have conquered the new impregnable vertex n = 10,000!
Pros: now does not overflow for n> 5000.
Cons: running 2 times slower than the solution # 5, eats a lot of memory.
Tale # 8 for O (n 3 ) with a smaller hidden constant
Recall again the remnants of division by 11. We have two equalities:
(a 5 + b 5 ) + (c 5 + d 5 ) = e 5 ; e = 0 mod 11
(e 5 - a 5 ) - (b 5 + c 5 ) = d 5 ; d = 0 mod 11
Recall that the fifth degree modulo 11 always have residues 0, 1, or -1. We remove the restrictions of the form a <b <c <d and allow numbers to arbitrarily move from one bracket to another. Then it is easy to show (by considering all cases) that they can always be moved so that each of the brackets will be equal to 0 modulo 11. Well, now we will need to go through all the pairs of numbers from 1 to n, find the sum and difference of their fifth degrees and remember only those that are divided by 11. And the remaining pairs can simply be thrown out.
We can formulate such a fact: the number of such pairs will be about 51/121 of the total number of pairs (think why this is so). Unfortunately, we will need to save two arrays of such pairs (for the sum and for the difference), which will give a gain on memory only 102/121. Well, 15% is also a reduction. But then we will have to run a little less along these arrays.
And, finally, the most good news: now it makes sense for us to sort out one of the variables (which is the most external in the cubic solution) in steps of 11. The bad news is that it will be necessary to solve both types of equations separately. The saddest thing about all this is: alas, it will speed up the program just 11 times (in fact, not yet a fact), instead of 11 5 times, as in decision # 6.
Code
void tale8( int n ) { vector< pair< uint128, pair< int, int > > > vec_p, vec_m; uint128 n5 = power5( n ); for (int a=1; a<=n; a++) for (int b=1; b<a; b++) { uint128 a5 = power5( a ); uint128 b5 = power5( b ); int A = a%11; int B = b%11; int A5 = (A*A*A*A*A)%11; int B5 = (B*B*B*B*B)%11; if ( (A5+B5)%11 == 0 ) vec_p.push_back( make_pair( a5+b5, make_pair( a, b ) ) ); if ( (A5-B5+11)%11 == 0) vec_m.push_back( make_pair( a5-b5, make_pair( a, b ) ) ); } sort( vec_p.begin(), vec_p.end() ); sort( vec_m.begin(), vec_m.end() ); // (a^5 + b^5) + (c^5 + d^5) = e^5 for (int e=11; e<=n; e+=11) { uint128 e5 = power5( e ); int i = 0, j = (int)vec_p.size()-1; while( i < j ) { while ( i < j && vec_p[i].first + vec_p[j].first > e5 ) j--; if ( vec_p[i].first + vec_p[j].first == e5 ) { int a = vec_p[i].second.first; int b = vec_p[i].second.second; int c = vec_p[j].second.first; int d = vec_p[j].second.second; if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e ); } i++; } } // (e^5 - a^5) - (b^5 + c^5) = d^5 for (int d=11; d<=n; d+=11) { uint128 d5 = power5( d ); int i = 0, j = 0, mx_i = (int)vec_m.size(), mx_j = (int)vec_p.size(); while (i < mx_i && j < mx_j) { while (j < mx_j && vec_m[i].first > vec_p[j].first && vec_m[i].first - vec_p[j].first > d5) j++; if ( j < mx_j && vec_m[i].first > vec_p[j].first && vec_m[i].first - vec_p[j].first == d5 ) { int e = vec_m[i].second.first; int a = vec_m[i].second.second; int b = vec_p[j].second.first; int c = vec_p[j].second.second; if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e ); } i++; } } } Here, with the reallocation of vectors, there is more luck and the program for n = 10,000 fits into 2GB.
| n | #one | # 2 | # 3 | #four | #five | # 6 | # 7 | #eight |
|---|---|---|---|---|---|---|---|---|
| 100 | 1563ms | 318ms | 490ms | 360ms | 82ms | 129ms | 20ms | 16ms |
| 200 | 40s | 4140ms | 6728ms | 4339ms | 121ms | 140ms | 105ms | 49ms |
| 500 | 74m | 189s | 352s | 177s | 516ms | 375ms | 1014ms | 472ms |
| 1000 | 55m | 46m | 3119ms | 2559ms | 7096ms | 2110ms | ||
| 2000 | 22s | 38s | 52s | 13s | ||||
| 5000 | 328s | 28m | 13m | 161s | ||||
| 10,000 | 89m | 20m |
Alas, the program has accelerated only 4.5 times. It seems that numerous checks in the second equation have seriously tainted the hidden constant. Do not worry, there is still room for optimization. The biggest problem now: wild memory consumption. If in time for the current record n is already tolerable, then we no longer fit in memory.
Pros: probably the fastest solution proposed.
Cons: still a problem with large memory consumption.
Tale # 9 for O (n 3 log n) with memory consumption O (n)
How do we reduce memory consumption? Let's use the trick described here . Namely: let's take some prime number p greater than n, but not much. Consider the first equation that we have (the second equation is treated similarly):
(a 5 + b 5 ) + (c 5 + d 5 ) = e 5 ; e = 0 mod 11
Now let (a 5 + b 5 ) = w mod p for some w from 0 to p-1. Then the number of pairs (a, b) that satisfy this comparison is a linear amount. To show this, let's look at the parameter a from 1 to n. Then, in order to find b, we will have to solve the comparison b 5 = (w - a 5 ) = u mod p. And it is argued that this comparison will always have no more than one solution. It follows this from this page on e-maxx . There you need to pay attention to the formula for obtaining all solutions from one:
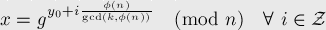
That is, the total solutions we have are gcd (5, phi (p)) = gcd (5, p-1). From this, we obtain that if p = 5q + 1, then we have 5 solutions (or none), and in the remaining cases - no more than one solutions.
(By the way, I have no idea where this formula comes from and how it works. If anyone knows the source, where it is clearly described, please share the link.)
Now the question is how to find the value b for a fixed u? To do this one time, but quickly - you need to understand the theory of numbers quite a lot. But we need b for all possible values of u, so we can simply find u for each b, and write it in a label: for such u, this is b.
Further, for fixed w and fixed e 5 , we get that (c 5 + d 5 ) = (e 5 - w) mod p. There is also a linear number of couples satisfying the comparison.
That is, for a fixed w and a fixed e, we get a linear number of pairs that need to be sorted (unfortunately, an extra logarithm of asymptotics comes out here), after which we walk with two pointers. Since different values of w and e are of order O (n), the total asymptotic behavior is O (n 3 log n).
Let's write a trial scary code:
Code
bool is_prime( int x ) { if (x<2) return false; for (int a=2; a*a<=x; a++) if (x%a==0) return false; return true; } void tale9( int n ) { int p = n+1; while ( p%5==1 || !is_prime( p ) ) p++; vector< int > sols = vector< int >( p, -1 ); for (int i=1; i<=n; i++) { uint64 tmp = ((uint64)i*i)%p; tmp = (((tmp*tmp)%p)*i)%p; sols[(unsigned int)tmp] = i; } for (int w=0; w<p; w++) { // (a^5 + b^5) + (c^5 + d^5) = e^5 // (a^5 + b^5) = w (mod p) vector< pair< uint128, pair< int, int > > > vec1; for (int a=1; a<=n; a++) { uint64 a5p = ((uint64)a*a)%p; a5p = ((a5p*a5p)%p*a)%p; int b = sols[ (w - a5p + p)%p ]; if (b!=-1 && b<a) { uint128 a5 = power5( a ); uint128 b5 = power5( b ); int A = a%11, A5 = (A*A*A*A*A)%11; int B = b%11, B5 = (B*B*B*B*B)%11; if ( (A5+B5)%11 == 0 ) vec1.push_back( make_pair( a5+b5, make_pair( a, b ) ) ); } } sort( vec1.begin(), vec1.end() ); for (int e=11; e<=n; e+=11) { // (a^5 + b^5) + (c^5 + d^5) = e^5 // (a^5 + b^5) = w (mod p) // (c^5 + d^5) = (e^5 - w) = q (mod p) uint64 e5p = ((uint64)e*e)%p; e5p = ((e5p*e5p)%p*e)%p; int q = (int)((e5p - w + p)%p); vector< pair< uint128, pair< int, int > > > vec2; for (int c=1; c<=n; c++) { uint64 c5p = ((uint64)c*c)%p; c5p = ((c5p*c5p)%p*c)%p; int d = sols[ (q - c5p + p)%p ]; if (d!=-1 && d<c) { uint128 c5 = power5( c ); uint128 d5 = power5( d ); int C = c%11, C5 = (C*C*C*C*C)%11; int D = d%11, D5 = (D*D*D*D*D)%11; if ( (C5+D5)%11 == 0 ) vec2.push_back( make_pair( c5+d5, make_pair( c, d ) ) ); } } sort( vec2.begin(), vec2.end() ); uint128 e5 = power5( e ); int i = 0, j = (int)vec2.size()-1, mx_i = (int)vec1.size(); while( i < mx_i && j >= 0 ) { while ( j >= 0 && vec1[i].first + vec2[j].first > e5 ) j--; if ( j >= 0 && vec1[i].first + vec2[j].first == e5 ) { int a = vec1[i].second.first; int b = vec1[i].second.second; int c = vec2[j].second.first; int d = vec2[j].second.second; if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e ); } i++; } } // (e^5 - a^5) - (b^5 + c^5) = d^5 // (b^5 + c^5) = w (mod p) // already computed as vec1 for (int d=11; d<=n; d+=11) { // (e^5 - a^5) = (d^5 + w) = q (mod p) uint64 d5p = ((uint64)d*d)%p; d5p = ((d5p*d5p)%p*d)%p; int q = (int)((d5p + w)%p); vector< pair< uint128, pair< int, int > > > vec2; for (int e=1; e<=n; e++) { uint64 e5p = ((uint64)e*e)%p; e5p = ((e5p*e5p)%p*e)%p; int a = sols[ (e5p - q + p)%p ]; if (a!=-1 && a<e) { uint128 e5 = power5( e ); uint128 a5 = power5( a ); int E = e%11, E5 = (E*E*E*E*E)%11; int A = a%11, A5 = (A*A*A*A*A)%11; if ( (E5-A5+11)%11 == 0 ) vec2.push_back( make_pair( e5-a5, make_pair( e, a ) ) ); } } sort( vec2.begin(), vec2.end() ); uint128 d5 = power5( d ); int i = 0, j = 0, mx_i = (int)vec2.size(), mx_j = (int)vec1.size(); while (i < mx_i && j < mx_j) { while (j < mx_j && vec2[i].first > vec1[j].first && vec2[i].first - vec1[j].first > d5) j++; if ( j < mx_j && vec2[i].first > vec1[j].first && vec2[i].first - vec1[j].first == d5 ) { int e = vec2[i].second.first; int a = vec2[i].second.second; int b = vec1[j].second.first; int c = vec1[j].second.second; if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e ); } i++; } } } } Run this cruel tin:
| n | #one | # 2 | # 3 | #four | #five | # 6 | # 7 | #eight | #9 |
|---|---|---|---|---|---|---|---|---|---|
| 100 | 1563ms | 318ms | 490ms | 360ms | 82ms | 129ms | 20ms | 16ms | 219ms |
| 200 | 40s | 4140ms | 6728ms | 4339ms | 121ms | 140ms | 105ms | 49ms | 1741ms |
| 500 | 74m | 189s | 352s | 177s | 516ms | 375ms | 1014ms | 472ms | 25s |
| 1000 | 55m | 46m | 3119ms | 2559ms | 7096ms | 2110ms | 200s | ||
| 2000 | 22s | 38s | 52s | 13s | 28m | ||||
| 5000 | 328s | 28m | 13m | 161s | |||||
| 10,000 | 89m | 20m |
Gentlemen, welcome back to the stone age! Why is it so slow is something godless? Oh yeah, there is now the power5 () function at the very bottom of three nested loops, within which the loop is already at 63 iterations. Rewrite on intrinsiki? Calmly, in the next solution, we will simply drag the answer from the pre-calculated label.
But now it almost does not eat memory, and one very useful property appeared: now the task can be divided into independent subtasks, that is, “parallelize”, or rather, distribute the calculations into several cores. Namely: for each kernel, to give its own values of the parameter w and when these w cover all the numbers from 0 to p-1, we cover all cases in the problem, and the load on all the kernels will be distributed approximately evenly.
Pros:consumes very little memory, supports distributed computing.
Cons: brakes like a shoemaker with a hangover.
Tale # 10 for O (n 3 log n) with hardcore optimizations
We take solution # 9 and add hardcore optimizations. Well, in fact, they are not so hardcore. But there are many:
- We foresee everything that can only be pre-calculated and put them in plates.
- We reject vectors with their push_backs and redo everything into static arrays.
- Wherever possible, we remove the operations of taking the remainder of the division.
- In the arrays for couples, we now store only the sum (or difference) of the fifth degrees, and the couples themselves try to recover only if a solution is found (since solutions are very rare - the pair is looked for exactly by the square).
- The arrays that are generated inside the cycles of e and d are now 2 times shorter on average. Indeed, for the case of (a 5 + b 5 ) + (c 5 + d 5 ) = e 5, we are interested only in (c 5 + d 5 ) <e 5 (good for small e), and for (e 5 - a 5 ) - (b 5 + c 5 ) = d 5 we are interested only in (e 5 - a 5 )> d 5 (good for large d).
And we get the code:
Code
#define MAXN 100500 int pow5modp[MAXN]; int sols[MAXN]; uint128 vec1[MAXN], vec2[MAXN]; int vec1_sz, vec2_sz; uint128 pow5[MAXN]; int pow5mod11[MAXN]; void init_arrays( int n, int p ) { for (int i=1; i<=n; i++) { uint64 i5p = ((uint64)i*i)%p; i5p = (((i5p*i5p)%p)*i)%p; pow5modp[i] = (int)i5p; } for (int i=0; i<p; i++) sols[i] = -1; for (int i=1; i<=n; i++) sols[pow5modp[i]] = i; for (int i=1; i<=n; i++) pow5[i] = power5(i); for (int i=1; i<=n; i++) { int ii = i%11; pow5mod11[i] = (ii*ii*ii*ii*ii)%11; } } void tale10( int n, int start=0, int step=1 ) { int p = n+1; while ( p%5==1 || !is_prime( p ) ) p++; init_arrays( n, p ); for (int w=start; w<p; w+=step) { cerr << "n=" << n << " p=" << p << " w=" << w << "\n"; // (a^5 + b^5) + (c^5 + d^5) = e^5 // (a^5 + b^5) = w (mod p) vec1_sz = 0; for (int a=1; a<=n; a++) { int tmp = w - pow5modp[a]; int b = sols[ tmp<0 ? tmp+p : tmp ]; if (b!=-1 && b<a) if ( (pow5mod11[a]+pow5mod11[b])%11 == 0 ) vec1[vec1_sz++] = pow5[a]+pow5[b]; } sort( vec1, vec1 + vec1_sz ); for (int e=11; e<=n; e+=11) { // (a^5 + b^5) + (c^5 + d^5) = e^5 // (a^5 + b^5) = w (mod p) // (c^5 + d^5) = (e^5 - w) = q (mod p) int q = (int)((pow5modp[e] - w + p)%p); uint128 e5 = pow5[e]; vec2_sz = 0; for (int c=1; c<e; c++) { int tmp = q - pow5modp[c]; int d = sols[ tmp<0 ? tmp+p : tmp ]; if (d!=-1 && d<c) if ( pow5mod11[c]+pow5mod11[d]==0 || pow5mod11[c]+pow5mod11[d]==11 ) { uint128 s = pow5[c]+pow5[d]; if (s < e5) vec2[vec2_sz++] = s; } } sort( vec2, vec2 + vec2_sz ); int i = 0, j = vec2_sz-1, mx_i = vec1_sz-1; while( i < mx_i && j >= 0 ) { while ( j >= 0 && vec1[i] + vec2[j] > e5 ) j--; if ( j >= 0 && vec1[i] + vec2[j] == e5 ) { int a=-1, b=-1, c=-1, d=-1; for (int A=1; A<=n; A++) for (int B=1; B<A; B++) if (pow5[A]+pow5[B]==vec1[i]) { a=A; b=B; } for (int C=1; C<=n; C++) for (int D=1; D<C; D++) if (pow5[C]+pow5[D]==vec2[j]) { c=C; d=D; } if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e ); } i++; } } // (e^5 - a^5) - (b^5 + c^5) = d^5 // (b^5 + c^5) = w (mod p) // already computed as vec1 for (int d=11; d<=n; d+=11) { // (e^5 - a^5) = (d^5 + w) = q (mod p) int q = (int)((pow5modp[d] + w)%p); uint128 d5 = pow5[d]; vec2_sz = 0; for (int e=d+1; e<=n; e++) { int tmp = pow5modp[e]-q; int a = sols[ tmp<0 ? tmp+p : tmp ]; if (a!=-1 && a<e) if ( pow5mod11[e]==pow5mod11[a] ) { uint128 s = pow5[e]-pow5[a]; if (s > d5) vec2[vec2_sz++] = s; } } sort( vec2, vec2 + vec2_sz ); int i = 0, j = 0, mx_i = vec2_sz, mx_j = vec1_sz; while (i < mx_i && j < mx_j) { while (j < mx_j && vec2[i] > vec1[j] && vec2[i] - vec1[j] > d5) j++; if ( j < mx_j && vec2[i] > vec1[j] && vec2[i] - vec1[j] == d5 ) { int e=-1, a=-1, b=-1, c=-1; for (int E=1; E<=n; E++) for (int A=1; A<E; A++) if (pow5[E]-pow5[A]==vec2[i]) { e = E; a = A; } for (int B=1; B<=n; B++) for (int C=1; C<B; C++) if (pow5[B]+pow5[C]==vec1[j]) { b = B; c = B; } if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e ); } i++; } } } } The code has become smaller, simpler and kinder, or something. And he became faster:
| n | #one | # 2 | # 3 | #four | #five | # 6 | # 7 | #eight | #9 | #ten |
|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 1563ms | 318ms | 490ms | 360ms | 82ms | 129ms | 20ms | 16ms | 219ms | 8ms |
| 200 | 40s | 4140ms | 6728ms | 4339ms | 121ms | 140ms | 105ms | 49ms | 1741ms | 30ms |
| 500 | 74m | 189s | 352s | 177s | 516ms | 375ms | 1014ms | 472ms | 25s | 379ms |
| 1000 | 55m | 46m | 3119ms | 2559ms | 7096ms | 2110ms | 200s | 2993ms | ||
| 2000 | 22s | 38s | 52s | 13s | 28m | 24s | ||||
| 5000 | 328s | 28m | 13m | 161s | 405s | |||||
| 10,000 | 89m | 20m | 59m |
We checked all the options for n = 10,000 for a more or less acceptable time, using some miserable 10 MB of memory.
Pros: fast enough, eats little memory.
Cons: they are not.
Neither in a fairy tale, nor a pen to describe
And NOW I pull out a 64-bit compiler, 6-core i7-5820K 3.3GHz and 4-core i7-3770 3.4GHz from wide-legged pants and run solution # 10 in 16 independent threads for several days.
| n | Total cores | Real time | Streams |
|---|---|---|---|
| 10,000 | 29m | 29m | one |
| 20,000 | 318m | 58m | 6 |
| 50,000 | 105h | 7h | sixteen |
| 100,000 | 970h | 62h | sixteen |
Exact times for n = 100,000
00 221897112ms
01 221697012ms
02 221413313ms
03 219200228ms
04 222362721ms
05 221386814ms
06 221880726ms
07 219676217ms **
08 222212701ms
09 221865811ms
10 213299815ms *
11 211880251ms
12 211634584ms **
13 210114095ms
14 211691320ms *
15 212125515ms
* found 27^5 + 133^5 + 133^5 + 110^5 = 144^5
** found 85282^5 + 28969^5 + 28969^5 + 55^5 = 85359^5
00-09 : i7-5820K 3.3GHz
10-15 : i7-3770 3.4GHz
sum ~ 970h
max ~ 62hA 64-bit program on a faster machine (remember, I previously tested the code on the i5-2410M 2.3Ghz) works about 2 times faster. As a result, we managed to drag n = 100000 and find the second solution to the desired Diophantine equation:
55 5 + 3183 5 + 28969 5 + 85282 5 = 85359 5
Tale - a lie, but in her hint
This is how the not the fastest solution with the not the fastest asymptotics is best in practice.
In theory, the code can still be accelerated or the logarithm can be cut off from the asymptotics, but at the moment I am tired of optimizing - I have already lost enough time . There are two solutions to the logarithm: replace quick sort with radix sort (but then the constant will increase to cosmic dimensions), or use a hash table instead of the idea of two pointers (you should write and see what is really faster here). Profiling showed that for n = 10,000 the sorting takes about half of the total time, that is, for our small values of n, the logarithm is quite tolerable. As for acceleration: there are probably some other tricks with modules that can speed up the program by 5-10 times.
Drag?
I also have a wild idea to check all n up to a million. The expected verification time is, in principle, real - about a million cores. But my capacity for this will be clearly not enough. Drag along? However, I did not find information about how much n had already been sorted out. Maybe a million look no longer makes sense, because everything has long been counted. Please unsubscribe if anyone has information about this.
Here and the fairy-tale end, who mastered - well done!
Source: https://habr.com/ru/post/318244/
All Articles