Attempts to open a new checkers tactic or what to do with a pipe dream

Introduction

Sports game "Checkers" is one of the games of mankind, which the computer has not yet fully calculated. There is news that scientists have found a strategy in which the computer will never lose. During my 9 years dedicated to this game, I met only one program that I could not win. Perhaps my sports experience will make the assumption that it was a program that implements the strategy described above. To my great surprise, it occupied only 60 MB. Or maybe there was a well-trained neural network based on it? But I still can not believe that it is impossible to calculate them. There are only 10 ^ 20 positions, will my computer really not cope with such a task? And also, is there really no tactic in which at the beginning of the game the opponent gives up the piece and find themselves in a tactical advantage ?! Not a single debut of this I have not seen. I'm going to check ...

The implementation of the algorithm for solving combinational problems

The first attempt was made at the end of the 2nd course. After a qualitative study of the C language, I thought that it would not hurt to learn C ++. After watching a large number of lectures on this language, I wanted to take up some project. And he took up the checkers. More subtle work with variables allowed more efficient to spend time on the miscalculation of positions. If these actions are similar to actions with graphs, then this algorithm could be called a search in width. Stopping the work of the algorithm was the complete passage through the graph.

One object described the situation on the board. In one object was stored:

class Queue { public: Queue *pnr; /*pointer to next record*/ Queue *ppr; /*pointer to prev record*/ Map *pdb; /*pointer to draught board*/ char *action; /*actions of parents*/ Queue *pp; /*pointer to parent*/ Queue *pfc; /*pointer to first child*/ int nmd; /*Approval of the number of moves to a draw*/ int color; }; 

Since the search algorithm was implemented in width, the data could be stored in a doubly linked sheet, where pnr and ppr are pointers implementing this collection.
')

pdb - A pointer to the board layout.
action - information about the progress made by the parent, in order to achieve this position. It looked like a normal recording of moves in “c3 – d4” checkers when moving checkers or “c3: e5” at a wooden house. The variable was necessary for more accurate debugging of the situation.
pp , pfc - pointers to the parent and to the first generated position. Since the search algorithm was implemented in width, then all generated positions in the doubly linked list were located side by side, one after the other. Therefore, in order to save the data in the form of a tree, it is enough to store a pointer to the first child, and all other subsequent children referred to the same parent. This algorithm allowed the parent to retrieve the results of the children, that is, to analyze the current situation, looking only at what a given move may have engendered a child.
nmd - A number indicating how many moves are left before the game will be considered a draw. For example, in a situation of 3 queens versus the 1st, only 15 moves are allocated for the completion of the game. When you change the number of checkers, as well as after the formation of a checker dam, this number is recalculated.
color - Whose turn now.

I was very afraid of stack overflow and thought that it would still be better to pass pointers to functions, so I decided to avoid direct passing an object as a parameter. The implementation was simple: we take an element from the queue, consider it, giving rise to subsequent positions, then take the next element from the queue and so on in a circle.

Result:

Viewed: 61.133 items
Stored records in the queue: 264.050 positions
RAM (2 GB) ended only on such data. Such results are suitable only for short combinational problems.
But this way of working with checkers positions allowed me to thoroughly debug the work of the “core” of the program.

Transition to "version control system"

In the algorithm, a lot of memory was spent on saving data about the board. Each position required to allocate a section of memory. Moreover, how to encode the current checker layout better, I did not think:

 /* info about one checker */ class Checkers { public: chlive live; chstatus status; }; /* info about position a checker */ class PosCheckers { public: chcolor color; Checkers *ptrCheckers; }; /* battlefield */ class Map { public: PosCheckers coordinate[8][8]; }; 

color - Color checkers. Black, white, or empty.
ptrCheckers - If there are no checkers in this field, then we do not allocate memory.
status - Lady or saber.
live - whether checker is alive Only in order not to cut down this checker again.

I understand that instead of coordinate [8] [8], only coordinate [8] [4] could have been dispensed with, but understanding my own code would be very badly damaged.

In general, a lot of memory was required to maintain the position, so I decided to place the responsibility for identifying the checkers positions on the action - a record of the progress of the parent, which contained data like "c3-d4".

Now, when we take an element from the queue, we, starting from the very beginning. We take the initial position of the checkers and from it already on the way back, we execute the moves that attracted this child. Thus was the placement of the checkers on the board for each element of the queue.

Result:

Viewed: 1.845.265 items
Stored records in the queue: 8.209.054 positions

Rejection of the “version control system”; go to depth search

Unfortunately, the search in width had at least some significant problems: Sometimes he created the same constellations. And to recognize, already created party, at a large amount of data, it was laborious. It was also not clear what to do when we did not have enough memory. All the stored data was necessary to restore the ideological chain, so that if necessary, "scoop" from somewhere in the memory, it did not turn out.

The search “in depth” made it possible to move from problems of a local character (solutions of combinational problems) to global ones (miscalculation of the whole batch). This algorithm considers the current arrangement of checkers, giving rise to descendants, selects the first of them and assigns it to the current role. If there are no descendants, then we indicate that we have lost in this position and are moving on to considering the next placement with the parent.

Also in order not to calculate repeated positions in the presence of ladies, it was decided to look through all the positions of the parents. If there is one, I do not consider it, but turn to the next one.

It was decided to remove the great-grandchildren from the memory of the constellation, in which the result was known. Thereby it was possible to avoid its overflow. If overflow does not occur when searching for the deepest element.

It was also decided to add a new way of storing a position - a list of figures:

 class ListCheckers { public: ListCheckers *pnr; chcolor color; chstatus status; int x,y; /* coordinate */ }; 

With the help of it, we began to more quickly find the possibility of a felling, as well as sort out checkers to check the possibility of a move. Now our “position” object stored in the queue had the following fields:

 class Queue { public: ListCheckers *plch; /*pointer to list of checkers*/ ListChilds *pcs; /*pointer to list of childs*/ chcolor color; int draw; chresult result; }; 

I did not expect that the free command does not guarantee 100% memory freeing . When debugging, it turned out that after executing the free command, the memory was not released at all. Somewhere in the darkness of the forums, I learned that free only gives the OS instructions for freeing memory, and the OS itself decides whether to free memory or not. In general, the OS I was “greedy,” so I had to work with memory differently. I allocated memory as needed to hold the chain of the first "children." And instead of deleting the “first” child we reviewed, the data about him was overwritten with the data about the next child.

To this end, an element was developed responsible for dynamic work with memory:

 class MainQueue { public: MainQueue* parent; /*pointer to parent's record*/ MainQueue* next_record; /*pointer to child's record*/ Queue* now; /*pointer to record on data with position*/ int draw; };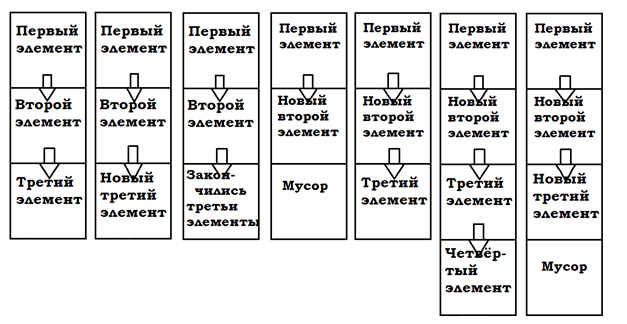 

Result:

For 1 day of continuous work:
created was 2.040.963 batches
seen was 1.241.938 lots
Occupied space on RAM: 1.378 MB

Work with files

Unfortunately, with such a choice of the next element we would have “hung up” for a long time with identical positions. Especially when miscalculations for the ladies. Therefore, I wanted to implement a database where the results of already viewed positions would be stored. Therefore, I decided to store data about each batch.

Avoiding memory problems, I ran into her again. Since I did not have enough RAM, I decided to use external media. I recorded all positions in the index.txt and queue.txt file. In queue.txt I kept data about each batch. And in index.txt - the batch ID and the location of information about this batch in queue.txt, that is, the offset. I wanted to compress the data, but leave it in a readable form. Because I thought that the finish was still far away. Therefore, I saved the data in the following form:

 queue.txt : aaaaeaaaaacaaaaa aaaaeaaaaaakaaaa 50 U Aaaaaaeaaacaaaaa Aaaaaaauaacaaaaa 49 U aaaaaaeakaaaaaaa aaaaaaeacaaaaaaa 48 W Aaaaaaaaaauaaaaa 47 L … index.txt : Aaaaeaaaaaaacaaa000000000000000000000 aaaaeaaaaacaaaaa000000000000000000040 aaaaeaaaaaakaaaa--------------------- Aaaaaaeaaacaaaaa000000000000000000080 Aaaaaaauaacaaaaa000000000000000000178 … 

On the board, a game cell can take 5 states: white / black checker, white / black woman, or empty. This means that the two cells will have 25 states in various combinations. Note that in the Latin alphabet there are 26 letters and it is quite suitable in order to describe the state of 2 playing cells at once in one letter. This means that the entire board with 32 game cells can be described by 16 letters of the Latin alphabet, which have a more or less readable form. It is also necessary to keep whose turn in this position. Then, if the first letter is capitalized, then the move is now black. We also need to remember the number of moves from the current placement, before making a positional draw. And also the result: W-win, L-lose, D-draw, U-unknown. And debugging did not become more difficult.

Result:

For two hours, the program required only 4 MB of RAM, but the parties calculated very little. In queue.txt there were 2918 records and was equal to 401 KB. The index.txt file contained 6095 entries and weighed 232 KB. At this rate, it will turn out to calculate only 500 million = 5 * 10 ^ 8 positions and my 1TB disk reported that it does not have enough memory. Yes, and it will happen very, very not soon. My calculated positions will have little effect on the game as a whole.

Data compression

I was able to come up with only 3 options for promoting the project:

1. 5 ^ 32 - various arrangements of figures,
   2 * 5 ^ 32 - considering whose move
   2 * (2 * 5 ^ 32) - the maximum amount of occupied space is ~ 9.32 * 10 ^ 22 bits , provided that it is sufficient for each arrangement to indicate the result equal to 2 bits.
   Moreover, in the normal party there are 5 * 10 ^ 20 different positions.
   So, about 2 * (2 * 5 * 10 ^ 20) = 2 * 10 ^ 21 bits will be informational, and the rest ~ (9.12 * 10 ^ 21) will mean that such an arrangement of checkers does not exist in this game.
   
   There is 1TB = 8 * 10 ^ 12 bits available
   It is necessary to develop a compression algorithm for this task, while maintaining fast data indexing.
   
   
2. In a normal game there are 5 * 10 ^ 20 different positions.
   For quick indexing, we will keep its “children” at each position, as well as the result. On average, a position has about Y descendants.
   
   Encode the "links" to descendants in X bits, and the result in 2 bits, as well as the separator between entries in Z. We get (X * Y + 2 + Z) bits for each position. Total (X * Y + 2 + Z) * ​​5 * 10 ^ 20 bits required to allocate to store all the positions used in the initial arrangement.
   
   There is 1TB = 8 * 10 ^ 12 bits available
   It is necessary to develop a compression algorithm for this task, while maintaining fast data indexing.
   
   
3. Let's try to find repetitive patterns in the records and implement the replacement of repeats for shorter records. Ideologically, the algorithm is similar to the Huffman code.
   
   Negative impact on not so fast indexing.
   

Total need to compress data c ≈ 10 ^ 22 to 10 ^ 13 bits. So, it was necessary to write an algorithm that would allow compressing the data by only 99.9999999914163%. I doubt that any algorithm is capable of it, and without taking into account that it is necessary to maintain fast indexing.

Result:

Saving any data on all batches is not applicable at all.

Return to the project only on RAM. Creating a "processor"

It was customary to store data that was stored in files in RAM. To this end, it was decided to change the data storage structure:

 class list_strings { public: list_strings* next; char* data; list_strings() { data = new char[17]; data[0] = '\0'; next = nullptr; } }; class Queue { public: ListCheckers *plch; /*pointer to list of checkers*/ list_strings *pcs; /*list of data of childs*/ chcolor color; chresult result; int to_draw; } 

And also changed the principle of storage of the object Queue. After the MainQueue was overwritten, the Queue object pointed to by the MainQueue is also overwritten.

The “pcs” field for storing “children” is now implemented as a single-linked list with data of the “Aaaaaaaaacaaaaa” type, expanding as necessary. In order to use the allocated memory repeatedly (when overwriting) the fields with data became equal to '\ 0' - zero, to indicate that the fields do not contain important information. Since The “object” has changed.

Result:

Maximum space occupied on RAM: 844 KB. Run at 7 o'clock allowed to see 8.865.798.818 positions. But, positions can be repeated. These results are not sufficient to achieve a complete miscalculation of the party for an acceptable execution time.

Now we can say that there is a “processor” that will grind the positions and it will only need 844 KB of RAM, which means that the remaining memory can be spent usefully, for example, to implement “cache memory” in order not to calculate the positions that have already been calculated .

Creation of "cache memory"

For the fastest possible sampling of data from memory, a hash table was selected that populates the maximum possible memory space. As the hash function, the last numbers of the md5 algorithm were selected, at the input of which the coded position described was fed. That is, the position “Aaauaueaaacckaaa” with md5 0237d0d0b76bcb8872ecc05a455e5dcf will be stored at: f * 2 ^ 12 + c * 2 ^ 8 + d * 2 ^ 4 + 5 = 15 * 4096 + 12 * 256 + 13 * 16 + 5 = 64725.

The unit for storing an entry in a hash table was a cell. This approach allows you to delete data from “obsolete” cells and reuse their space. "Obsolescence" is implemented using a ring buffer:


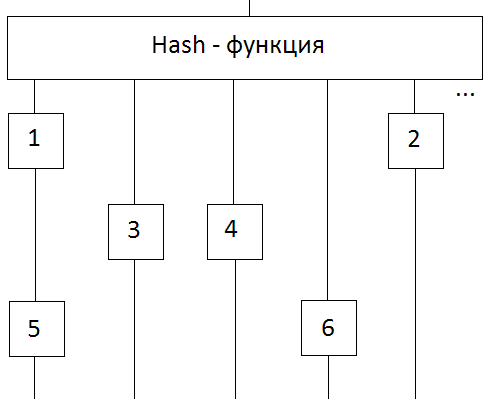
At the first address in the cache-memory cells № 1 and № 5 are stored, in the second № 3 ... And in the circular buffer the cells are stored in chronological order. If we could keep a maximum of 5 cells, then the cell from No. 1 would be “pulled out” from the place where it is now and placed in the place of the 6th cell. Moreover, now only the number 5 cell will be stored in the cache memory at the first address.

 class mem_cel { public: mem_cel* pnhc; /* pointer to next in hash collection */ mem_cel* pphc; /* pointer to prev in hash collection */ mem_cel* pnrb; /* pointer to next "mem_cel" record in ring buffer */ mem_cel* pprb; /* pointer to prev "mem_cel" record in ring buffer */ chresult result; int draw; stringMap condition; }; 

The condition field is necessary to identify the desired checker placement, because different arrangements can be stored at the same cache address.

The draw field is required to determine if the query matches. If there is a drawable result of a position in memory, for which only 3 moves were allocated, then if there are more moves, you can either win or lose.

Result:

Run for 1 hour allowed to see 10.400.590 positions. It is necessary to realize something, allowing to accelerate the given miscalculation. But, if you make calculations, then my computer, at best, will calculate 10 ^ 20 positions in the current: 10 ^ 20 / 10.400.590 = 9.6 * 10 ^ 12 hours = 4 * 10 ^ 11 days.

Let's see which piece of code is “narrow neck”. For this purpose, I used the OProfile profiler:



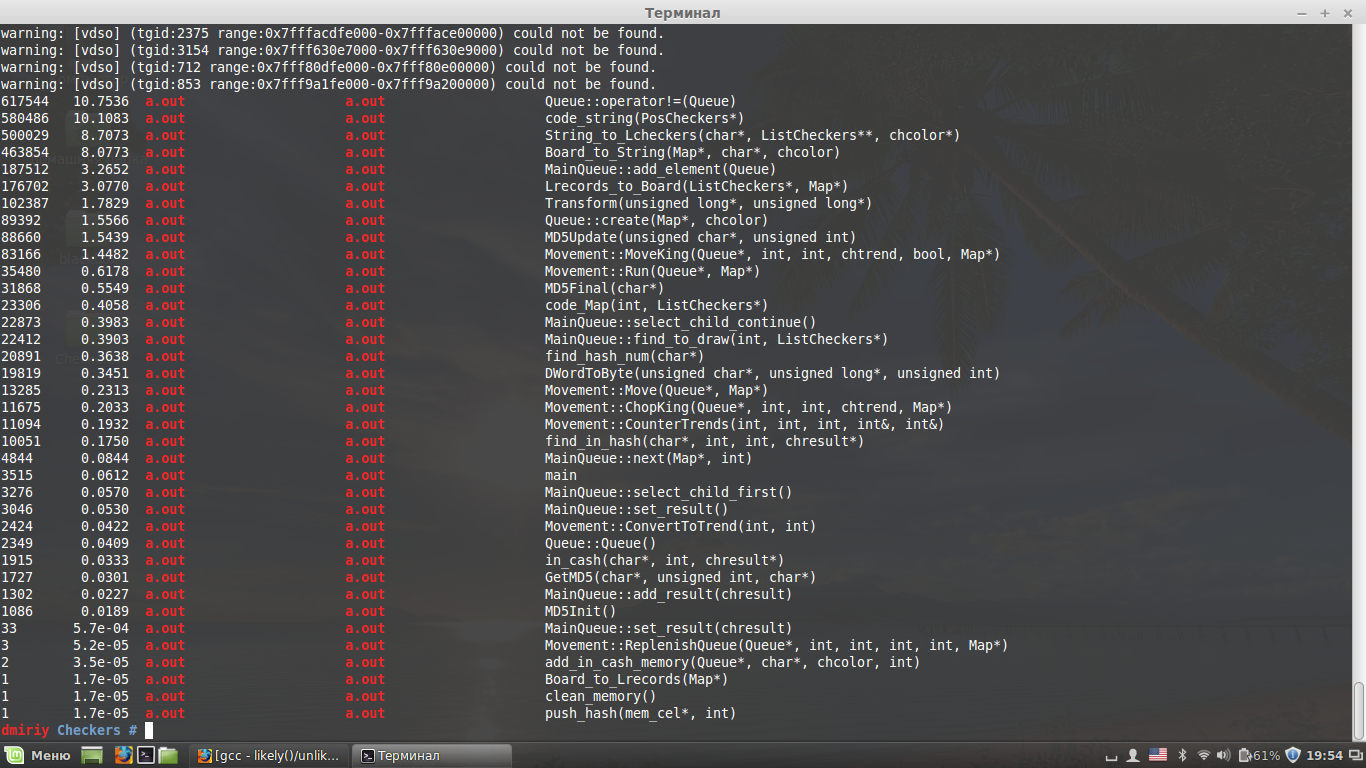
one.

 Queue::operator!=(Queue) 

Check the difference of elements of the queue Called when a new item is added to the queue to check for a triple repetition of a position. The check is performed with all elements that led to the current position.

Optimization: When changing the number of pieces on the board or their status, mark. In order with the positions that have a different set of shapes, do not produce a check.

2

 code_string(PosCheckers*) 

Used to convert a checkpoint element to a letter. Required for the Board_to_String function (Map *, char *, chcolor).

Optimization: First, reduce the number of calls to the Board_to_String function (Map *, char *, chcolor)

3

 String_to_Lcheckers(stringMap, ListCheckers**, chcolor*) 

four.

 Board_to_String(Map*, char*, chcolor) 

Called often enough. So it is necessary to reduce the number of calls to them.
String_to_Lcheckers is needed to convert text into a collection of checker data.
Board_to_String is required to translate a position into text that can be stored in an OP.

Optimization: Since in order to represent the same position on the board I need to work with three data structures:

Lcheckers - a list of checkers on the field. Required for quick selection of checkers to view the possibility of a move. Map or “Board” - array [8] [8]. Contains a complete balance of power.
stringMap or “String” is a string for storing data. It means that you need to reduce the number of conversions from one data view to another, or try to reduce the number of data structures.

Magic bitBoards

Unexpectedly, I found a solution for habrahabr: Magic beatboards and Russian checkers . In which the author of the article proposes to encode information about the board with the help of 4 32-bit words.

The words:

1) the positions of all the figures in white
2) positions of all black pieces
3) white drafts positions
4) the position of the black pieces

Moreover, the positions of the figures are numbered as follows:


Now, to clarify the possibility of cutting at least one checker, it is enough to move the position of all checkers in the appropriate direction:

 bitboard_t try_left_up = ((((checkers & possible_left_up) << 1) & enemy) << 1) & empty; 

Thereby accelerating the search for opportunities, as a felling, and a simple move. To my great regret, I did not understand the author of this article, how he decided to work with the woman. I currently have not beautiful for, which, of course, should be corrected in the future.

Thus, it is possible to replace the 3 data structures described above with one:

 typedef uint32_t bitboard_t; bitboard_t bbMap[4]; 

Also, this change allowed not to use md5 to find the number in the hash-table. This mission was assigned to this formula:

 #define HASH_NUM 0xFFFFFF hash_num = ((bbMap[0] ^ ~bbMap[1]) ^ ReverseBits(~bbMap[2] ^ bbMap[3])) & HASH_NUM; 

Where ReverseBits is a reversal of bits. Example: there was a number 0x80E0, it became 0x0701.

Result:

The launch for 1 hour allowed to view 15.140.000 positions, which is undoubtedly better. But this is still not enough for a complete miscalculation.


I believe that the project algorithm is implemented. Therefore, you can focus on speeding up the functions.

Acceleration of functions

Having read of the likely / unlikely I decided to test its “acceleration” of the code. In general, likely / unlikely indicates which instructions should be loaded by the processor during the execution of an if statement. Either those that are after then, or after else. When an unsuccessful choice of instructions, for example then, the processor is idle, waiting for the instructions specified after else. Under the MS compiler, this instruction is called __assume.

Having implemented each if in this way, I decided to test:

 __assume(selected == nullptr); if (selected != nullptr) { return selected; } 

Result:

To my great surprise, the code has really sped up a lot. During the first hour, 16,750.000 positions were calculated.

I did not dare to implement assembler inserts. My code becomes immediately unreadable, and this is an important aspect for me. Since the breaks in the project, I sometimes reached several months.

The limiter of the number of counted moves into the depths

Unfortunately, it can be called this: over time, I really realized that it’s still impossible to calculate all the positions. Therefore, I added a move limiter with a result function:
checker = +1 point, lady = +3 points. I am aware that this approach is not entirely correct, but for the most part it will produce valid values. So I decided to stop there.

Result:

I went back to where I started. With a limiter on the number of counted moves, my program is currently a program for solving combinational problems. But it's not scary, the limiter can be postponed.

Overall result:

In the first hour, ≈17 million positions are calculated.
What to do next? Unclear.You can use CUDA, parallelize the calculations ... But I don’t think that with this you can achieve a calculation of at least 50 moves for each player on one computer. You would have to know how many positions you have to go through ...

It is necessary to change the algorithm ... How? There are no ideas ... Can use advertised neural networks? I do not think that the neural network will appreciate the loss of checkers at the beginning of the game.

So far I will wait for the coming time of the appearance / cheapening of faster computers. Perhaps, then, more advanced technologies in code acceleration will appear. And while I'm going to study neural networks, maybe I'm wrong and they will be at the head of the computational algorithm ... We will live and see.

Some data:
Maximum depth of rendering - The number of viewed positions
1 - 7
2 - 56 (We make White's first move. Then we generate 7 new positions for black. We look at each of them, make sure we don’t need to calculate further. We make the second move of White ... 7 + 7 * 7)
3 - 267
4 - 1017
5 - 3570
6 - 11 460
7 - 34 455
8 - 95 921
9 - 265 026
10 - 699 718
11 - 1 793 576
12 - 4 352 835
13 - 10 571 175