Can bitcoins be calculated faster, easier or easier?

It all started with the fact that I decided to get acquainted with Bitcoins. I wanted to understand how they are mined. Articles about bitcoins and blockchains are often found recently, but such that with all the technical details, there are not many of them.

The easiest way to understand all the details is to study open source. I undertook to study the Verilog FPGA miner's source code. This is not the only such project, there are a few more examples on github, and all of them, albeit from different authors, seem to work along roughly the same lines. It is possible that the author then all of them was originally the same, just different developers adapt the same code for different chips and different boards ... At least it seemed to me ...

So I, having studied the source code of Verilog, adapted the project with github to the Mars Rover3 board based on the FPGA Altera MAX10, 50 thousand logical elements. I was able to start my miner and even was able to start the process of calculating bitcoins, but I quit this business in half an hour because of the futility. My FPGA miner is too slow in its current times. Well, let.
')
Honestly, in this whole project I was not interested in the Bitcoins themselves (well, they, these money surrogates), but rather the mathematical side of the SHA256 algorithm. That's what I would like to talk about. I have conducted several experiments with the SHA256 algorithm, maybe the results of these experiments will seem interesting to you.

The first thing I needed to do for my experiments was to write a “clean” implementation of SHA256 on Verilog.

In fact, there are many implementations of the SHA256 algorithm in Verilog, at least on the same opencores.org , at least on github.com . However, such implementations are not suitable for me for experiments. Existing modules always have a pipeline structure, pipeline. It would seem - this is correct. Only with the presence of the pipeline, you can get a high speed of the algorithm. The SHA256 algorithm consists of 64 processing steps, the so-called "rounds". If the FPGA volume allows, it is possible to expand all 64 rounds into a single chain of operations: all the computation steps are performed in parallel in one cycle of the operating frequency. Like this:


At the input of the algorithm, eight 32-bit state words of the SHA256 machine. These are registers A, B, C, D, E, F, G, H. The input data itself, 512 bits, will be converted into coefficients W, which are mixed in at each round. While new data words are being loaded into the registers of the first round, the second round continues to read the data loaded at the previous clock cycle, the third round continues to count what was loaded at the previous previous bar, and so on. The final latency, that is, the delay of the result of the calculations will be just 64 clocks, but on the whole the pipeline / pipeline allows you to read the whole algorithm for 1 clock. If the FPGA volume is small and does not allow to expand the whole chain of rounds, then it is shortened by half. This is how it turns out to fit the project into an existing FPGA, but the computational rate naturally drops twice. You can take an even less capacious FPGA and fit it there, but you will still have to shorten the pipeline and performance will suffer again. As I understand it, the whole Bitcoin miner, in which two consecutive SHA256-transforms need about 80 thousand logical elements in Altera / Intel FPGAs. But I was distracted ...

So, I want to do a completely absurd thing - to write on Verilog the “pure” function of the SHA256 algorithm without intermediate registers, to leave it without a pipeline. The goal of this strange action is simple - to determine the actual amount of logic needed to calculate the SHA256 algorithm. I need a simple combination circuit that feeds 512 data bits to the input (well, 256 bits of the initial state) and it gives 256 bits of the result.

I wrote this Verilog module, somewhere I wrote something myself, borrowed something from other open sources. My project is "sha256-test".


Naturally, you need to make sure that the module is working. For this you need a simple testbench to submit to the input of some kind of data block and see the result.


I will compare with the answer that the function sha256_transform gives me, written in the C language (may I not give the C code? These implementations in C / C ++ are full). Main result:



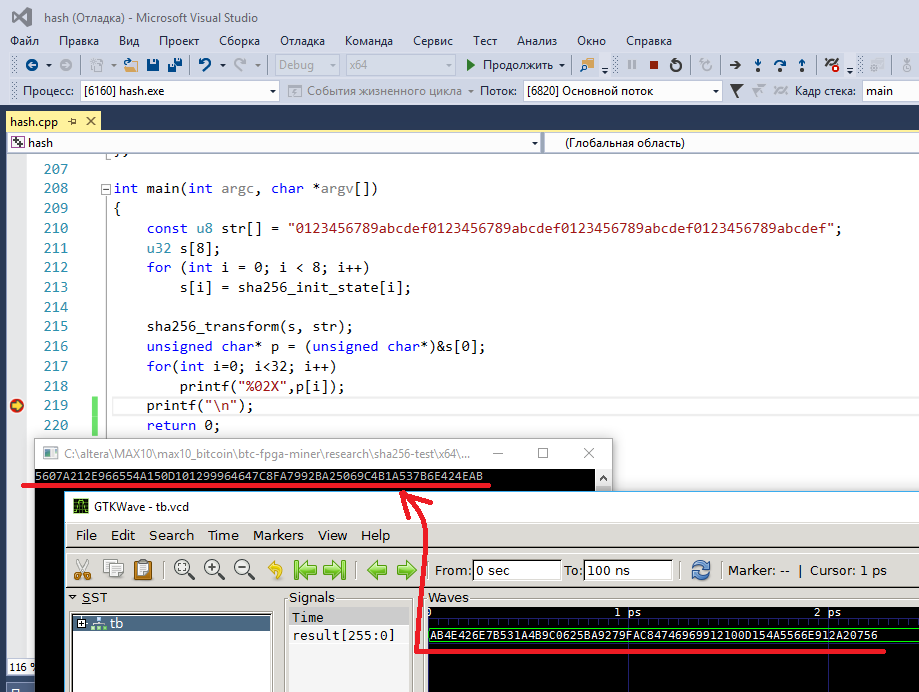
I program in C / C ++ in Visual Studio, and I test Verilog with icarus verilog and gtkwave. I am convinced that the answers are the same, so you can move on.

Now you can insert the module into the FPGA and see how many logical elements such a function can occupy.

We make such a project for FPGA:

 module sha256_test( input wire clk, input wire data, output wire [255:0]result ); reg [511:0]d; always @(posedge clk) d <= { d[510:0],data }; sha256_transform s0( .state_in( 256'h5be0cd191f83d9ab9b05688c510e527fa54ff53a3c6ef372bb67ae856a09e667 ), .data_in( d ), .state_out(result) ); endmodule 

Here it is assumed that the input data is pushed into one long register of 512 bits, which is fed as input to my “clean” SHA256_transform. All 256 output bits are output to the output pin of the FPGA chip.

I compile, for FPGA Cyclone IV, and I see that this thing will take 30,103 gates.
Well remember this number: 30103 ...

Let's do the second experiment. Project "sha256-eliminated".

 module sha256_test( input wire clk, input wire data, output wire [255:0]result ); sha256_transform s0( .state_in( 256'h5be0cd191f83d9ab9b05688c510e527fa54ff53a3c6ef372bb67ae856a09e667 ), .data_in( 512'h66656463626139383736353433323130666564636261393837363534333231306665646362613938373635343332313066656463626139383736353433323130 ), .state_out(result) ); endmodule 

Here, I do not submit input data to the FPGA from the outside, but simply set a constant, constant input signal for the sha256_transform module.

Compile in FPGA. Know how many logical elements will be involved in this case: ZERO .



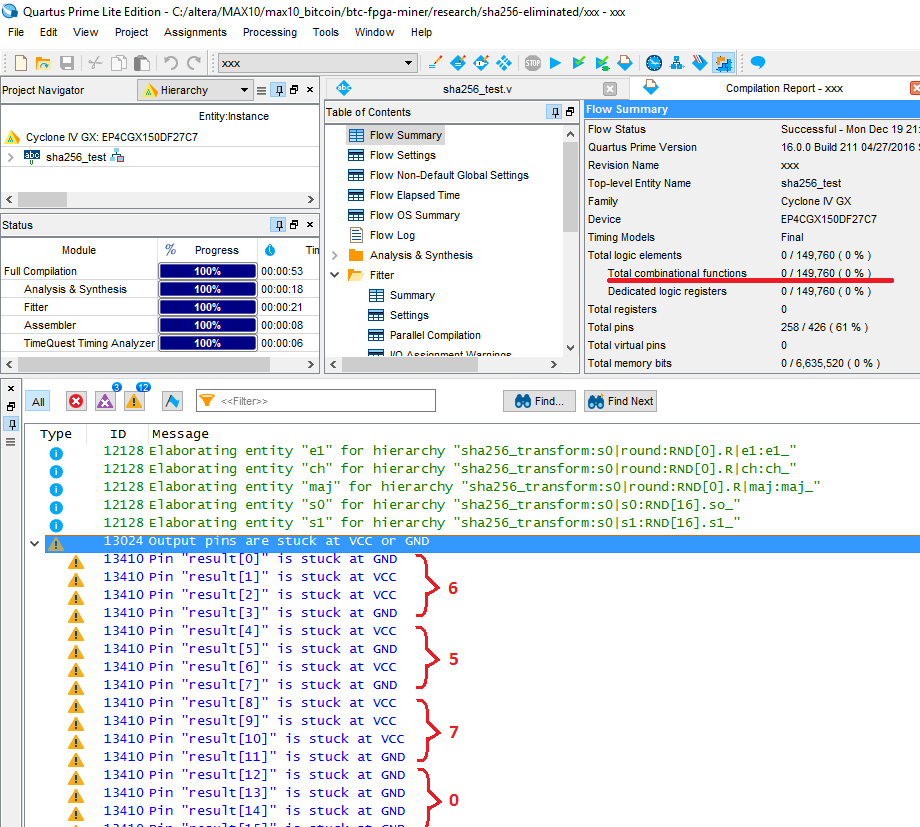
Altera environment (or already Intel? How to call correctly?) Quartus Prime optimizes all the device logic and since there are no registers and no input signals on which the result depended, the whole combinational function degenerates, the input parameters of the SHA256 module are calculated directly during compilation. You can view the output signals on the FPGA pins. The compiler immediately writes that some signals will be attached to the ground, and some to the VCC, to the supply voltage. So the output will be the result calculated by the compiler itself: 0x56, 0x70, ... just like in my very first test example.

This is where the thought comes from. Since the compiler is so smart and can optimize the logic so well, why not consider only one output bit from sha256? How much logic does it take to count only one result bit?

Indeed. Bitcoins are considered like this: there is a data block. In the data block there is a variable field that can be changed - this is a nonce field, 32 bits. The remaining data in the block is fixed. We must change, iterate the nonce field so that the result of sha256 is “special”, namely, that the high bits of the result of sha256-transform turn out to be zero.



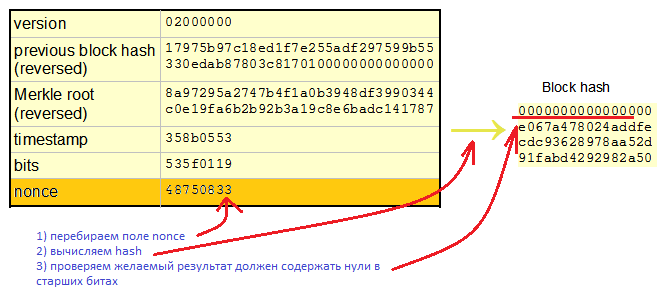
Here we count sha256 once, then we increase nonce by one, again we count hash, then again and again. Hundreds, thousands of times the same data block but a slightly different nonce field. This calculates all the bits of the sha256 result, that is, all the output 256 bits. Is it profitable energetically? Is it beneficial for the number of logic elements involved?

And what if you count only one of the higher bits of the result. He think it is equally likely to be either zero or one. If it turns out to be one, the remaining bits should not be counted. Why waste precious energy on them?

Having made this assumption, for some reason I immediately decided for myself that the number of logical elements for calculating only one bit of a hash should be 256 times less than for calculating all the bits of the result. But I was wrong.

To test this hypothesis, I decided to make a project for a quarter with a top module that looks like this:

 module sha256_test( input wire clk, input wire data, output wire result ); reg [511:0]d; always @(posedge clk) d <= { d[510:0],data }; wire [255:0]r; sha256_transform s0( .state_in( 256'h5be0cd191f83d9ab9b05688c510e527fa54ff53a3c6ef372bb67ae856a09e667 ), .data_in( d ), .state_out(r) ); assign result = r[187]; // ,    endmodule 

Note that sta256_transform seems to compute the entire hash and the response will be in the signal wire [255: 0] r, however, the output of the Verilog module is only one bit, which assign result = r [187]; This will allow the compiler to effectively leave only the logic that is needed to calculate the desired bit. The rest will be optimized and removed from the project.

To conduct my experiment, I just need to fix the last but one line and recompile the project 256 times. To facilitate such work I will write a script for the quarter:

 #!/usr/bin/tclsh proc read_rpt { i frpt } { set fp [open "output_files/xxx.map.summary" r] set file_data [read $fp] close $fp set data [split $file_data "\n"] foreach line $data { set half [split $line ":"] set a [lindex $half 0] set b [lindex $half 1] if { $a == " Total combinational functions " } { puts [format "%d %s" $i $b] puts $frpt [format "%d %s" $i $b] } } } proc gen_sha256_src { i } { set fo [open "sha256_test.v" "w"] puts $fo "module sha256_test(" puts $fo " input wire clk," puts $fo " input wire data," puts $fo " output wire result" puts $fo ");" puts $fo "" puts $fo "reg \[511:0]d;" puts $fo "always @(posedge clk)" puts $fo " d <= { d\[510:0],data };" puts $fo "" puts $fo "wire \[255:0]r;" puts $fo "sha256_transform s0(" puts $fo " .state_in( 256'h5be0cd191f83d9ab9b05688c510e527fa54ff53a3c6ef372bb67ae856a09e667 )," puts $fo " .data_in( d )," puts $fo " .state_out(r)" puts $fo " );" puts $fo "" puts $fo "assign result = r\[$i];" puts $fo "" puts $fo "endmodule" close $fo } set frpt [open "rpt.txt" "w"] for {set i 0} {$i < 256} {incr i} { gen_sha256_src $i exec x.bat read_rpt $i $frpt } close $frpt exit 

This script re-creates the sha256_test.v module in the loop and each time outputs the next sha256 result to the output FPGA pin.

I run the script for a couple of hours and voila. There is a table of values. Now we know exactly which bit from SHA256 is the easiest to calculate. Here is a graph of the required number of logical elements of the sequence number of the calculated SHA256 bit:



From here it becomes clear that it is easiest to calculate bit number 224. It requires 27204 logical elements. This is actually almost 10% less than when calculating all 256 output bits.

The graph in the form of a saw is explained by the fact that there are many adders in the SHA256 algorithm. In the adder, each next most significant bit is more difficult to calculate than the previous one. This is due to the transfer scheme, because adders consist of many full-adder blocks.

Ghostly energy savings have already appeared. I believe that every logical function eats energy. The smaller the number of involved logical elements LE in the FPGA project, the lower the energy consumption. The proposed algorithm is as follows: we consider one of the simplest bits, if it is zero, then we consider the following. If it is one, then we do not spend energy and time and energy on the remaining bits in the same hash.

Now another thought, also related to the compiler's capabilities to optimize the logic.

Since when searching the nonce field, the main data of the block remains the same, it is logical and obvious that from cycle to cycle some calculations simply repeat and consider the same thing. Question: how to estimate how much energy is lost there on repeated calculations?

The experiment is simple. For example, we put two sha256_transform modules side by side and feed them with the same input data, well, except for one bit. We believe that these two modules consider neighboring nonce differing in one bit.

 module sha256_test( input wire clk, input wire data, output wire [1:0]result ); reg [511:0]d; always @(posedge clk) d <= { d[510:0],data }; wire [255:0]r0; sha256_transform s0( .state_in( 256'h5be0cd191f83d9ab9b05688c510e527fa54ff53a3c6ef372bb67ae856a09e667 ), .data_in( { 1'b0, d[510:0] } ), .state_out(r0) ); wire [255:0]r1; sha256_transform s1( .state_in( 256'h5be0cd191f83d9ab9b05688c510e527fa54ff53a3c6ef372bb67ae856a09e667 ), .data_in( { 1'b1, d[510:0] } ), .state_out(r1) ); assign result = { r0[224], r1[224] }; endmodule 

Each of the modules s0 and s1 consider their hash from the same input data, only differ by one nonce bit. From each I take only the “easiest” bit of the result, bit number 224.
How much will such logic take in FPGA? 47.805 logical elements. Since there are two modules, one takes 47805/2 = 23902. It turns out that starting to count two hashes at once is much more profitable than counting them in turn due to the fact that there are general calculations.

And if you start counting at once 4 hashes and only 2 bits of different nonce fields? It turns out 89009LE / 4 = 22252 LE / SHA256

And if you count 8 hashes? It turns out 171418LE / 8 = 21427 LE / SHA256

Here you can compare the original number of 30103 logical elements on the full SHA256_transform with the output of 256 bits of the result and 21427 logical elements on the SHA256_transfrom with the output of one bit of the result (which can be used to predict the appropriateness of further calculations). It seems to me that such methods can reduce the energy consumption of the miner somewhere by almost a third. Well, a quarter ... I do not know how significant it is, but it seems that it is significant.

There is another thought. The main data in the block for calculation remain fixed and only the nonce field changes during the calculation of the hash. If it were possible to quickly compile for the FPGA, then a significant part of the predictions could be performed at the compilation stage. After all, I showed above how effectively the compiler calculates everything that can be calculated in advance. Optimized logic with precalculations will be much or much smaller in volume than is required for a full calculator, hence, it will consume less energy.

Somehow like this. In fact, I myself am not completely sure of my research. Maybe I do not take into account something or do not understand. The proposed methods, of course, do not give a global breakthrough, but something that can save. While this is all rather theoretical reasoning. For the practical implementation of the "pure" SHA256 is not suitable - it will have too small a working frequency. Enter the pipeline necessarily have to.

There is another factor. In real life, two consecutive SHA256_transforms are counted for Bitcoin. In this case, my estimated gain in terms of the number of logical elements and the energy consumed will probably be not so significant.

Sources of the bitcon miner project for the Mars Rover 3 board with FPGA Altera MAX10, 50K LE here . Here in the research folder there are all the sources of my experiments with the SHA256 algorithm.

Description of the project miner for FPGA here