Non-computable functions on the example of the Busy Beaver Game

Computers have penetrated most areas of human life and continue to evolve. Autopilot, banking, machine translation, medicine, financial markets, flights into space - all this is possible thanks to one simple idea.

In this article, I propose to look beyond the boundaries of the capabilities of computers and consider what they can not. And why. Alan Turing back in the 30s identified impossible tasks for a computer.

Turing Machine

To be extremely precise, the very same Turing publication, which laid the foundation for computer science [1], was precisely about computable functions, which emphasizes the existence of a boundary that the Turing machine cannot step over.

A Turing machine (MT) is an abstract computer that is closely related to the concept of an algorithm [10]. This is the easiest computer.

It is also worth remembering that any function that can be calculated by a physical device can be calculated by a Turing machine [2]. This leads to the fact that all conclusions concerning the abstract Turing machine are fully applicable to any computers on any architecture.

Incomprehensible functions and stopping problem

The problem of stopping [3] can be formulated as: there is no general algorithm that could determine whether the program will stop, according to its description and input data.
Those. the stop definition function is not computable. Evidence can be found on Wikipedia.

In practice, it looks like this - the computer itself will never be able to determine for sure whether its next program will hang in an endless stream of instructions or not. But after all, programs written by man are not perfect.

One known attempt to solve this problem arose in the depths of Microsoft called Microsoft Terminator [4]. Microsoft wanted to reduce the number of buggy drivers to hardware by building an automatic system for checking their correctness. They tried to build a tool to prove the correctness of the mathematical model of the program. I do not know about the positive results, but I think they managed to partially increase the stability of the drivers.

Busy beaver game

In 1962, this problem was identified by the Hungarian mathematician Tiber Rado, in the article "On non-computable functions" [5]. Using the analogy of the beaver, he explained the Turing machine, but the name stuck. Even in this article, the largest number known at that time was mentioned.

If you limit the Turing machine (MT) to N states, then you can create a finite number of machines.
With an increase in the number of states N, the number of possible Turing machines grows faster than exponentially: (4 (n + 1)) ^ 2n.

Among the remaining MT there will be two types - those that stop and not.

Rado asked one question in two formulations:

• What is the maximum number of operations can make MT with N states before its completion. This is called the Busy Beaver number, denoted as BB (n) or S (n).
  
• What is the maximum number of units that can print MT with N on an empty tape to completion. It is denoted as Σ (n).
  

Obviously, this number exists. And having counted it, it would be possible to check whether the MT is completed in this number of steps. If not, it is obvious that it will work forever, since the maximum threshold is passed.

The Busy Beaver Game offers to find a program for a Turing machine with N states that runs as long as possible and then ends.

As input, the tape of the Turing machine is filled with zeros.
You need to create a program that fills it with the maximum number of units and ends by going into the HALT state.

Here are the rules for a two-state Turing machine (N = 2). The same example is the Busy Beaver solution for N = 2.

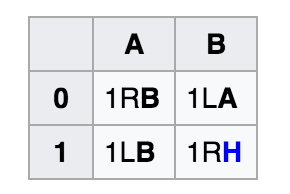
Program execution goes something like this:

• The entire tape is filled with zeros as input.
• The initial state is A.
• We read the current bit - if it is 1, then we execute code A1, otherwise - A0.
• Instructions 1RB mean - write on summer 1, go to the right, go to state B.
• The program continues until the transition to the state of HALT (H)

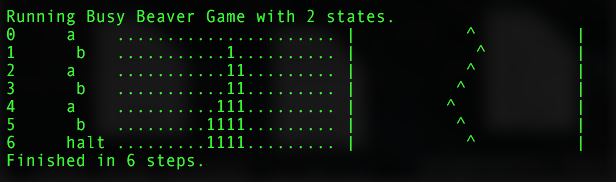
Figure 1. Visualization of the step-by-step MT operation with N = 2. The first column is the step number. The second column shows how MT states change as you progress. The third column is the tape status, where you can see the order in which units appear on it. The fourth is the trajectory of moving the pointer on the tape.

N = 3

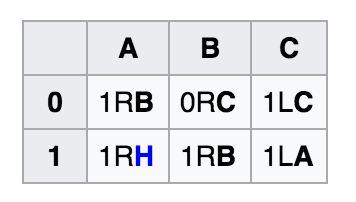
Figure 2. Busy Beaver solution for task N = 3

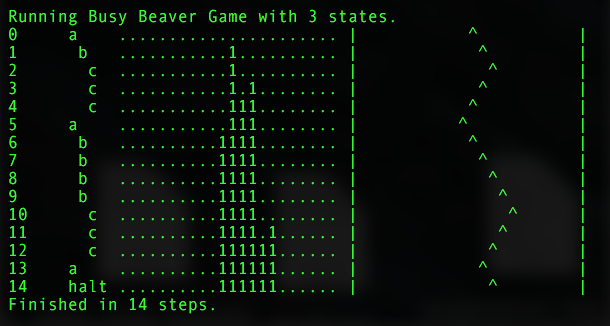
Figure 3. Visualization of the step-by-step MT operation with N = 3.

N = 4

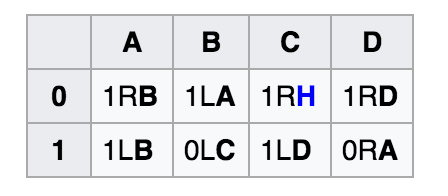
Figure 4. Busy Beaver solution for N = 4

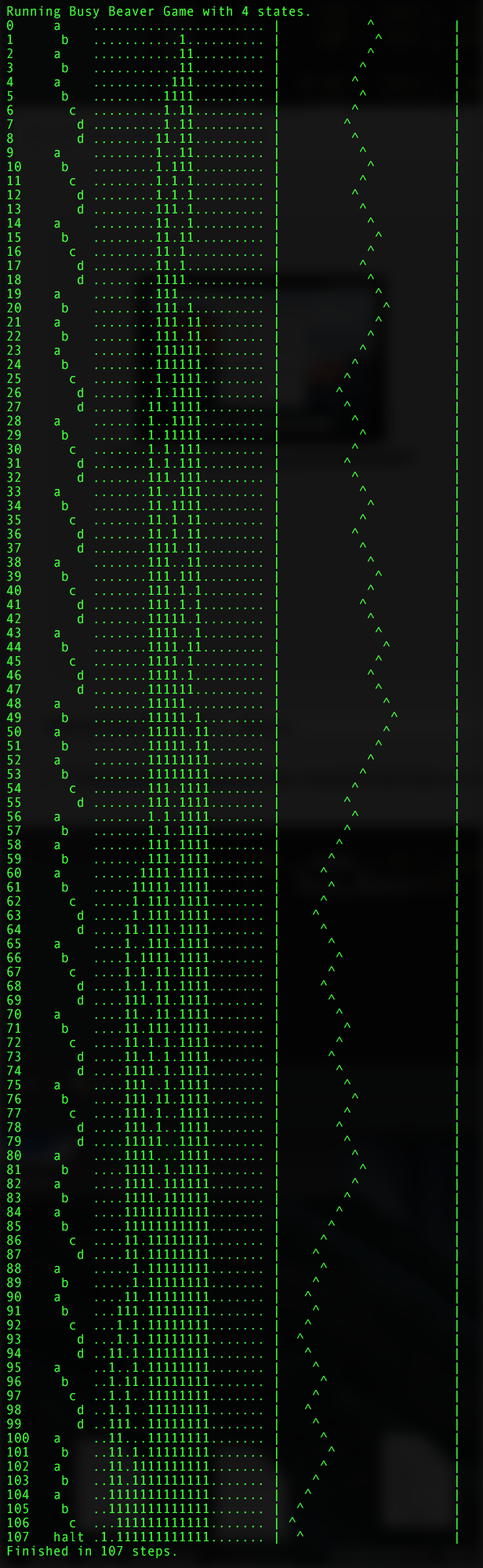
Figure 5. Visualization of the step-by-step MT operation with N = 4. Here is a Christmas tree, with the coming!

To display such a graph N = 5, we would need 47,176,870 steps minimum.
When N = 6, the maximum number of the Beaver found today is S (6) = 7.4 × 10 ^ 36534.
For N = 7, there is only a preliminary estimate of S (7)> ​​Σ (7)> ​​10 ^ 10 ^ 10 ^ 10 ^ 18705352 [6]

Today, it is believed that people can find S (6) and provide evidence that it is maximum. S (7) is absolutely unavailable [8].

There are various variations: 3,4,5,6 characters can be written to the tape, instead of {0,1}. In this case, the numbers only grow.

How to solve this problem?

The general approach to the solution looks like the division of all possible Turing machines into the following classes:

• Tree-normalized : these machines are excluded from the search space, because it is proven that they are equivalent to other MTs or their behavior is obvious [8]
• Candidate-halter : Machines that are guaranteed to stay are candidates for the title Busy Beaver Game champions.
• Non-candidate-halter : stopping, but not satisfying certain requirements.
• Non-halter : many small classes for each of which exhibits a specific behavior associated with not stopping.
• Holdouts : all that remains is not clear whether or not these machines stop. When this class is empty, the Busy Beaver problem can be considered solved.

With the help of tree normalization, tree MT can be significantly reduced.

• An example of the tree normalization method is the removal of half of the MT, where the first step is taken to the left. Because there is a similar mirror machine, which starts moving to the right [8]. *

Supertreaming computations

If we were able to build a machine for calculating BB (n), it would have been an extra-clearing machine.
Overtringing computations are computations that cannot be done on a Turing machine [9]. But is it possible to build a physical super-tuning computer [7]?

An important question for creating Strong Artificial Intelligence is whether the human mind operates only with turing calculations?

Conclusion

Why try to solve an unsolvable problem? Maybe because the boundary cases in mathematics reveal the fullness of the original theory.

The Busy Beaver Game is closely related to the theory of computability, the problem of stopping and the theory of complexity.

This task also made me think - what could a Turing machine calculate for a little less than infinity?

My blog on Medium

Links

[1] On Computable Numbers
[2] Church-Turing Thesis
[3] Stop Problem
[4] Microsoft Terminator
[5] On non-computable functions
[6] Good bound for S (7)
[7] Hypercomputation: Hype or Computation?
[8] The complex behavior of simple machines. Rona machilin
[9] Supertching calculations
[10] Turing Machine
[11] Python and C ++ sources by Peteris Krumins