Lock-free data structures. Iterable list

The lock-free list is the basis of many interesting data structures, the simplest hash map , where the lock-free list is used as a collision list, the split-ordered list , built entirely on the list with the original splitting algorithm of the bucket, a multi-level skip list that is essentially hierarchical list of lists. In the previous article, we made sure that you can give such an internal structure to a competitive container so that it supports thread-safe iterators in the dynamic world of lock-free containers. As we found out, the main condition for the lock-free container to become iterable is the stability of the internal structure: nodes should not be physically deleted (delete). In this case, the iterator is simply a (possibly composite) pointer to a node with the possibility of moving to the next (increment operator).

Can this approach be extended to the lock-free list? .. Let's see ...

A regular lock-free list has the following node structure:

template <typename T> struct list_node { std::atomic<list_node*> next_; T data_; }; 

In it, the data is incorporated directly into the node, therefore, deleting the key (data) results in the deletion of the entire node.
')
Separate the node and the data - let the node contain a pointer to the data that it carries:

 template <typename T> struct node { std::atomic<node*> next_; std::atomic<T*> data_; }; 

Then, to delete the key, it is enough to reset the data_ field of the node. As a result, our list will acquire the following internal structure: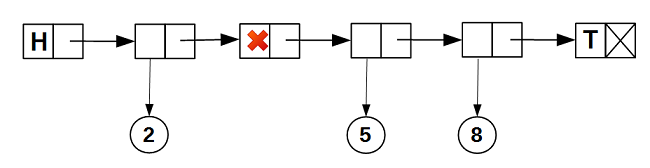



Nodes are never deleted, so the list is iterable: the iterator is actually a pointer to the node:

 template <typename T> struct iterator { guarded_ptr<T> gp_; node* node_; T* operator ->() { return gp_.ptr; } iterator& operator++() { //    ,   node_, //      } }; 

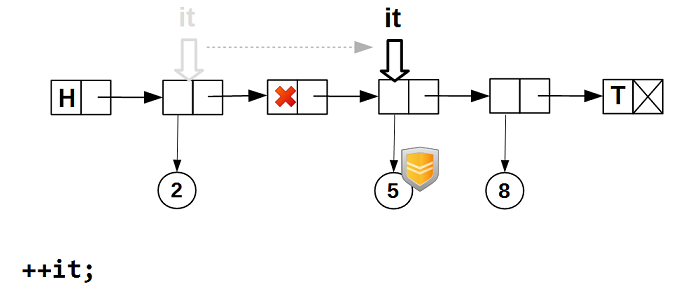
The presence of guarded_ptr (which contains a pointer to data protected by a hazard pointer) is mandatory, since we cannot guarantee that another stream will not delete data for which the iterator is positioned. It is possible to guarantee only that at the time of the iterator's transition to the node_ it (the node) contained data. The protected pointer ensures that while the iterator is on node_ , its data will not be physically deleted (delete).

Let's see in pictures how it works. We start bypassing the list - the iterator is positioned on the first node with non-empty data:



Next, increment the iterator - it skips the nodes with empty data:



Even if some other thread deletes the data of the node where the iterator is positioned, the guarded_ptr iterator guarantees that the data will not be physically deleted while the iterator is on the node: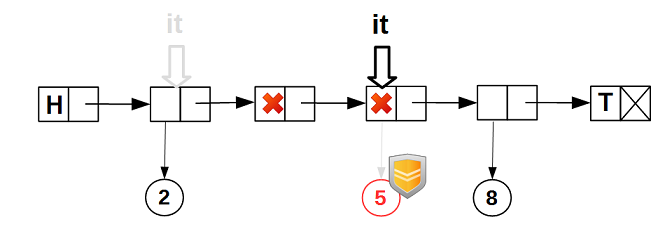



It is possible that the data will be removed from the list, and then other data will be assigned to the same node_ . In this case, the iterator is positioned on the node node_ . It would be strange if in this case operator ->() iterator returned a pointer to different data. guarded_ptr guarantees us the immutability of the data returned by the iterator, but does not at all prevent them from being changed by other threads: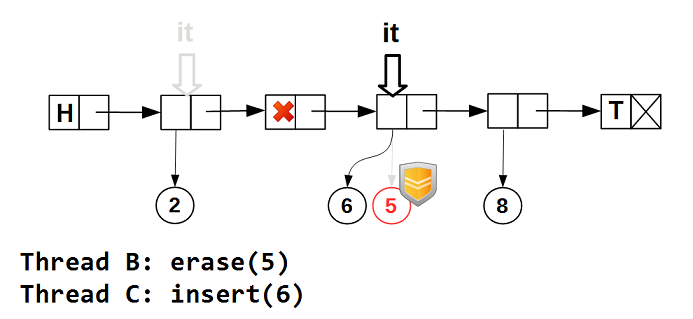



As we see, the constructed iterable list supports thread-safe iterators and has a very simple operation of deleting a key (data), which is reduced simply to zeroing (using the CAS primitive) of the data_ node field. The insert() operation of adding new data is somewhat more complicated, since two cases are possible:

- insert a new node between existing nodes of the list with non-empty data:



This node insertion algorithm is already familiar to us from one of the previous articles.

- setting the data_ field to the empty prev node:



This would end the article, if the second case - reusing empty data_ - would not have thrown a couple of surprises.

First surprise

The first (naive) version of the insert in the iterable list looked like this:



The linear_search function is an ordinary linear search in the list (well, not quite normal, we still have a competitive list, so we are provided with squats with atomic operations and hazard pointers), returns true if the key is found and false otherwise . The out-parameter of the pos function (of type insert_pos ) is always filled. The search stops as soon as the key of the not less sought data . We are interested in inserting a search failure — in this case, the pos will contain the insertion position. The pos.cur node pos.cur always be non-empty (or it will point to the end of the list — a dedicated tail node), but pos.prev — the previous one for pos.cur — may indicate an empty node — this is the case we are particularly interested in. The prevData and curData fields of the prevData structure are the insert_pos values ​​for prev and cur respectively. Note also that we do not need to protect pointers to the prev and cur hazard pointer nodes, since the nodes from our list are never deleted. But the data can be deleted, so we protect them.

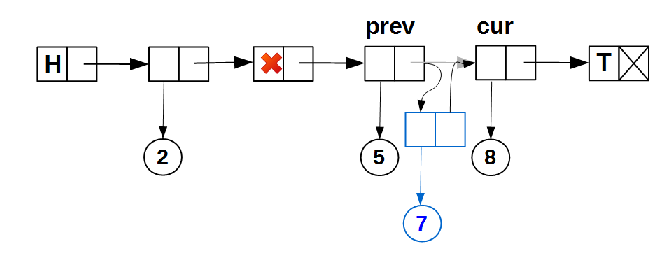
So, the naive implementation simply checks: if the previous node is empty ( pos.prevData == nullptr ), then we try to write a link to the inserted data into it. Since our list is competitive (moreover, until it is even lock-free, but we will fix it soon), we change the pointer prev.data_ atomic CAS: if it is successful, it means that no other stream prevented us and we inserted new data to list.

Here we have the first surprise. Suppose thread A adds a key to the list: linear_search() executed, the insert_pos structure is initialized by the insert position, and the thread is ready to call link() , but then its time has passed and it 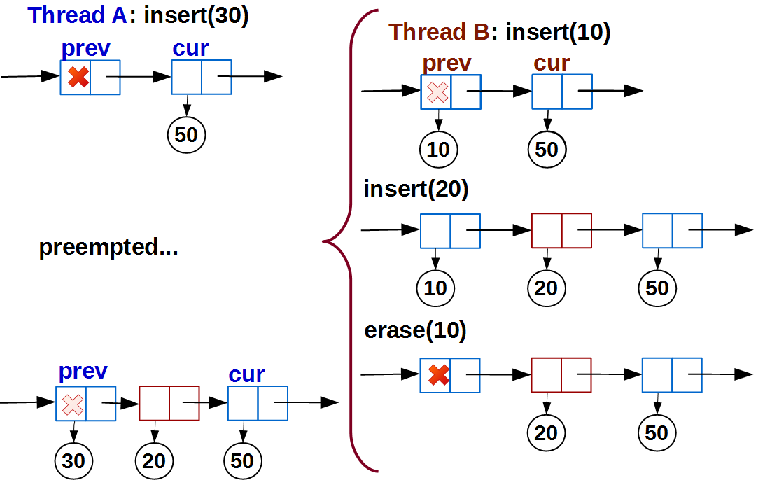became a pumpkin and was replaced by the operating system. At this time, stream B is working with the list:



At the time of the resumption of flow A, the list has changed beyond recognition, but from the point of view of the position found pos flow A, nothing has changed: prev was empty, so empty and remained. Therefore, flow A will write data with key 30 to prev and successfully complete the insertion, thereby breaking the orderliness of the list.

This is a kind of ABA-problem that cannot be solved by using hazard pointers, since the pointer prev->data_ is NULL . We have the right to link new data to an empty node only when the prev -> cur bundle has not changed after the search; moreover, the data of these nodes have not changed. To solve this problem, use the marked pointer technique: the lower bit of the pointer to the node data will be used as a sign of “inserting a new node”. Moreover, it is necessary to mark both nodes — prev and cur — otherwise the other stream may delete data from cur and the list’s orderliness will again be broken (let's not forget that the cur node is always non-empty). As a result, the node structure will change and the link() function of adding data will look like

 template <typename T> struct node { std::atomic< node * > next_; std::atomic< marked_ptr< T, 1 >> data_; }; bool link( insert_pos& pos, T& data ) { //   prev  cur if ( !pos.cur->data_.CAS( marked_ptr(pos.curData, 0), marked_ptr(pos.curData, 1))) { //   — -     return false; } if ( !pos.prev->data_.CAS( marked_ptr(pos.prevData, 0), marked_ptr(pos.prevData, 1))) { //   —    //     pos.cur->data_.store( marked_ptr(pos.curData, 0)); return false; } // ,   prev -> cur   if ( pos.prev->next_.load() != pos.cur ) { // -   -   prev  cur pos.prev->data_.store( marked_ptr(pos.prevData, 0)); pos.cur->data_.store( marked_ptr( pos.curData, 0)); return false; } //   ,   if ( pos.prevData == nullptr ) { //       //  ,    store bool ok = pos.prev->data_.CAS( marked_ptr( nullptr, 1 ), marked_ptr( &data, 0 )); //    cur pos.cur->data_.store( marked_ptr( pos.curData, 0)); return ok; } else { //    —  Harris/Michael //    //        } } 

The introduction of the marked pointer also affects the data deletion function (which, as we recall, comes down to simply zeroing the data_ field): now we have to zero only unmarked data, but this does not add to the complexity of the deletion procedure. Search the list completely ignores our marker.

As a result, the iterable list ceased to be lock-free: if the thread marked at least one of the nodes, and then was killed (there is nowhere to appear in the link() function), the lock-free condition is broken, as the node will remain marked forever and someday will lead to endless active waiting for a tag to be removed. On the other hand, it is a sinful practice to kill streams while working, so I don’t see any particular risks here.

Surprise Two

Unfortunately, testing has shown that this is not a complete solution. If a naive iterable list often showed a violation of data sorting and even in a debug build, then after introducing marked pointers, tests began to show a violation very rarely and only in a release build. This is a signal that we have a very unpleasant problem, practically not reproduced in a reasonable time and can only be solved analytically.

As the analysis showed, the problem is actually orthogonal to the first:



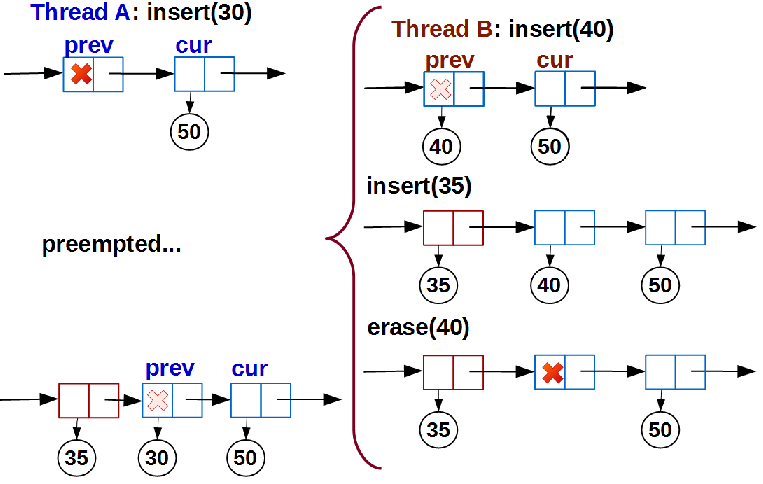
As in the first case, stream A is pushed out before entering link() . While A is waiting for it to be re-scheduled, other threads have time to fool over the list with a sequence of additions / deletions that do not violate the preconditions of the link() function of flow A, but lead to a violation of the list sortedness.

The solution is to add another condition to link() : after we have marked the prev and cur nodes, between which we have to insert a new one (or use an empty prev ), we must check that the insertion position has not changed . This can be checked in the only way - to find the node following the new data, and make sure that it is equal to cur :

 bool link( insert_pos& pos, T& data ) { //   prev  cur // ...    // ,   prev -> cur   // ...    // ,      if ( find_next( data ) != pos.cur ) { // oops!   … pos.prev->data_.store( marked_ptr(pos.prevData, 0)); pos.cur->data_.store( marked_ptr( pos.curData, 0)); return false; } //   ,   // ...    } 

Here, the auxiliary function find_next() searches for the node closest to data .

Conclusion

Thus, an iterative competitive list can be built. Search in it is lock-free, but the insertion and, as a result, the deletion of it is not lock-free. Why is he needed? ..

First, the presence of thread-safe iterators in some problems is important. Secondly, this list is interesting in that the operation of deleting a key in it is much easier than inserting; it suffices to zero the pointer to the data at the node; usually the removal is much harder, see two-phase removal from the classic lock-free list. Finally, this task was for me personally a kind of challenge, since before that I considered the concept of iterators in principle impossible for competitive containers.

I hope that this algorithm will be useful, for an implementation, see the libcds : MichaelSet / Map and SplitListSet / Map based on IterableList with support for thread-safe iterators.