Today we have the most pre-New Year series about FPGAs and the Frankie debug board. Previous series 1 , 2 .

We have already transmitted tones on the radio with our Frankenstein board. Now let's try to play sounds and music.

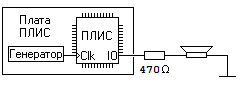
To do this, we connect a regular speaker to the FPGA. A generator at 25.175 MHz is connected to Frankie. If we divide this frequency to the range of audible frequencies and submit it to the output of the FPGA, then we can hear the sound. Me frequency we can get different sounds.

Testing the sound quality will be the best listener in the house - Masha. The frequency range of 60 kHz - this is not a joke! )))

Wiring diagram

To reproduce the sound, I use the speaker from the Designer Connoisseur (I did not find another on the move). The speaker is connected to the output of the FPGA through a resistor with a resistance of 470 Ohms.

Simplest sound

In the FPGA, binary counters fit easily. Therefore, even Frankie will cope with this task. For example, a 16-bit counter will count from 0 to 65535. With our 25.175 MHz and 16-bit counter, we can get sound with a frequency of 25175000/65536 = 384.14 Hz

module epm7064_test(clk, audio); input wire clk; output wire audio; //    16  reg [15:0] counter; always @(posedge clk) counter <= counter+1; //       assign audio = counter[15]; endmodule 

Note "LA" of the first octave (440 Hz)

We got a random frequency in the sound range. Now you can try to get a frequency equal to 440 Hz. This is the frequency of the note "LA" of the first octave.

To do this, instead of dividing the clock frequency by 65536, we must divide the frequency of the clock generator by 57,216 (27,175,000 Hz / 440 Hz).

 module epm7064_test(clk, audio); input wire clk; output wire audio; //    16  reg [15:0] counter; initial counter <= 16'd0; always @(posedge clk) begin if(counter==57216) begin counter <= 0; end else begin counter <= counter + 1'b1; end end assign audio = counter[15]; endmodule 

But there is a problem with this implementation. Although the frequency is 440 Hz, the signal's duty cycle is not equal to 50%. The low level is displayed at the counter values ​​from 0 to 32767, and the high from 32767 to 56817. It turns out that the speaker is in the unit only 42% of the time. The easiest way to get a 50% duty cycle is to add another division by two. That is, first at 28608, and then at 2 more.

 module epm7064_test(clk, audio); input wire clk; output audio; //    15  reg [14:0] counter; initial counter <= 15'd0; always @(posedge clk) begin if(counter==28608) begin counter <= 0; end else begin counter <= counter + 1'b1; end end reg audio; always @(posedge clk) if(counter==28608) audio <= ~audio; endmodule 

Of course, at the hearing it is almost not distinguishable.

To make the code more flexible, you can add the clkdivider parameter. Changing the direction of the account in the counter to the opposite is just a matter of preference. There will be no difference in the used FPGA resources.

 module epm7064_test(clk, audio); input wire clk; output audio; parameter clkdivider = 25175000/440/2; reg [14:0] counter; initial counter <= 15'd0; always @(posedge clk) begin if(counter==0) begin counter <= clkdivider - 1'b1; end else begin counter <= counter - 1'b1; end end reg audio; always @(posedge clk) if(counter==0) audio <= ~audio; endmodule 

Ambulance Siren

Now let's try alternating two different tones. For this we use

the counter (let's call it tone) on 24 bits, for receiving frequency about 1.5 Hz.

This signal will be used to switch between the two frequencies.

 module epm7064_test(clk, audio); input wire clk; output audio; parameter clkdivider = 25175000/440/2; reg [14:0] counter; initial counter <= 15'd0; reg [23:0] tone; initial tone <= 24'd0; always @(posedge clk) tone <= tone+1; always @(posedge clk) begin if(counter==0) begin counter <= (tone[23] ? clkdivider-1 : clkdivider/2-1); end else begin counter <= counter - 1'b1; end end reg audio; always @(posedge clk) if(counter==0) audio <= ~audio; endmodule 

Now let's try to make a police siren. First, let's change the tone counter so that it only has 23 bits to double the frequency (the high bit will change with a frequency of about 3 Hz).

And now you need to come up with a trick to get a "saw". Take bits 15 through 21 from the tone counter. It will look like this: tone[21:15] . These 7 bits will give us a value from 0 to 127, which will grow at a certain speed. As soon as the value reaches 127, it will reset to 0 and begin to grow again. In order to get a decreasing value, we can invert these bits. It will look like this: (~tone[21:15]) . This will give values ​​that go down from 127 to 0, and then everything repeats.

In order to get a saw that gradually increases, and then gradually decreases,

take the bit tone[22] .

 wire [6:0] ramp = (tone[22] ? tone[21:15] : ~tone[21:15]); //   ,  // "if tone[22]=1 then ramp=tone[21:15] else ramp=~tone[21:15]" 

But such a saw is not yet ready for use in our project.

The value of the saw varies from 7'b0000000 to 7'b1111111 . In order to get the values ​​from which one could already get the sound, we will add another 2 bits '01' to the word of the saw value to the left and six bits to the '000000' right.

 wire [14:0] clkdivider = {2'b01, ramp, 6'b000000}; 

Thus, we will receive the constantly changing clkdivider value in the range from 15'b010000000000000 to 15'b011111111000000 , or in a hexadecimal system from 15'h2000 to 15'h3FC0 , or in decimal 8192 to 16320. At a frequency of 25.175 MHz, we will receive a siren sound from 771 Hz to 1537 Hz.

 module epm7064_test(clk, audio); input wire clk; output audio; reg [14:0] counter; initial counter <= 15'd0; reg [23:0] tone; initial tone <= 24'd0; always @(posedge clk) tone <= tone+1; wire [6:0] ramp = (tone[22] ? tone[21:15] : ~tone[21:15]); wire [14:0] clkdivider = {2'b01, ramp, 6'b000000}; always @(posedge clk) begin if(counter==0) begin counter <= clkdivider; end else begin counter <= counter - 1'b1; end end reg audio; always @(posedge clk) if(counter==0) audio <= ~audio; endmodule 

And we got a quick siren. But the real siren changes its speed from fast to slow. We can take bits of tone[21:15] for a fast saw, and bits of tone[24:18] for a saw with a lower frequency.

 wire [6:0] fastsweep = (tone[22] ? tone[21:15] : ~tone[21:15]); wire [6:0] slowsweep = (tone[25] ? tone[24:18] : ~tone[24:18]); wire [14:0] clkdivider = {2'b01, (tone[27] ? slowsweep : fastsweep), 6'b000000}; 

To do this, you need to increase the bit counter tone.

 module epm7064_test(clk, audio); input wire clk; output audio; reg [14:0] counter; initial counter <= 15'd0; reg [27:0] tone; initial tone <= 28'd0; always @(posedge clk) tone <= tone+1; wire [6:0] ramp = (tone[22] ? tone[21:15] : ~tone[21:15]); wire [6:0] fastsweep = (tone[22] ? tone[21:15] : ~tone[21:15]); wire [6:0] slowsweep = (tone[25] ? tone[24:18] : ~tone[24:18]); wire [14:0] clkdivider = {2'b01, (tone[27] ? slowsweep : fastsweep), 6'b000000}; always @(posedge clk) begin if(counter==0) begin counter <= clkdivider; end else begin counter <= counter - 1'b1; end end reg audio; always @(posedge clk) if(counter==0) audio <= ~audio; endmodule 

Playing a melody

And now, in honor of the upcoming new year, let's try to play a song about the Christmas tree. Let's look for notes and videos to understand how this song is played.

In order to play a sequence of notes, we need to create a sequencer that will produce the number of the desired note at the right time. We will convert this note value to a constant for the frequency divider to get the corresponding note.

Judging by the video, we need only one octave + 1. In principle, we don’t need all the notes.

And you need only 7 notes that are used in the song. Therefore, 3 bits are enough to store the note number. It would be more correct, of course, to say not the note number, but the number of the tone or frequency in the melody.

So, we have notes in the melody: do, re, mi, fa, salt, la and until the next octave. We number them accordingly. The sequence is as follows:

  5   3 3  5   3 3      5 4 3 2 1  (+1)          

I will draw a temporary chart.

Using a secret tabular processor, we calculate the frequencies of notes and the values ​​of dividers, slightly rounding them out.

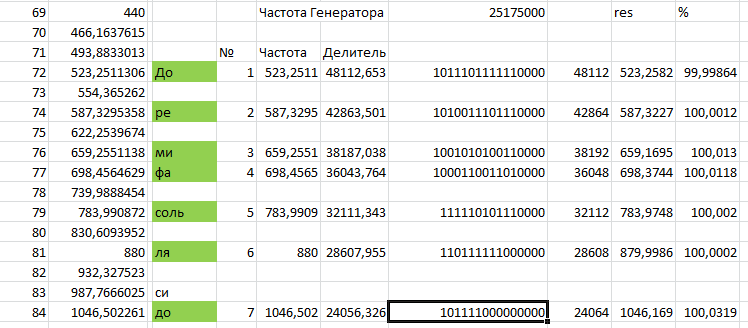
Now that all the calculations are finished, we will describe the logic.

Frequency divider by note number:

 wire [15:0] clkdivider = (note_num == 0) ? 16'd0 : (note_num == 1) ? 16'b1011101111110000 : (note_num == 2) ? 16'b1010011101110000 : (note_num == 3) ? 16'b1001010100110000 : (note_num == 4) ? 16'b1000110011010000 : (note_num == 5) ? 16'b0111110101110000 : (note_num == 6) ? 16'b0110111111000000 : (note_num == 7) ? 16'b0101111000000000 : 16'd0; 

Judging by the picture, the sequencer we get at 64 steps. To do this, increase the bit counter tone.

 reg [27:0] tone; initial tone <= 28'd0; always @(posedge clk) tone <= tone + 1'b1; wire [5:0] step_num = tone[26:(26-5)]; // 6    0  63 

Convert from step number to sequencer to note number:

 wire [2:0] note_num = (step_num == 0) ? 5 : // 1 (step_num == 1) ? 5 : // 2 (step_num == 2) ? 0 : // 3 (step_num == 3) ? 0 : // 4 (step_num == 4) ? 3 : // 5 (step_num == 5) ? 0 : // 6 (step_num == 6) ? 3 : // 7 (step_num == 7) ? 0 : // 8 (step_num == 8) ? 5 : // 9 (step_num == 9) ? 5 : // 10 (step_num ==10) ? 0 : // 11 (step_num ==11) ? 0 : // 12 (step_num ==12) ? 3 : // 13 (step_num ==13) ? 0 : // 14 (step_num ==14) ? 3 : // 15 (step_num ==15) ? 0 : // 16 ...  . . 

 module epm7064_test(clk, audio); input wire clk; output audio; reg [15:0] counter; initial counter <= 16'd0; reg [27:0] tone; initial tone <= 28'd0; always @(posedge clk) tone <= tone + 1'b1; wire [5:0] step_num = tone[26:(26-5)]; wire [2:0] note_num = (step_num == 0) ? 5 : // 1 (step_num == 1) ? 5 : // 2 (step_num == 2) ? 0 : // 3 (step_num == 3) ? 0 : // 4 (step_num == 4) ? 3 : // 5 (step_num == 5) ? 0 : // 6 (step_num == 6) ? 3 : // 7 (step_num == 7) ? 0 : // 8 (step_num == 8) ? 5 : // 9 (step_num == 9) ? 5 : // 10 (step_num ==10) ? 0 : // 11 (step_num ==11) ? 0 : // 12 (step_num ==12) ? 3 : // 13 (step_num ==13) ? 0 : // 14 (step_num ==14) ? 3 : // 15 (step_num ==15) ? 0 : // 16 (step_num ==16) ? 5 : // 17 (step_num ==17) ? 0 : // 18 (step_num ==18) ? 4 : // 19 (step_num ==19) ? 0 : // 20 (step_num ==20) ? 3 : // 21 (step_num ==21) ? 0 : // 22 (step_num ==22) ? 2 : // 23 (step_num ==23) ? 0 : // 24 (step_num ==24) ? 1 : // 25 (step_num ==25) ? 1 : // 26 (step_num ==26) ? 1 : // 27 (step_num ==27) ? 1 : // 28 (step_num ==28) ? 0 : // 29 (step_num ==29) ? 0 : // 30 (step_num ==30) ? 0 : // 31 (step_num ==31) ? 0 : // 32 (step_num ==32) ? 6 : // 33 (step_num ==33) ? 6 : // 34 (step_num ==34) ? 0 : // 35 (step_num ==35) ? 0 : // 36 (step_num ==36) ? 7 : // 37 (step_num ==37) ? 0 : // 38 (step_num ==38) ? 6 : // 39 (step_num ==39) ? 0 : // 40 (step_num ==40) ? 5 : // 41 (step_num ==41) ? 5 : // 42 (step_num ==42) ? 0 : // 43 (step_num ==43) ? 0 : // 44 (step_num ==44) ? 3 : // 45 (step_num ==45) ? 0 : // 46 (step_num ==46) ? 3 : // 47 (step_num ==47) ? 0 : // 48 (step_num ==48) ? 5 : // 49 (step_num ==49) ? 0 : // 50 (step_num ==50) ? 4 : // 51 (step_num ==51) ? 0 : // 52 (step_num ==52) ? 3 : // 53 (step_num ==53) ? 0 : // 54 (step_num ==54) ? 2 : // 55 (step_num ==55) ? 0 : // 56 (step_num ==56) ? 1 : // 57 (step_num ==57) ? 1 : // 58 (step_num ==58) ? 1 : // 59 (step_num ==59) ? 1 : // 60 (step_num ==60) ? 0 : // 61 (step_num ==61) ? 0 : // 62 (step_num ==62) ? 0 : // 63 (step_num ==63) ? 0 : // 64 0; wire [15:0] clkdivider = (note_num == 0) ? 16'd0 : (note_num == 1) ? 16'b1011101111110000 : (note_num == 2) ? 16'b1010011101110000 : (note_num == 3) ? 16'b1001010100110000 : (note_num == 4) ? 16'b1000110011010000 : (note_num == 5) ? 16'b0111110101110000 : (note_num == 6) ? 16'b0110111111000000 : (note_num == 7) ? 16'b0101111000000000 : 16'd0; always @(posedge clk) begin if(counter==0) begin counter <= clkdivider; end else begin counter <= counter - 1'b1; end end reg audio; always @(posedge clk) if(counter==0) audio <= ~audio; endmodule 

Let's start the control auditions.

I think Masha approves;) ^ _ ^

findings

As it turned out, the FPGA with 64 cells is able to act as a sound signal generator for the alarm siren. A project with a melody about a little Christmas tree, took 61 cells from the 64th. And this means that there are still resources, they can be used and created, for example, a musical doorbell (hello 90s!).

Source codes: https://github.com/UA3MQJ/epm7064_audio

When writing the article, the ideas and source codes of the article from the fpga2fun website - Music Box were used .