Information Security Exam Task
Immediately I will voice the puzzle so that there is no anticipation that some cool new encryption method will be shown here.
It is necessary to prove that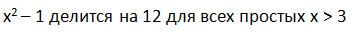
The article is aimed at students, interested citizens and just onlookers. We have information security was the fifth year at the institute. At the lectures on information protection there were many stories about the difficult fate of Russian programmers in the crazy nineties: how they were paid for the work of dumplings, which were made on the ground floor of the enterprise, where they worked, how the moonshine is done, etc. And the remaining time of the lecture was devoted to the actual aspects of information security. The lectures gave a lot of theory on topics that were somehow related to encryption algorithms. At the exam each ticket had a couple of questions on the theory and one problem.
The day before our exam, guys from a parallel group got rid of one problem (described at the beginning of the article), which they could not solve. I sat at work, thought how to solve it, for about an hour. What ideas and first thoughts on the decision were in my head at that moment, I will not say, several years have passed. By the way, I got a problem of the same type on the exam. Below I will show the proof of two typical problems. If you know how to prove differently, post in the comments.
')
So let's get started. The proof is constructed using the Euler theorem .
I repeat the task again. It is necessary to prove that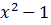 divided by 12 for all simple x> 3.
divided by 12 for all simple x> 3.
x and 12 are mutually simple, then by Euler, divided by 12, i.e. the remainder of the division is 0 (in the theorem, the unit is transferred to the right-hand side of the equality, let's do the same)
divided by 12, i.e. the remainder of the division is 0 (in the theorem, the unit is transferred to the right-hand side of the equality, let's do the same)
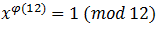
For the number 12, there are four smaller ones and numbers that are mutually simple with it (1, 5, 7, 11), so the Euler function takes on four values:
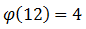

Move the unit from the right side of the equality to the left and use the formula from the school, factoring the difference of squares:
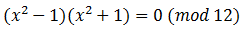
We shorten by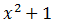 :
:
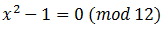
Q.E.D.
And now here is another typical problem that I came across in the exam. When the decision was shown to the teacher, for some reason he was surprised, because, as he later said, it would be enough to simply count in the forehead, raise to a power and show that one number is divided by another. And he sees the decision that I showed him for the first time. You always think that you need to apply theorems, corollaries, axioms for the proof, but it turns out that “you could just count it on the forehead”.
Prove that number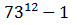 divided by 105.
divided by 105.
If the number is divided completely, then the remainder is 0. The numbers 73 and 105 are mutually simple => by the t. Euler:

We calculate the Euler function. Since we’ll go through all the numbers less than 105 and search for mutually simple ones with 105 for a long time, we will factor 105 into factors and find the Euler function for each of them, and then simply multiply:
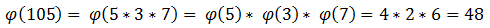
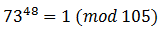
Move the unit to the left and factor it out:
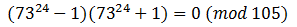
We shorten by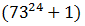 :
:
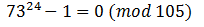
Factor and shorten again:
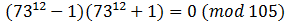
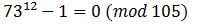
Remainder of the division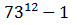 by 105 - zero, division is complete. PM
by 105 - zero, division is complete. PM
Perhaps, this decision will be useful to someone, but I hope that you will have something more interesting on your ZI.
It is necessary to prove that
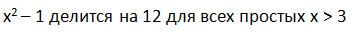
The article is aimed at students, interested citizens and just onlookers. We have information security was the fifth year at the institute. At the lectures on information protection there were many stories about the difficult fate of Russian programmers in the crazy nineties: how they were paid for the work of dumplings, which were made on the ground floor of the enterprise, where they worked, how the moonshine is done, etc. And the remaining time of the lecture was devoted to the actual aspects of information security. The lectures gave a lot of theory on topics that were somehow related to encryption algorithms. At the exam each ticket had a couple of questions on the theory and one problem.
The day before our exam, guys from a parallel group got rid of one problem (described at the beginning of the article), which they could not solve. I sat at work, thought how to solve it, for about an hour. What ideas and first thoughts on the decision were in my head at that moment, I will not say, several years have passed. By the way, I got a problem of the same type on the exam. Below I will show the proof of two typical problems. If you know how to prove differently, post in the comments.
')
So let's get started. The proof is constructed using the Euler theorem .
I repeat the task again. It is necessary to prove that
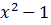 divided by 12 for all simple x> 3.
divided by 12 for all simple x> 3.x and 12 are mutually simple, then by Euler,
 divided by 12, i.e. the remainder of the division is 0 (in the theorem, the unit is transferred to the right-hand side of the equality, let's do the same)
divided by 12, i.e. the remainder of the division is 0 (in the theorem, the unit is transferred to the right-hand side of the equality, let's do the same)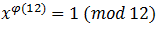
For the number 12, there are four smaller ones and numbers that are mutually simple with it (1, 5, 7, 11), so the Euler function takes on four values:
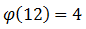

Move the unit from the right side of the equality to the left and use the formula from the school, factoring the difference of squares:
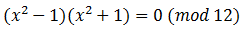
We shorten by
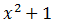 :
: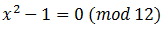
Q.E.D.
And now here is another typical problem that I came across in the exam. When the decision was shown to the teacher, for some reason he was surprised, because, as he later said, it would be enough to simply count in the forehead, raise to a power and show that one number is divided by another. And he sees the decision that I showed him for the first time. You always think that you need to apply theorems, corollaries, axioms for the proof, but it turns out that “you could just count it on the forehead”.
Prove that number
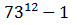 divided by 105.
divided by 105.If the number is divided completely, then the remainder is 0. The numbers 73 and 105 are mutually simple => by the t. Euler:

We calculate the Euler function. Since we’ll go through all the numbers less than 105 and search for mutually simple ones with 105 for a long time, we will factor 105 into factors and find the Euler function for each of them, and then simply multiply:
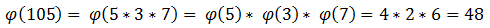
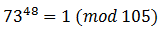
Move the unit to the left and factor it out:
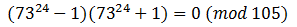
We shorten by
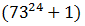 :
: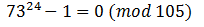
Factor and shorten again:
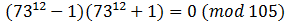
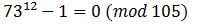
Remainder of the division
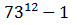 by 105 - zero, division is complete. PM
by 105 - zero, division is complete. PMPerhaps, this decision will be useful to someone, but I hope that you will have something more interesting on your ZI.
Source: https://habr.com/ru/post/317818/
All Articles