Recursion formulas for calculating iterative summation errors of binary numbers of limited length
In this article we will continue the consideration of the problem of computer calculations of decimal numbers with the help of binary arithmetic, which was addressed in the previous topic [1]. The article discusses errors that are commonly referred to in literature as rounding errors. And, in particular, errors that are generated as a result of the iterative summation of a large number of identical decimal numbers, represented in binary form by a limited bit space. As a result of the research, simple recurrence relations were obtained, which allow to accurately determine the error of computer iterative calculations of the partial sums of any number of identical terms, at any iteration step.
We will consider real positive binary numbers with a fixed number of L significant digits. By a fixed number L of significant digits, we mean L digits, which are counted from left to right, starting from the highest nonzero digit. The missing number of digits in the number to the right is padded with zeros. So, if the number of significant digits is fixed with the value L = 5, then the number 0.0011 will have the following significant digits: 11000. If we now write our number to a 5-bit computer as a floating-point number, then the machine mantissa will be written: .11000 . This number will be represented in the computer in a normalized form with an exponent equal to 2 ^ -2.
A floating-point number is written in a machine word, as the product of a fractional mantissa by an exponent, the order of which indicates the position of a point in a number represented in its natural form. If the number of digits of the mantissa number does not coincide with the number of L bits of the machine mantissa, the number is normalized by shifting the mantissa to one side or the other so that the highest nonzero digit of the number is located in the highest digit of the machine mantissa. The order of the exponent is adjusted for the number of shifts.
Consider the number in a natural form. If the number of its significant digits exceeds some fixed number of L digits, then it must be converted so that the number of its significant digits becomes equal to L. This is achieved by discarding the extra low-order digits. When discarding low-order digits, the number may be rounded to L digits, or extra low-order digits are simply truncated. So, in the case of truncation, the binary number 10.0011, presented in its natural form, for L = 5, will be written as 10.001. The same number, written in an exponential normalized form, will look like 0.10001 * 2 ^ 2. Here we have two equivalent entries of the same number.
')
Reduction of the number presented in its natural form to a number with the number of significant digits L will be called optimization. We introduce this concept to distinguish it from the operation of normalizing numbers written in an exponential form. From a mathematical point of view, these are two equivalent operations.
Next, we will consider the case of truncating the lower digits in the binary number without rounding. The numbers will be considered presented in the natural form.
Suppose we have a number 2 ^ p ≤Z <2 ^ (p + 1), where p is a signed integer equal to the distance from the separating point to the highest nonzero digit in the number Z, written in its natural form. If the highest nonzero digit is located to the left of the point, then p> 0. If the digit is located to the right of the point, then p <0. So, for the number Z = 0.000101 we will have p = -4 and for this case: 2 ^ (- 4) ≤Z <2 ^ (- 3).
Consider the sequence of real binary numbers X 0 , X 1 , ... X i ... lying in the intervals:
2 ^ p ≤ X 0 <2 ^ (1 + p) ≤ X 1 <2 ^ (2 + p); ...; 2 ^ (i + p) ≤ X i <2 ^ (i + p + 1) ...
For example, for p = -3 we will have 2 ^ p = 2 ^ -3 = 0.001. Our sequence will then look like 0.001 ≤ X 0 <0.01 ≤ X 1 <0.1, ..., 2 ^ (i -3) ≤ X i <2 ^ (i -2) ...
Take some real number 2 ^ (i + p) ≤ X i <2 ^ (i + p + 1) with a limited number of L significant digits. Next, take the sum of the k i elementary terms: Z + Z + ... = k i Z, where Z = X 0 , k i ≥ 0 is an integer. Choose k i such that 2 ^ (i + p) ≤ X i + k i Z <2 ^ (i + p +1). In this sum, the maximum number of k i elementary terms of Z, at which the value of the sum does not exceed the right boundary of the interval, can be found by the formula k i = ⌊ (2 ^ (i + p + 1) -X i ) / Z⌋, where brackets ⌋ means round down to the nearest integer.
If we now add another elementary term Z to X i + k i Z, we get X i + 1 = X i + k i Z + Z = X i + Z (k i +1) ≥ 2 ^ (i + p +1 ). The value of the newly received amount will exceed or will be equal to the right boundary value of the interval. Therefore, the number of digits in the number X i + 1 = X i + Z (k i +1) becomes L + 1. To fulfill the requirement that the number of significant digits be equal to L, the resulting number must be optimized, i.e. lead to the number in which there will be L significant digits. To do this, it is necessary to discard the younger digit. The operation of discarding the lower digit in the number X i will be written as X i ¬1 . For example, if in the number X = 10.0011 one small digit is discarded, then it will be written as X ¬1 = 10.001 . In the general case, the entry X ¬t will mean that among the X the t low-order bits are dropped.
After at a certain iterative step the partial sum X i + 1 = X i + Z (k i +1) exceeds the value 2 ^ (i + p +1), which we will call the right boundary value, the highest nonzero digit of the sum will be offset from a fixed point to the left. The total number of significant digits will exceed the L number by one and the result should be optimized. Since at the i-th iteration step as a result of the optimization, in the number X i the lower digit is discarded, the number becomes equal to X i ¬1 , then the younger digit in the term Z can also be discarded, since it will not affect further calculations.
For example. Let L = 5. Find the sum of two numbers X = 1.10111 and Z = 0.10011. Since the number of digits in X exceeds the value of L, it must be optimized. After optimization we get: X ¬1 = 1.1011. Add to this number Z = 0.1001 ** 1 **. We get X ¬1 + Z = 1.1011 + 0.1001 ** 1 ** = 10.0100 ** 1 **. Here the number of digits after the decimal point in the term X ¬1 is less than the number of digits in the term Z. Therefore, the lower digit in Z, marked in bold, on the one hand, always adds up to zero, and on the other hand, the result of adding lower digits in this case is out of range L significant digits and, therefore, when truncated, does not affect the total amount. It follows that the amount will not change if it is written as X ¬1 + Z ¬1 = 1.1011 + 0.1001 = 10.0100. Since in this sum the number of digits exceeded the value of L, the resulting number should also be optimized. Rejecting the lower digit, we get an optimized number of 10.010 with L = 5 significant digits.
Thus, the values of the partial sums X i and X i + 1 differ by a maximum of k i elementary terms. The number of significant digits of partial sums lying in the interval [X i , X i + 1 ) is L and therefore their values are calculated without rounding and, accordingly, do not introduce errors. The addition of the (k i + 1 ) -th term to the partial sum leads to the excess of the right boundary value or its equality. If the partial sum at any iteration step exceeds or equals the right limit value, then the number of significant digits in the sum becomes equal to L + 1 and optimization is required. After each excess of the right boundary value, the number of significant digits of elementary terms Z, participating in the formation of new partial sums, decreases by one and after the ith right boundary value, the elementary term becomes equal to Z ¬i .
X i + 1 = (X i + (k i + 1 +1) Z ¬i ) ¬1 , X 0 = Z, i = 0.1 ...
k i + 1 = ⌊ (2 ^ (p + i) -X i ) / Z ¬i , p is a signed integer.
The iteration step number N i + 1 , at which the partial sum X i + 1 exceeded the right boundary value, can be determined by the recurrence relation:
N i + 1 = (k i + 1 +1) + N i .
Let us now consider what error we get in iterative summation of decimal real numbers, represented in binary form, as a result of the truncation operation.
It is known that any decimal number X represented in binary form, after truncating the number of significant digits, can be written as X = B + g, where B is the representation of the decimal number X in binary form with a limited fixed number of significant digits, g is the absolute error representation of the number as a result of truncation. This error can be defined as g = XB, g ≥0. When summing i elementary terms, this error accumulates and becomes equal to ig.
However, this is not the only error that is formed by the recurrent addition of the same elementary terms. As a result of rounding or truncation, when recurrently calculating partial sums, rounding errors are also generated.
The recurrence relations that we derived make it possible at any iteration step to obtain exact error values for calculating the sum of elementary terms that have the same values.
Consider, for example, partial sums of elementary terms Z = 0.0011101, for which L = 5. For the number Z, we will have p = 0.001. Table 1 shows the results of the addition of 10 elementary terms for each iteration step.
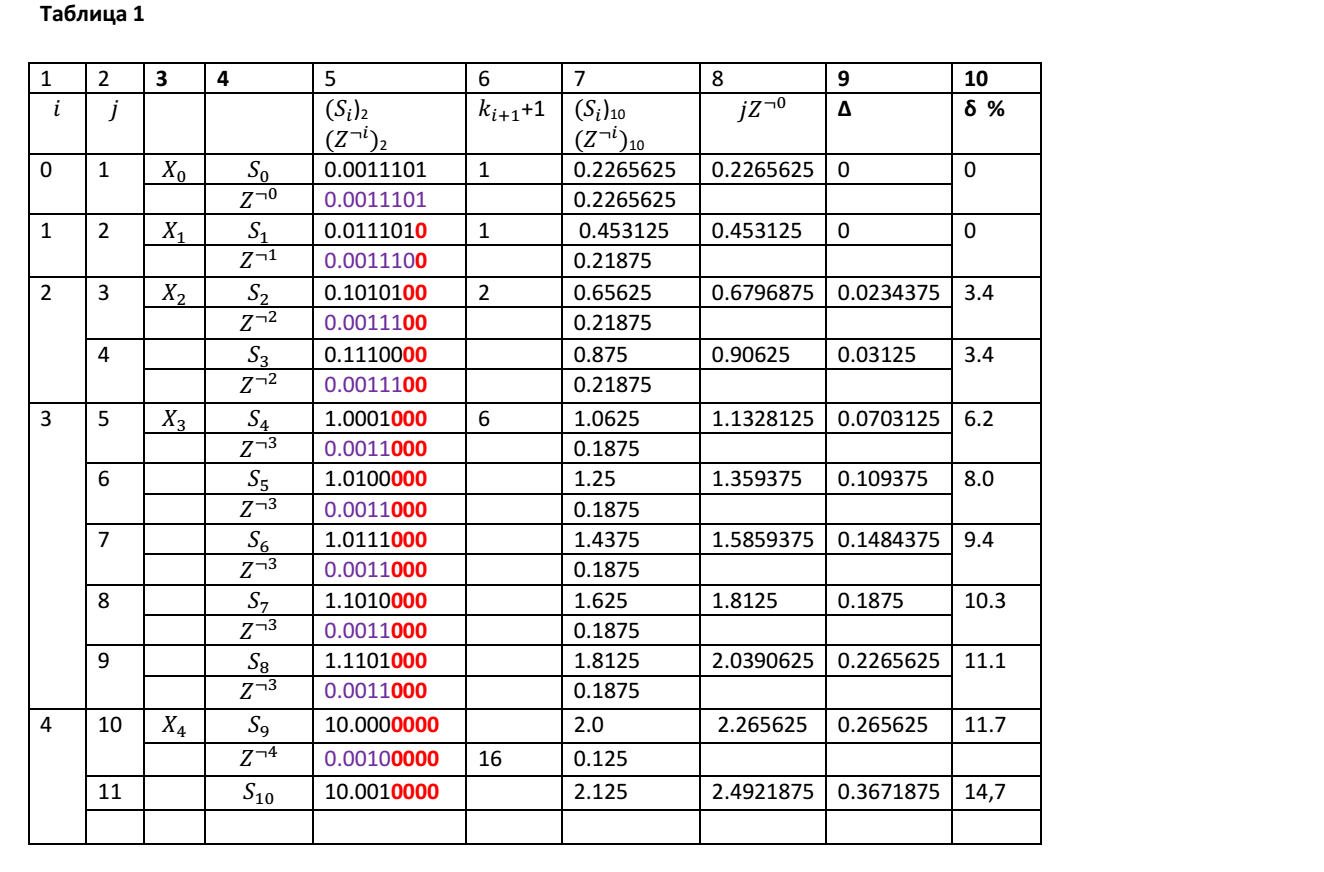
Column 1 of the table shows the numbers i of the partial sums X i that exceeded or became equal to the right edge of the interval. The second column shows the numbers of iterations j. Column 3 shows the designations of the partial sums X i for a certain value of i. Column 4 of the table shows each other under each other, respectively, the designations of the partial sums S j and the elementary terms Z ¬i for each iteration step. Column 5 shows each other, respectively, the values of the partial sums S j and the elementary terms Z ¬i for each iteration step. The red font marked digits of numbers that do not participate in the formation of partial sums. Column 6 shows the values of the coefficients k i + 1 +1, which are used in our recurrent formula to calculate X i + 1 . Column 7 shows each other under each other, respectively, the values of the partial sums S j and the elementary terms Z ¬i for each iteration step in decimal form. Column 8 shows the theoretical values of the sum of the elementary components of Z, provided that rounding errors are not taken into account. Column 9 presents the values of the absolute calculation errors at each iteration step, which are calculated by the formula Δ = (S j ) 10 - jZ ¬0 . Column 9 presents the values of relative errors calculated by the formula: δ = Δ / jZ ¬0 .
As can be seen from the table above, even under the condition that the elementary terms are presented accurately, without representation errors, in the process of iterative summation such an error is very quickly formed that calculations at a certain iteration step become meaningless. The reason for this error lies in the limited machine words, as well as in the normalization procedure, or, in our case, the optimization of the representation of numbers.
Below we present Table 2, in which the values of partial sums are presented during iterative summation of the decimal number 0.1 in binary form with a fixed number of significant digits for the 51 bit mantissa. The table shows the values of the partial sums at the points of exceeding the right boundary values. The numbers in bold in the table are binary. Non-bold numbers are numbers represented in decimal code. This table shows the values of the partial sums X i , the values of the coefficients k i + 1 +1 for finding the next partial sum X i + 1 in accordance with our recurrence relations.
The iteration step number N i + 1 , at which the next partial amount exceeded the right limit value, can be determined by the recurrence relation: N i + 1 = (k i + 1 +1) + N i .
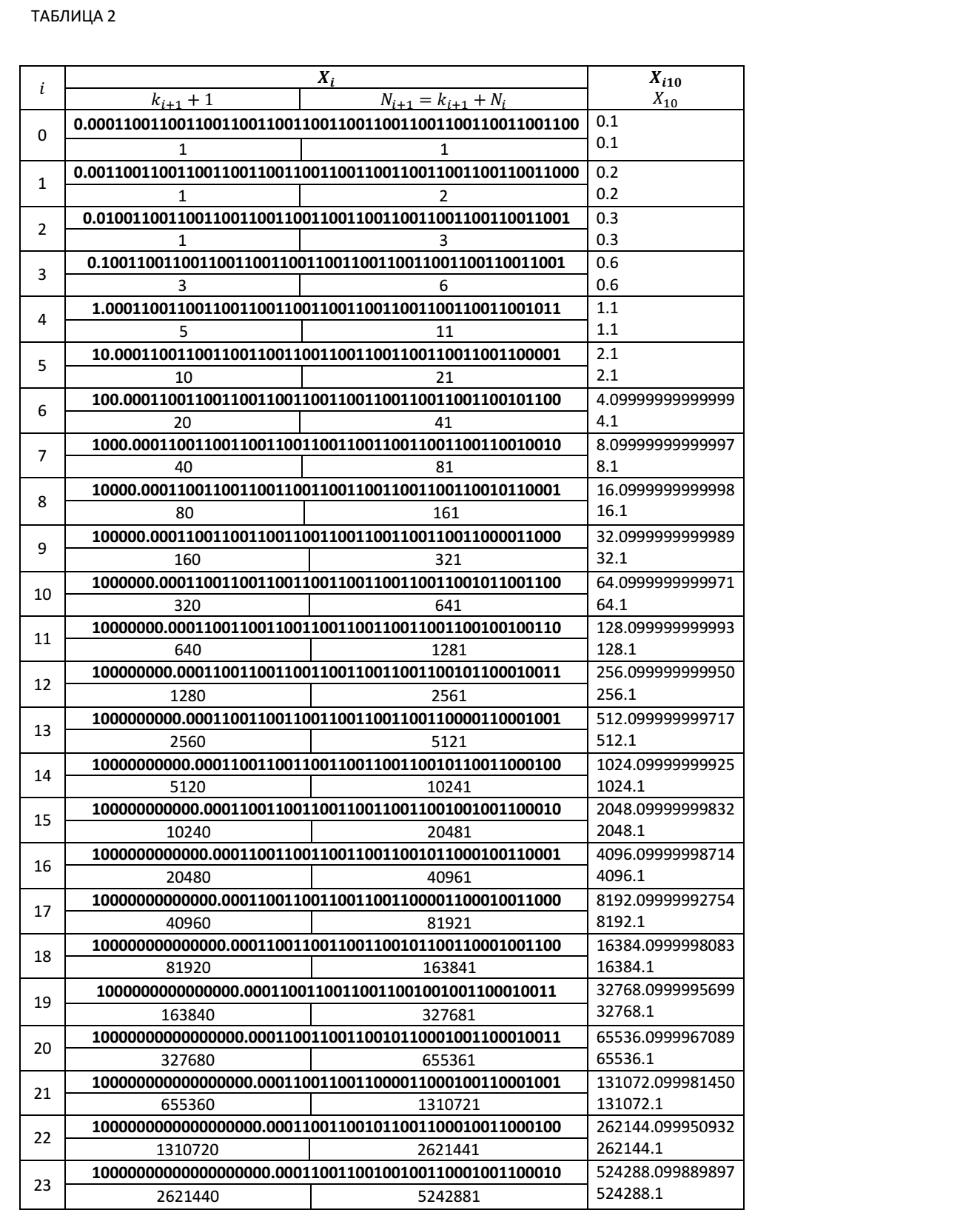
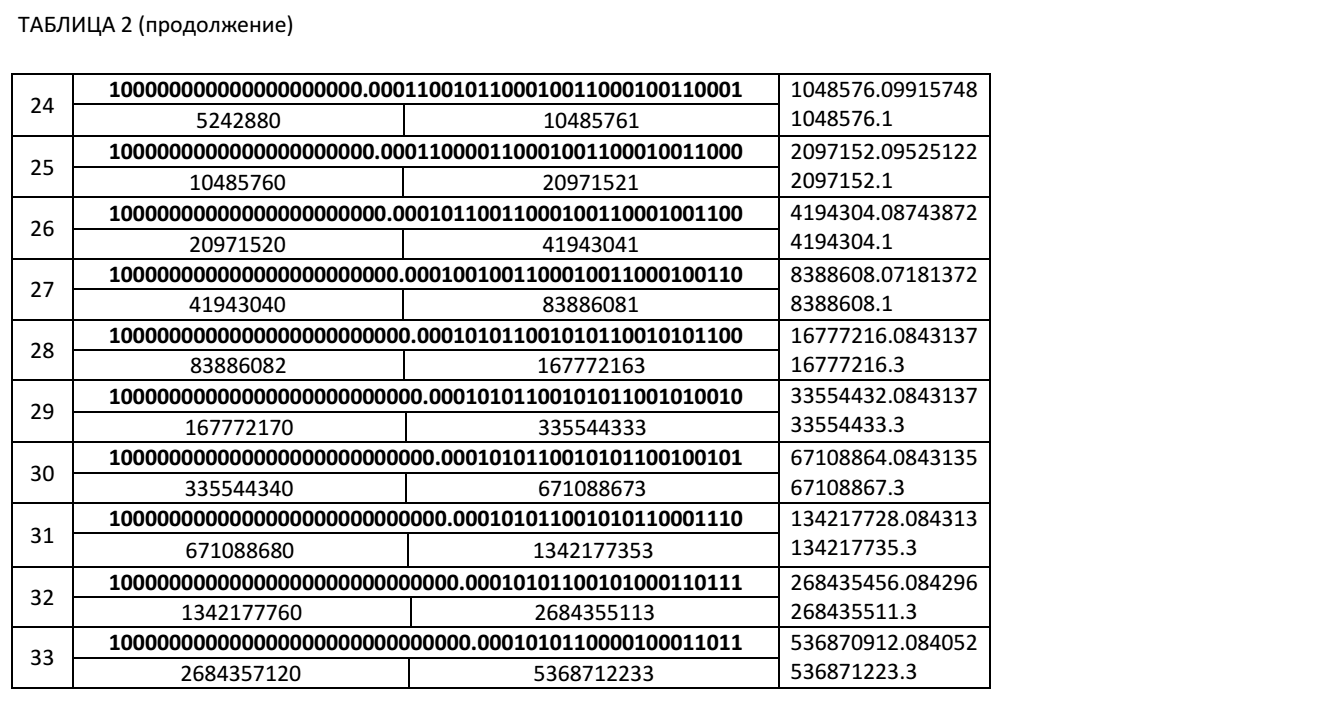
As can be seen from Table 2, with the number of iterations 5368712233 already in the 6th sign of the partial sum we have the wrong number. The absolute computation error for this case is Δ = 536871223.3-536870912.084052 = 311.215948. And the relative error will be equal to δ = 311.215948 / 536871223.3≈0.0000006 = 0.00006%.
At the same time, if we calculate the error in representing the decimal number 0.1 in binary form with 51 significant digits, then we will have: 0.1 = 0.0001100110011001100110011001100110011001100110011001100≈ 0.09999999999999997779
Δ = 0.1-0.09999999999999997779≈2.221 * 10 ^ (- 17),
δ = 2.221 * 10 ^ (- 17) /0.1=2.221*10 ^ (- 16) = 14 * 10 ^ (- 14)%.
At the iteration step, equal to 5368712233, the total absolute error of the representation takes the value 5368712233 * 14 * 10 ^ (- 18) ≈ 0.000000075. The relative error of representation does not change at any iteration step.
As we can see, the absolute error of representation is negligible compared to the rounding error in iterative summation.
The recurrent formulas we presented here allowed us to obtain accurate calculated rounding errors in the iterative summation of a large number of identical decimal terms represented in binary code.
The author thanks the user mayorovp for the inaccuracies found.
LITERATURE
1. habrahabr.ru/post/309812
We will consider real positive binary numbers with a fixed number of L significant digits. By a fixed number L of significant digits, we mean L digits, which are counted from left to right, starting from the highest nonzero digit. The missing number of digits in the number to the right is padded with zeros. So, if the number of significant digits is fixed with the value L = 5, then the number 0.0011 will have the following significant digits: 11000. If we now write our number to a 5-bit computer as a floating-point number, then the machine mantissa will be written: .11000 . This number will be represented in the computer in a normalized form with an exponent equal to 2 ^ -2.
A floating-point number is written in a machine word, as the product of a fractional mantissa by an exponent, the order of which indicates the position of a point in a number represented in its natural form. If the number of digits of the mantissa number does not coincide with the number of L bits of the machine mantissa, the number is normalized by shifting the mantissa to one side or the other so that the highest nonzero digit of the number is located in the highest digit of the machine mantissa. The order of the exponent is adjusted for the number of shifts.
Consider the number in a natural form. If the number of its significant digits exceeds some fixed number of L digits, then it must be converted so that the number of its significant digits becomes equal to L. This is achieved by discarding the extra low-order digits. When discarding low-order digits, the number may be rounded to L digits, or extra low-order digits are simply truncated. So, in the case of truncation, the binary number 10.0011, presented in its natural form, for L = 5, will be written as 10.001. The same number, written in an exponential normalized form, will look like 0.10001 * 2 ^ 2. Here we have two equivalent entries of the same number.
')
Reduction of the number presented in its natural form to a number with the number of significant digits L will be called optimization. We introduce this concept to distinguish it from the operation of normalizing numbers written in an exponential form. From a mathematical point of view, these are two equivalent operations.
Next, we will consider the case of truncating the lower digits in the binary number without rounding. The numbers will be considered presented in the natural form.
Suppose we have a number 2 ^ p ≤Z <2 ^ (p + 1), where p is a signed integer equal to the distance from the separating point to the highest nonzero digit in the number Z, written in its natural form. If the highest nonzero digit is located to the left of the point, then p> 0. If the digit is located to the right of the point, then p <0. So, for the number Z = 0.000101 we will have p = -4 and for this case: 2 ^ (- 4) ≤Z <2 ^ (- 3).
Consider the sequence of real binary numbers X 0 , X 1 , ... X i ... lying in the intervals:
2 ^ p ≤ X 0 <2 ^ (1 + p) ≤ X 1 <2 ^ (2 + p); ...; 2 ^ (i + p) ≤ X i <2 ^ (i + p + 1) ...
For example, for p = -3 we will have 2 ^ p = 2 ^ -3 = 0.001. Our sequence will then look like 0.001 ≤ X 0 <0.01 ≤ X 1 <0.1, ..., 2 ^ (i -3) ≤ X i <2 ^ (i -2) ...
Take some real number 2 ^ (i + p) ≤ X i <2 ^ (i + p + 1) with a limited number of L significant digits. Next, take the sum of the k i elementary terms: Z + Z + ... = k i Z, where Z = X 0 , k i ≥ 0 is an integer. Choose k i such that 2 ^ (i + p) ≤ X i + k i Z <2 ^ (i + p +1). In this sum, the maximum number of k i elementary terms of Z, at which the value of the sum does not exceed the right boundary of the interval, can be found by the formula k i = ⌊ (2 ^ (i + p + 1) -X i ) / Z⌋, where brackets ⌋ means round down to the nearest integer.
If we now add another elementary term Z to X i + k i Z, we get X i + 1 = X i + k i Z + Z = X i + Z (k i +1) ≥ 2 ^ (i + p +1 ). The value of the newly received amount will exceed or will be equal to the right boundary value of the interval. Therefore, the number of digits in the number X i + 1 = X i + Z (k i +1) becomes L + 1. To fulfill the requirement that the number of significant digits be equal to L, the resulting number must be optimized, i.e. lead to the number in which there will be L significant digits. To do this, it is necessary to discard the younger digit. The operation of discarding the lower digit in the number X i will be written as X i ¬1 . For example, if in the number X = 10.0011 one small digit is discarded, then it will be written as X ¬1 = 10.001 . In the general case, the entry X ¬t will mean that among the X the t low-order bits are dropped.
After at a certain iterative step the partial sum X i + 1 = X i + Z (k i +1) exceeds the value 2 ^ (i + p +1), which we will call the right boundary value, the highest nonzero digit of the sum will be offset from a fixed point to the left. The total number of significant digits will exceed the L number by one and the result should be optimized. Since at the i-th iteration step as a result of the optimization, in the number X i the lower digit is discarded, the number becomes equal to X i ¬1 , then the younger digit in the term Z can also be discarded, since it will not affect further calculations.
For example. Let L = 5. Find the sum of two numbers X = 1.10111 and Z = 0.10011. Since the number of digits in X exceeds the value of L, it must be optimized. After optimization we get: X ¬1 = 1.1011. Add to this number Z = 0.1001 ** 1 **. We get X ¬1 + Z = 1.1011 + 0.1001 ** 1 ** = 10.0100 ** 1 **. Here the number of digits after the decimal point in the term X ¬1 is less than the number of digits in the term Z. Therefore, the lower digit in Z, marked in bold, on the one hand, always adds up to zero, and on the other hand, the result of adding lower digits in this case is out of range L significant digits and, therefore, when truncated, does not affect the total amount. It follows that the amount will not change if it is written as X ¬1 + Z ¬1 = 1.1011 + 0.1001 = 10.0100. Since in this sum the number of digits exceeded the value of L, the resulting number should also be optimized. Rejecting the lower digit, we get an optimized number of 10.010 with L = 5 significant digits.
Thus, the values of the partial sums X i and X i + 1 differ by a maximum of k i elementary terms. The number of significant digits of partial sums lying in the interval [X i , X i + 1 ) is L and therefore their values are calculated without rounding and, accordingly, do not introduce errors. The addition of the (k i + 1 ) -th term to the partial sum leads to the excess of the right boundary value or its equality. If the partial sum at any iteration step exceeds or equals the right limit value, then the number of significant digits in the sum becomes equal to L + 1 and optimization is required. After each excess of the right boundary value, the number of significant digits of elementary terms Z, participating in the formation of new partial sums, decreases by one and after the ith right boundary value, the elementary term becomes equal to Z ¬i .
X i + 1 = (X i + (k i + 1 +1) Z ¬i ) ¬1 , X 0 = Z, i = 0.1 ...
k i + 1 = ⌊ (2 ^ (p + i) -X i ) / Z ¬i , p is a signed integer.
The iteration step number N i + 1 , at which the partial sum X i + 1 exceeded the right boundary value, can be determined by the recurrence relation:
N i + 1 = (k i + 1 +1) + N i .
Let us now consider what error we get in iterative summation of decimal real numbers, represented in binary form, as a result of the truncation operation.
It is known that any decimal number X represented in binary form, after truncating the number of significant digits, can be written as X = B + g, where B is the representation of the decimal number X in binary form with a limited fixed number of significant digits, g is the absolute error representation of the number as a result of truncation. This error can be defined as g = XB, g ≥0. When summing i elementary terms, this error accumulates and becomes equal to ig.
However, this is not the only error that is formed by the recurrent addition of the same elementary terms. As a result of rounding or truncation, when recurrently calculating partial sums, rounding errors are also generated.
The recurrence relations that we derived make it possible at any iteration step to obtain exact error values for calculating the sum of elementary terms that have the same values.
Consider, for example, partial sums of elementary terms Z = 0.0011101, for which L = 5. For the number Z, we will have p = 0.001. Table 1 shows the results of the addition of 10 elementary terms for each iteration step.

Column 1 of the table shows the numbers i of the partial sums X i that exceeded or became equal to the right edge of the interval. The second column shows the numbers of iterations j. Column 3 shows the designations of the partial sums X i for a certain value of i. Column 4 of the table shows each other under each other, respectively, the designations of the partial sums S j and the elementary terms Z ¬i for each iteration step. Column 5 shows each other, respectively, the values of the partial sums S j and the elementary terms Z ¬i for each iteration step. The red font marked digits of numbers that do not participate in the formation of partial sums. Column 6 shows the values of the coefficients k i + 1 +1, which are used in our recurrent formula to calculate X i + 1 . Column 7 shows each other under each other, respectively, the values of the partial sums S j and the elementary terms Z ¬i for each iteration step in decimal form. Column 8 shows the theoretical values of the sum of the elementary components of Z, provided that rounding errors are not taken into account. Column 9 presents the values of the absolute calculation errors at each iteration step, which are calculated by the formula Δ = (S j ) 10 - jZ ¬0 . Column 9 presents the values of relative errors calculated by the formula: δ = Δ / jZ ¬0 .
As can be seen from the table above, even under the condition that the elementary terms are presented accurately, without representation errors, in the process of iterative summation such an error is very quickly formed that calculations at a certain iteration step become meaningless. The reason for this error lies in the limited machine words, as well as in the normalization procedure, or, in our case, the optimization of the representation of numbers.
Below we present Table 2, in which the values of partial sums are presented during iterative summation of the decimal number 0.1 in binary form with a fixed number of significant digits for the 51 bit mantissa. The table shows the values of the partial sums at the points of exceeding the right boundary values. The numbers in bold in the table are binary. Non-bold numbers are numbers represented in decimal code. This table shows the values of the partial sums X i , the values of the coefficients k i + 1 +1 for finding the next partial sum X i + 1 in accordance with our recurrence relations.
The iteration step number N i + 1 , at which the next partial amount exceeded the right limit value, can be determined by the recurrence relation: N i + 1 = (k i + 1 +1) + N i .


As can be seen from Table 2, with the number of iterations 5368712233 already in the 6th sign of the partial sum we have the wrong number. The absolute computation error for this case is Δ = 536871223.3-536870912.084052 = 311.215948. And the relative error will be equal to δ = 311.215948 / 536871223.3≈0.0000006 = 0.00006%.
At the same time, if we calculate the error in representing the decimal number 0.1 in binary form with 51 significant digits, then we will have: 0.1 = 0.0001100110011001100110011001100110011001100110011001100≈ 0.09999999999999997779
Δ = 0.1-0.09999999999999997779≈2.221 * 10 ^ (- 17),
δ = 2.221 * 10 ^ (- 17) /0.1=2.221*10 ^ (- 16) = 14 * 10 ^ (- 14)%.
At the iteration step, equal to 5368712233, the total absolute error of the representation takes the value 5368712233 * 14 * 10 ^ (- 18) ≈ 0.000000075. The relative error of representation does not change at any iteration step.
As we can see, the absolute error of representation is negligible compared to the rounding error in iterative summation.
The recurrent formulas we presented here allowed us to obtain accurate calculated rounding errors in the iterative summation of a large number of identical decimal terms represented in binary code.
The author thanks the user mayorovp for the inaccuracies found.
LITERATURE
1. habrahabr.ru/post/309812
Source: https://habr.com/ru/post/317786/
All Articles