Giant component: hooks for fishing, galaxy clusters, molecular biotechnology, nanomaterials
Being engaged in Knut translations, I came across a mention of a very interesting feature of our universe. The birth of a giant component . Everyone met with this phenomenon. For example, I remember the boxes with fishing hooks. When the hooks were 5-15 everything is fine, but there is a certain critical mass, after which a single lump was obtained. Intuitively, I feel that this is a very important phenomenon, which manifests itself in many disciplines, from information theory to molecular chemistry and biotechnology. I bring to your attention a translation of an easy and visual article on this topic. The word Brian Hayes.

An unnecessary product of my document scanning project is a bunch of extracted clips.
')
The other day I made a discovery: if you grab one of the discarded staples and lift it, a whole ball of tangled twisted metal will rise after it, leaving only a couple of staples at the bottom of the bowl. When I noticed this, I first thought, “Hm, this is funny.” Then "Oh, of course: Erdős-Rényi." And the third thought ... well, I'm still working on it, and also on the fourth, fifth and sixth.

Erdős and Rényi are Paul Erdős and Alfréd Rényi, who wrote a great work on the “Evolution of Random Graphs” 50 years ago (Publications of the Mathematical Institute of the Hungarian Academy of Sciences, 1960, 5: 17–61). Their article was not quite the debut appearance of random graphs in mathematical literature, but is considered the original origin of the theory.
In one version of the Erdős-Rényi process, you start with a set of isolated vertices n and then add random edges one by one; In particular, at each stage, you select any two vertices from among all the pairs that are no longer connected, and then draw an edge between them.
It turns out that a dramatic change in the nature of graphs occurs when the number of faces reaches n / 2. Below this threshold, a graph consists of many small, isolated components; above n / 2, the fragments merge into one giant component, which includes almost all the vertices.
“The birth of the giant component” was later described in more detail in an even larger article - it covered the entire question of random structures and algorithms (1993, 4: 233-358) and was written by Swante Janson, Donald Knuth, Tomasz Lutsaka and Boris Pittel.
What made me think about the connection between the Erdős-Rényi graphs and the clew? In my mind there was something like a long, straight, middle part of the bracket corresponds to the edge of the graph, and the curved parts that can interlock with each other are the vertices. Thus, one bracket is a graph consisting of two vertices connected along one edge. When two brackets are connected, their two vertices merge, and a connected graph of three vertices and two edges remains. Since each bracket gives one edge and at most two vertices to a graph, the number of edges must be at least half the number of vertices. Thus, the graph always exceeds the threshold when a giant component is formed, according to Erdős and Rényi.
With the computational part of this analysis, everything seems clear, but I am afraid that the rest is not so easy to understand. Regardless of what happens in the staple ball, the evolution of the system is not well modeled by the Erdős-Rényi process, which adds faces to a fixed set of vertices. Instead, each bracket gives 2 faces and 2 vertices.
The tipping point that makes a bundle of staples stick together is the merging of vertices when braces are held together; There is no such merger in the Erdős-Rényi process. The main problem here is that the Erdős-Rényi graphs are purely topological - there is no concept of distance, and any two vertices can have an edge connecting them. But the bracket graph has important geometric constraints. Two vertices can be connected by an edge only if the distance between them is approximately equal to the length of the bracket.
The geometric structure involves attempts to build various types of models - perhaps, that describes the molecular structure of liquids and solids. Water molecules, for example, are linked to each other by a network of hydrogen bonds; each hydrogen atom in one molecule can have a bond with the oxygen atom of another molecule. But connections cannot extend to arbitrary distances; they spread only between neighboring molecules. As a result, a three-dimensional structure was obtained, the main motive of which is a tetrahedron with an oxygen atom in the center and hydrogen atoms in the four corners. (There is also a diagram of a two-dimensional model, known as ice area). We can imagine how something like this happens with brackets, where two bent ends can form hydrogen bonds as a bond with other nearby braces.
But with such chemical elements there is also a problem. The atoms have a fixed valence (more or less - let's not find fault); in water, for example, each hydrogen atom can form a hydrogen bond with only one oxygen atom. But we have no reason to believe that the hooked ends of the staples can hook only one edge of the other bracket. In fact, if such a restriction existed, then the brackets could form only chains and rings, not dense clusters. On close examination of a cluster of brackets, it is easy to find places where three or more brackets are linked together at the same point. Carefully peering deep into the staple clusters, I found a staple, to which at least six other clips were clinging.
Another physical process that could provide a model for the main graph is aggregation of limited distribution. This is the mechanism responsible for the filigree pattern.
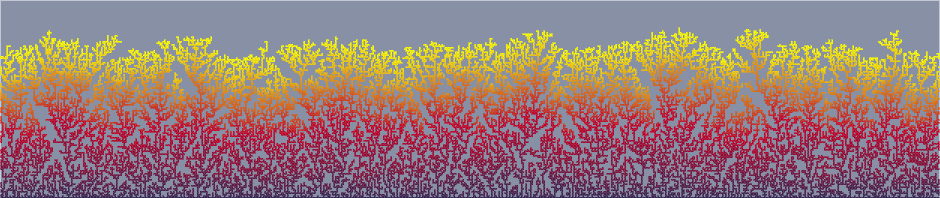
It is produced by sticky particles that drift randomly until they stumble onto the ground or touch another particle that is already in contact (directly or indirectly) with the base.
Another factor to consider is the fact that spatial dimensions are undoubtedly important here. On the one hand, it just gives more opportunities to maneuver in three dimensions, more opportunities to cling to a neighbor. But specifically in the case of staples, there is another reason: being chained to a plane, it is difficult for them to connect.

Scattered on a flat board, they refuse to fold, even when spinning vigorously. The reason, apparently, is that safe joints are formed only when the brackets can turn 90 degrees and mate. In this regard, it is important that brackets are used, quite diverse in shape, with hooked ends bent about 180 degrees during the binding process and which basically retained an angle of more than 90 degrees after they were pulled out of the paper.
I wondered how the shiny new braces would behave and I conducted an experiment (Materials and methods: 630 Stanley Bostitch chisel-point staples, model SBS191 / 4CP, freshly dispensed from an open-jaw Swingline stapler.)
I was, to put it mildly, surprised by the result. Although the stack of staples was somewhat looser and more subtle, the gist really wasn't that different. Again we witness the birth of a giant component.
Barry Cipra : It might be worthwhile to repeat the experiment with new braces, pausing every time you add braces (say every 10 or 20 brackets), shaking what is already in the bowl, and then watch how a large congestion forms when you take one of the brackets. Perhaps it would be nice to repeat the shake and pause between adding staples several times and watch the statistics. I assume that the (average) percentage of staples that go up with a staple ball will be quite small until the total number of staples in a bowl is about a hundred, and then starts to increase to something close enough to 100%. Does any logical curve follow from this? And if so, which one? Anyway, this is a wonderful observation!
Yonkou : Very beautiful work. I wonder if the shape of the bowl plays a role.
I really understand the flat-plate experiment ... but did you add staples to the tops of the previous ones (which puts pressure when you do this in the bowl)? It is also interesting what would happen if we added them in a more limited container, say in a test tube.
Unekdoud : I think you should consider doing this with various office equipment, say with paper clips. Also, does the size of the stapler play a role?
Mix and match different types of them to form "alloys". If you view them as impurities in ice, there could be a definite significant effect on the structure. Is there an analogue of ice freezing temperature? What are the changes in density?
Sure, the size of the bowl matters. There is probably the possibility of making a giant component in a nonconvex form. As for the structure itself, you might want to consider actually displaying it as a graph in order to study the properties of subgraphs and cycles, as well as such things as the density of vertices. You can add a little glue to preserve the structure and make it easier to observe. Will the properties of the graph change if another method is used to create a giant component, such as using a magnet or magnetized scissors, to stir up the structure? How would this change if the staples were immersed in oil? What if they heat or cool in the middle of the process? What about vibrations at different frequencies? In terms of the size of the component, you may want to continue to add staples to see how large it can grow. Is it possible to combine the two components? And where can this be applied in addition to physics and chemistry? You can also recreate this experiment in the context of a social network. Similar effects will then be observed at different scales, or may be completely different.
Brian : Thank you Barry and Yonkou and Unekdoud for raising some interesting questions and suggesting further directions for research. Before I say anything else, I would like to point out that this is one of those rare cases in experimental science where anyone can play. Materials are readily available. You do not need an NSF grant to fund the study (although I assume that we could seek funding from office supply stores). At any cost: Grab a stapler and join. In the spirit of scientific cooperation and the zealous pursuit of truth, I am ready to share my supply of brackets used. Barry asks about the appearance of clusters in small sets of clips. I do not know how it is. With Erdős-Rényi graphs, known results are strictly valid only within an infinite N, but in practice infinity is quite rare in graph theory.
Unekdoud asks about the largest reachable clusters. Again, I do not know, but, of course, there must be a physical limit. At some point, the weight of the cluster exceeds the force of the bracket on which everything is held.
With regard to open questions about the shape of the bowl, the manner of stirring, the size of staples, etc.: besides the fact that these factors are important, we do not have a system that would lead to a clear analysis. I would prefer to get out of this chaotic world of metal brackets and go into the field of modeling, where we can computationally simulate and solve mathematically.
But, of course, I do not have such a model.
Finally about the clips. This is the territory of the American scientist colleague Henry Petroski. He wrote a book about it and let it remain his area.
Kevembuangga : I think this kind of “research” is deeply idiotic, but I am sincerely grateful that some people do it, just as I am grateful to people addicted to video games for successfully developing high-performance processor.
Ben : The first thing I thought about when you started talking about random graphs is that the “flat” part of the bracket should be the top and the “ends” should be the edges — in the end, all the edges form the “ties” that you described when discussed water molecules. The bonds between the edges are formed randomly, because the brackets are placed in a bowl or mixed around a bowl or something else. Then the change from 2 to 3 dimensions, from the surface to the bowl, changes the probability that a random link is formed between any two vertices. You need to think about how exactly, but apparently on the surface, the expected number of links is less than n / 2, while in a bowl it is more.
Jess : My thought is that the stapler as a whole is the top and edge formed when the two brackets engage each other. This seems simpler than the proposed merge process. We do not expect that the concept of an edge is more in the connection between two objects than in a rough physical analogue?
Stephan Mertens says: I assume that a kind of entropic ratchet mechanism (at least partially) is responsible for the formation of a giant component: there are many ways that two brackets can get caught but this requires that a coordinated movement separates a pair of connected staples. And I think the same argument applies to the power cords in your drawer, which always form a giant knot.
Publishing support - Edison company, which develops a billing system for providers , as well as develops software for tax reporting over the Internet .

An unnecessary product of my document scanning project is a bunch of extracted clips.
')
The other day I made a discovery: if you grab one of the discarded staples and lift it, a whole ball of tangled twisted metal will rise after it, leaving only a couple of staples at the bottom of the bowl. When I noticed this, I first thought, “Hm, this is funny.” Then "Oh, of course: Erdős-Rényi." And the third thought ... well, I'm still working on it, and also on the fourth, fifth and sixth.

Erdős and Rényi are Paul Erdős and Alfréd Rényi, who wrote a great work on the “Evolution of Random Graphs” 50 years ago (Publications of the Mathematical Institute of the Hungarian Academy of Sciences, 1960, 5: 17–61). Their article was not quite the debut appearance of random graphs in mathematical literature, but is considered the original origin of the theory.
In one version of the Erdős-Rényi process, you start with a set of isolated vertices n and then add random edges one by one; In particular, at each stage, you select any two vertices from among all the pairs that are no longer connected, and then draw an edge between them.
It turns out that a dramatic change in the nature of graphs occurs when the number of faces reaches n / 2. Below this threshold, a graph consists of many small, isolated components; above n / 2, the fragments merge into one giant component, which includes almost all the vertices.
“The birth of the giant component” was later described in more detail in an even larger article - it covered the entire question of random structures and algorithms (1993, 4: 233-358) and was written by Swante Janson, Donald Knuth, Tomasz Lutsaka and Boris Pittel.
What made me think about the connection between the Erdős-Rényi graphs and the clew? In my mind there was something like a long, straight, middle part of the bracket corresponds to the edge of the graph, and the curved parts that can interlock with each other are the vertices. Thus, one bracket is a graph consisting of two vertices connected along one edge. When two brackets are connected, their two vertices merge, and a connected graph of three vertices and two edges remains. Since each bracket gives one edge and at most two vertices to a graph, the number of edges must be at least half the number of vertices. Thus, the graph always exceeds the threshold when a giant component is formed, according to Erdős and Rényi.
With the computational part of this analysis, everything seems clear, but I am afraid that the rest is not so easy to understand. Regardless of what happens in the staple ball, the evolution of the system is not well modeled by the Erdős-Rényi process, which adds faces to a fixed set of vertices. Instead, each bracket gives 2 faces and 2 vertices.
The tipping point that makes a bundle of staples stick together is the merging of vertices when braces are held together; There is no such merger in the Erdős-Rényi process. The main problem here is that the Erdős-Rényi graphs are purely topological - there is no concept of distance, and any two vertices can have an edge connecting them. But the bracket graph has important geometric constraints. Two vertices can be connected by an edge only if the distance between them is approximately equal to the length of the bracket.
The geometric structure involves attempts to build various types of models - perhaps, that describes the molecular structure of liquids and solids. Water molecules, for example, are linked to each other by a network of hydrogen bonds; each hydrogen atom in one molecule can have a bond with the oxygen atom of another molecule. But connections cannot extend to arbitrary distances; they spread only between neighboring molecules. As a result, a three-dimensional structure was obtained, the main motive of which is a tetrahedron with an oxygen atom in the center and hydrogen atoms in the four corners. (There is also a diagram of a two-dimensional model, known as ice area). We can imagine how something like this happens with brackets, where two bent ends can form hydrogen bonds as a bond with other nearby braces.
But with such chemical elements there is also a problem. The atoms have a fixed valence (more or less - let's not find fault); in water, for example, each hydrogen atom can form a hydrogen bond with only one oxygen atom. But we have no reason to believe that the hooked ends of the staples can hook only one edge of the other bracket. In fact, if such a restriction existed, then the brackets could form only chains and rings, not dense clusters. On close examination of a cluster of brackets, it is easy to find places where three or more brackets are linked together at the same point. Carefully peering deep into the staple clusters, I found a staple, to which at least six other clips were clinging.
Another physical process that could provide a model for the main graph is aggregation of limited distribution. This is the mechanism responsible for the filigree pattern.

It is produced by sticky particles that drift randomly until they stumble onto the ground or touch another particle that is already in contact (directly or indirectly) with the base.
Another factor to consider is the fact that spatial dimensions are undoubtedly important here. On the one hand, it just gives more opportunities to maneuver in three dimensions, more opportunities to cling to a neighbor. But specifically in the case of staples, there is another reason: being chained to a plane, it is difficult for them to connect.

Scattered on a flat board, they refuse to fold, even when spinning vigorously. The reason, apparently, is that safe joints are formed only when the brackets can turn 90 degrees and mate. In this regard, it is important that brackets are used, quite diverse in shape, with hooked ends bent about 180 degrees during the binding process and which basically retained an angle of more than 90 degrees after they were pulled out of the paper.
I wondered how the shiny new braces would behave and I conducted an experiment (Materials and methods: 630 Stanley Bostitch chisel-point staples, model SBS191 / 4CP, freshly dispensed from an open-jaw Swingline stapler.)
I was, to put it mildly, surprised by the result. Although the stack of staples was somewhat looser and more subtle, the gist really wasn't that different. Again we witness the birth of a giant component.
Comments
Barry Cipra : It might be worthwhile to repeat the experiment with new braces, pausing every time you add braces (say every 10 or 20 brackets), shaking what is already in the bowl, and then watch how a large congestion forms when you take one of the brackets. Perhaps it would be nice to repeat the shake and pause between adding staples several times and watch the statistics. I assume that the (average) percentage of staples that go up with a staple ball will be quite small until the total number of staples in a bowl is about a hundred, and then starts to increase to something close enough to 100%. Does any logical curve follow from this? And if so, which one? Anyway, this is a wonderful observation!
Yonkou : Very beautiful work. I wonder if the shape of the bowl plays a role.
I really understand the flat-plate experiment ... but did you add staples to the tops of the previous ones (which puts pressure when you do this in the bowl)? It is also interesting what would happen if we added them in a more limited container, say in a test tube.
Unekdoud : I think you should consider doing this with various office equipment, say with paper clips. Also, does the size of the stapler play a role?
Mix and match different types of them to form "alloys". If you view them as impurities in ice, there could be a definite significant effect on the structure. Is there an analogue of ice freezing temperature? What are the changes in density?
Sure, the size of the bowl matters. There is probably the possibility of making a giant component in a nonconvex form. As for the structure itself, you might want to consider actually displaying it as a graph in order to study the properties of subgraphs and cycles, as well as such things as the density of vertices. You can add a little glue to preserve the structure and make it easier to observe. Will the properties of the graph change if another method is used to create a giant component, such as using a magnet or magnetized scissors, to stir up the structure? How would this change if the staples were immersed in oil? What if they heat or cool in the middle of the process? What about vibrations at different frequencies? In terms of the size of the component, you may want to continue to add staples to see how large it can grow. Is it possible to combine the two components? And where can this be applied in addition to physics and chemistry? You can also recreate this experiment in the context of a social network. Similar effects will then be observed at different scales, or may be completely different.
Brian : Thank you Barry and Yonkou and Unekdoud for raising some interesting questions and suggesting further directions for research. Before I say anything else, I would like to point out that this is one of those rare cases in experimental science where anyone can play. Materials are readily available. You do not need an NSF grant to fund the study (although I assume that we could seek funding from office supply stores). At any cost: Grab a stapler and join. In the spirit of scientific cooperation and the zealous pursuit of truth, I am ready to share my supply of brackets used. Barry asks about the appearance of clusters in small sets of clips. I do not know how it is. With Erdős-Rényi graphs, known results are strictly valid only within an infinite N, but in practice infinity is quite rare in graph theory.
Unekdoud asks about the largest reachable clusters. Again, I do not know, but, of course, there must be a physical limit. At some point, the weight of the cluster exceeds the force of the bracket on which everything is held.
With regard to open questions about the shape of the bowl, the manner of stirring, the size of staples, etc.: besides the fact that these factors are important, we do not have a system that would lead to a clear analysis. I would prefer to get out of this chaotic world of metal brackets and go into the field of modeling, where we can computationally simulate and solve mathematically.
But, of course, I do not have such a model.
Finally about the clips. This is the territory of the American scientist colleague Henry Petroski. He wrote a book about it and let it remain his area.
Kevembuangga : I think this kind of “research” is deeply idiotic, but I am sincerely grateful that some people do it, just as I am grateful to people addicted to video games for successfully developing high-performance processor.
Ben : The first thing I thought about when you started talking about random graphs is that the “flat” part of the bracket should be the top and the “ends” should be the edges — in the end, all the edges form the “ties” that you described when discussed water molecules. The bonds between the edges are formed randomly, because the brackets are placed in a bowl or mixed around a bowl or something else. Then the change from 2 to 3 dimensions, from the surface to the bowl, changes the probability that a random link is formed between any two vertices. You need to think about how exactly, but apparently on the surface, the expected number of links is less than n / 2, while in a bowl it is more.
Jess : My thought is that the stapler as a whole is the top and edge formed when the two brackets engage each other. This seems simpler than the proposed merge process. We do not expect that the concept of an edge is more in the connection between two objects than in a rough physical analogue?
Stephan Mertens says: I assume that a kind of entropic ratchet mechanism (at least partially) is responsible for the formation of a giant component: there are many ways that two brackets can get caught but this requires that a coordinated movement separates a pair of connected staples. And I think the same argument applies to the power cords in your drawer, which always form a giant knot.
More materials:
- Giant component
- The birth of the giant component
- Connectedness G (n, p), giant component, characteristic numbers G (n, p)
- Lecture 9 - A theorem on the appearance of a giant component in a random graph
- Systems biology - M. Gelfand's networks "Comparative genomics" BB 4 course. - presentation
- From Cycles to Giant Components, a Socially-guided Tour
- NetLogo Models Library: Sample Models / Networks
Publishing support - Edison company, which develops a billing system for providers , as well as develops software for tax reporting over the Internet .
Source: https://habr.com/ru/post/317750/
All Articles