The Tale of Lost Time
To be honest, not quite a fairy tale, but a harsh life. But time is lost, the present is completely, albeit to good use. It all started quite by accident. On one site, one intelligent comrade wrote a post about Euler 's hypothesis . The point is quite simple. Euler's hypothesis states that for any natural number n> 2, no nth power of a natural number can be represented as the sum of (n-1) nth powers of other natural numbers. That is, the equations:
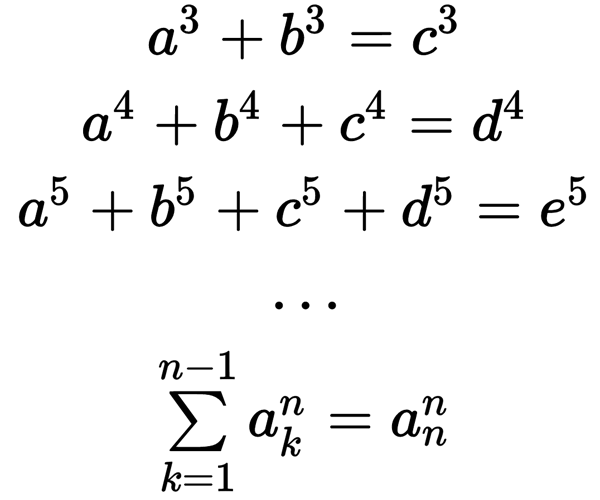
do not have a solution in natural numbers.
Well, actually the way it was until 1966 ...
So far L. Lander (LJ Lander), T. Parkin (TR Parkin) and J. Selfridge (JL Selfridge) did not find the first counterexample for n = 5. And they did it on a supercomputer of that time - CDC 6600 , developed under the command of a not unknown Seymour Roger Cray (Seymour Roger Cray) and had this supercomputer performance as much as 3 MFLOPS. Their scientific work looked like this:
')

That is, by a simple search on a supercomputer, they found numbers of degree 5, which disproved Euler's hypothesis: 27 5 + 84 5 + 110 5 + 133 5 = 144 5 .
And everything would be fine, but another smart comrade asked : "I wonder, but can any programmer write out the code for a super-modern i5 to search for more such coincidences? ... ".
As you can see, the offer worked like a red rag. The first decision was quite beautiful and written with the mind. The bottom line is that we first consider the fifth degrees for 1-N numbers, put them in a table and recursively start looking at the bottom of the four terms of the fifth degrees, looking in the table for the sum of the resulting values. If found - this is the solution (the index in the table will be a number, the degree of which we have found).
This is the first version of 2Alias :
And as it usually happens, I thought, can it be faster? At the same time, people have a question, what will happen if you check C # in this case. I rewrote the solution in C # on the forehead and the program showed approximately the same result in time. Already interesting! But we will still optimize C ++. After all then all is easy for transferring to C #.
The first thing that came to mind was to remove recursion. Well, just enter 4 variables and we will sort them out with the increment of the older ones when the younger ones overflow.
And then the result became worse. After all, we will meet many identical amounts, most of which bypass the recursive algorithm. Suppose we have numbers from 1 to 3, we will iterate them:
111
112
113
121 <- already been!
122
123
131 <- already been!
132 <- already been!
133
...
So I’ll have to watch combinatorics, but it didn’t help me much, since I don’t have enough knowledge on this topic, I had to write out about the same example on a piece of paper and think. And the solution was found: with the increment of the higher digits, you do not need to reset the younger ones to the very minimum, but assign the value of the older ones to all the younger ones - this way we cut off the excess.
The index increase code has become:
Hooray! And immediately a little faster. But what does the profiler tell us? Most of the time we sit in unordered_map.find ...
I start to remember search algorithms and various knowledge (up to the demoscene). And what if before checking in unordered_map somehow quickly cut off some of the unnecessary?
So there was another array, already bit (bitset). Since we don’t put numbers into it (they are too big), we’ll have to quickly make a hash of a power, bring it to the number of bits in the array and mark there. All this must be done when constructing a table of degrees. In the process of writing, it turned out that std :: bitset is a little slower than a simple array and minimal logic that I sketched. Well, okay, this is nonsense. But in general, the acceleration was significant, about two times.
A lot of experimenting with the size of the bitset and the complexity of the hash made it clear that by and large only memory affects, and for different N differently and a large degree of filtering of calls to unordered_map.find is better only up to a certain limit.
It looked like this:
Then there was problem number two. The first example from the distant 1966 had the maximum number of 144 5 (61 917 364 224), and the second (2004) already 85359 5 (4 531 548 087 264 753 520 490 799) - the numbers cease to fit 64 bits ...
We go the easiest way: take boost :: multiprecision :: uint128 - that’s enough for us for a long time! This is due to the fact that I use MS CL, but it just does not support uint128, like all other compilers. By the way, during the search for a solution to the problem of uint128 and compilers, I also found out about the posh site - Compiler Explorer . Directly online, you can compile the code with all popular compilers of different versions and see what they are translating into it (assembler), and with different compilation flags. MS CL is also there, but on the beta site. And besides C ++, there is Rust , D and Go . Actually, it became clear from the code that MS CL does not understand 128 compound integers at all, all compilers translate the multiplication of two 64-bit into 128-bit structure for three multiplications, and MS CL for four. But back to the code.
With boost :: multiprecision :: uint128, performance dropped 25 times. And this is somehow completely wrong, because in theory there should be no more than 3 times. It's funny that the performance of the decimal type C # has dropped by the same amount (although it is not quite integer, but its 96bit mantissa). And preliminary filtering of calls to the Dictionary (a kind of unordered_map from STL) works well, the acceleration is very noticeable.
Well, then you know, it became a shame. So much has already been done and everything is in vain. So we will reinvent the wheel! That is, the simple data type is uint128. In fact, we only need assignment, comparison, multiplication and addition. Not so difficult, but the process at the beginning went wrong, because at first I took up the multiplication and it came to the use of the assembler. There is nothing to be proud of; intrinsics showed themselves best of all. Why did the process go wrong? And multiplication is not important for us. After all, multiplication is involved only at the stage of calculating the degree table and does not participate in the main cycle. Just in case, the source file has a multiply file on an assembler - it will suddenly come in handy.
With its uint128, performance also, of course, slipped, but only by 30% and that’s great! Joy is full, but we do not forget the profiler. But what if you completely remove unordered_map and make a bitor similar to unordered_map from a self-defined bitset? That is, after calculating the amount hash, we can already use this number as an index in another table (unordered_map is not needed then).
Since the project was completely frivolous and did not carry any payload, I saved all the ways of searching, searching and different values through a terrible set of defines and mainType just one of them - this is the type where the degree of the number is written to replace it when changing only once code. Already at this stage, all tests can be performed with uint64, uint128 and boost :: multiprecision :: uint128, depending on the define - it turns out very interesting.
And you know, the introduction of your map has helped! But not for long. After all, it is clear that the map is not just so invented and used wherever possible. Experiments - this, of course, confirm. With a certain N (closer to 1,000,000), when all the algorithms are already inhibited, the bare map (without a prior bitset) already bypasses the samopisny analog and saves only a significant increase in the bit array and the array where our values of degrees and numbers are stored, and this is a huge amount of memory. An approximate multiplier of about N * 192, that is, for N = 1 000 000 we need more than 200mb. And then even more. At this point, it was not yet understood why the speed drops as the array of degrees grows, and I continued to look for bottlenecks with the profiler.
While thinking was going on, I made all the tried and tested methods switchable. For you never know what.
One of the latest optimizations turned out to be simple, but effective. The speed of the C ++ version has already exceeded 400 000 000 searches per second for 64 bits (with N = 500), 300 000 000 searches for 128 bits and only 24 000 000 for 128 bits from boost, and almost everything could affect the speed. If you translate in GB, then the reading is about 20GB per second. Well, maybe I was wrong somewhere ...
Suddenly it became clear that it was not necessary to recalculate the entire amount on each pass and you can enter an intermediate one. Instead of three additions there will be one. And to recalculate the intermediate only when increasing the high-order digits. For larger types, this is of course more pronounced.
Here, the task was beginning to bother, since it was no longer possible and I started the C # version. Everything moved there. I found a ready-made UInt128, written by another person - about as simple as mine for C ++. And, of course, the speed jumped strongly. The difference was less than half compared to 64 bits. And this is another VS2013 for me, that is, not roslyn (can it be faster?).
But samopisny map loses in all articles Dictionary. Apparently checking the boundaries of arrays make themselves felt, for increasing the memory does not give anything.
Then it went completely nonsense, there was even an attempt to optimize the addition of intrinsics, but the pure C ++ version turned out to be the fastest. For some reason, I could not get the inline assembly code.
And yet I constantly did not let go the feeling that I did not see something. Why does everything start to slow down as the array grows? When N = 1 000 000 performance drops by 30 times. Comes to the CPU cache. I even tried the prefetch intrinsic, the result is zero. The idea came to cache a part of the array being scanned, but at 1,000,000 values (20 bytes) it looks somehow stupid. And then the full picture begins to emerge.
Since the numbers are 4, there are 4 indices that take values from the table. The table is of constantly increasing values and the sum of all four degrees is constantly increasing (until the switching of the highest indices). And the difference of degrees becomes more and more.
2 5 is 32, and 3 5 is already 243. And what if we search directly in the same array of calculated degrees with the usual linear search, first setting the initial value to the largest index and keeping the index of the last smaller value found than our sum (the next one will be more) and use this saved index as a starting point in the next search, because the values will not change much ... Bingo!
What is the result?
The speed at small values of N is slightly inferior to the samopisny map, but as soon as N grows, the speed of work even starts to grow! After all, the intervals between the powers of large N grow the farther, the more and the linear search works less and less! The complexity is better than O (1).
So much for the loss of time. And why? Do not rush to the embrasure, sit down - think. As it turned out, the fastest algorithm is a linear search and no map / bitset is needed. But, of course, this is a very interesting experience.
Habr loves source codes and I have them . In commits, you can even see the history of the "struggle". There are both versions of C ++ and C #, in which this trick, of course, works just as well. Projects, though invested in one another, but, of course, not connected.
The sources are terrible, there are defaults at the beginning, where you can set the main value (uint64, uint128, boost :: uin128 / decimal (for C #), the library can be switched std / boost (boost :: unordered_map turned out to be faster than std :: unordered_map by about 10% The search algorithm is also selected (though now I see that the preliminary filter for unordered_map in C ++ version did not survive the edits, but it is in commits and in C # version) unordered_map, self-defined bitset and range (last option).
Here is such a fairy tale and a lesson to me. And maybe someone else will be interested. After all, a lot of what values have not yet found ...

* k / f Tale of Lost Time, 1964.
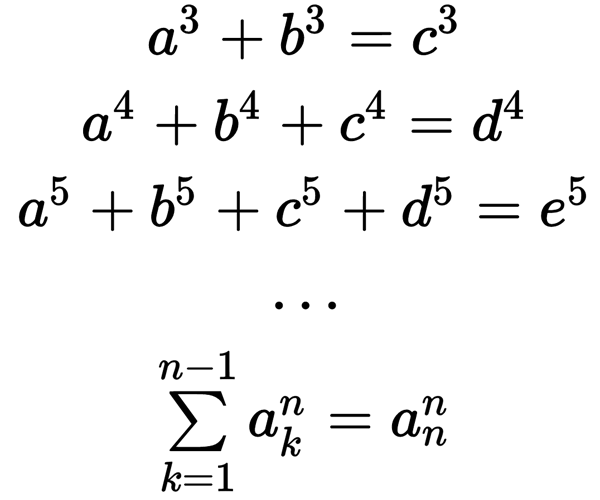
do not have a solution in natural numbers.
Well, actually the way it was until 1966 ...
So far L. Lander (LJ Lander), T. Parkin (TR Parkin) and J. Selfridge (JL Selfridge) did not find the first counterexample for n = 5. And they did it on a supercomputer of that time - CDC 6600 , developed under the command of a not unknown Seymour Roger Cray (Seymour Roger Cray) and had this supercomputer performance as much as 3 MFLOPS. Their scientific work looked like this:
')

That is, by a simple search on a supercomputer, they found numbers of degree 5, which disproved Euler's hypothesis: 27 5 + 84 5 + 110 5 + 133 5 = 144 5 .
And everything would be fine, but another smart comrade asked : "I wonder, but can any programmer write out the code for a super-modern i5 to search for more such coincidences? ... ".
As you can see, the offer worked like a red rag. The first decision was quite beautiful and written with the mind. The bottom line is that we first consider the fifth degrees for 1-N numbers, put them in a table and recursively start looking at the bottom of the four terms of the fifth degrees, looking in the table for the sum of the resulting values. If found - this is the solution (the index in the table will be a number, the degree of which we have found).
This is the first version of 2Alias :
#include <iostream> #include <algorithm> #include <stdlib.h> #include <vector> #include <unordered_map> using namespace std; typedef long long LL; const int N = 250; LL p5(int x) { int t = x * x; return t * (LL) (t * x); } vector<LL> p; std::unordered_map<LL, int> all; int res[5]; void rec(int pr, LL sum, int n) { if (n == 4) { if (all.find(sum) != all.end()) { cout << "Ok\n"; res[4] = all[sum]; for (int i = 0; i < 5; ++i) cout << res[i] << " "; cout << "\n"; exit(0); } return; } for (int i = pr + 1; i < N; ++i) { res[n] = i; rec(i, sum + p[i], n + 1); } } int main() { for (int i = 0; i < N; ++i) { p.push_back(p5(i)); all[p.back()] = i; } rec(1, 0, 0); return 0; } And as it usually happens, I thought, can it be faster? At the same time, people have a question, what will happen if you check C # in this case. I rewrote the solution in C # on the forehead and the program showed approximately the same result in time. Already interesting! But we will still optimize C ++. After all then all is easy for transferring to C #.
The first thing that came to mind was to remove recursion. Well, just enter 4 variables and we will sort them out with the increment of the older ones when the younger ones overflow.
// N - 1 - N 5 // powers - // all = unordered_map< key= , value= > uint32 ind0 = 0x02; // 2 uint32 ind1 = 0x02; uint32 ind2 = 0x02; uint32 ind3 = 0x02; uint64 sum = 0; while (true) { sum = powers[ind0] + powers[ind1] + powers[ind2] + powers[ind3]; if (all.find(sum) != all.end()) { // - !! foundVal = all[sum]; ... } // ++ind0; if (ind0 < N) { continue; } else { ind0 = 0x02; ++ind1; } if (ind1 >= N) { ind1 = 0x02; ++ind2; } if (ind2 >= N) { ind2 = 0x02; ++ind3; } if (ind3 >= N) { break; } } And then the result became worse. After all, we will meet many identical amounts, most of which bypass the recursive algorithm. Suppose we have numbers from 1 to 3, we will iterate them:
111
112
113
121 <- already been!
122
123
131 <- already been!
132 <- already been!
133
...
So I’ll have to watch combinatorics, but it didn’t help me much, since I don’t have enough knowledge on this topic, I had to write out about the same example on a piece of paper and think. And the solution was found: with the increment of the higher digits, you do not need to reset the younger ones to the very minimum, but assign the value of the older ones to all the younger ones - this way we cut off the excess.
The index increase code has become:
... // ++ind0; if (ind0 < N) { continue; } else { ind0 = ++ind1; } if (ind1 >= N) { ind0 = ind1 = ++ind2; } if (ind2 >= N) { ind0 = ind1 = ind2 = ++ind3; } if (ind3 >= N) { break; } Hooray! And immediately a little faster. But what does the profiler tell us? Most of the time we sit in unordered_map.find ...
I start to remember search algorithms and various knowledge (up to the demoscene). And what if before checking in unordered_map somehow quickly cut off some of the unnecessary?
So there was another array, already bit (bitset). Since we don’t put numbers into it (they are too big), we’ll have to quickly make a hash of a power, bring it to the number of bits in the array and mark there. All this must be done when constructing a table of degrees. In the process of writing, it turned out that std :: bitset is a little slower than a simple array and minimal logic that I sketched. Well, okay, this is nonsense. But in general, the acceleration was significant, about two times.
A lot of experimenting with the size of the bitset and the complexity of the hash made it clear that by and large only memory affects, and for different N differently and a large degree of filtering of calls to unordered_map.find is better only up to a certain limit.
It looked like this:
... // if (findBit(sum)) { // map, - - if (all.find(sum) != all.end()) { // ! } } // ... Then there was problem number two. The first example from the distant 1966 had the maximum number of 144 5 (61 917 364 224), and the second (2004) already 85359 5 (4 531 548 087 264 753 520 490 799) - the numbers cease to fit 64 bits ...
We go the easiest way: take boost :: multiprecision :: uint128 - that’s enough for us for a long time! This is due to the fact that I use MS CL, but it just does not support uint128, like all other compilers. By the way, during the search for a solution to the problem of uint128 and compilers, I also found out about the posh site - Compiler Explorer . Directly online, you can compile the code with all popular compilers of different versions and see what they are translating into it (assembler), and with different compilation flags. MS CL is also there, but on the beta site. And besides C ++, there is Rust , D and Go . Actually, it became clear from the code that MS CL does not understand 128 compound integers at all, all compilers translate the multiplication of two 64-bit into 128-bit structure for three multiplications, and MS CL for four. But back to the code.
With boost :: multiprecision :: uint128, performance dropped 25 times. And this is somehow completely wrong, because in theory there should be no more than 3 times. It's funny that the performance of the decimal type C # has dropped by the same amount (although it is not quite integer, but its 96bit mantissa). And preliminary filtering of calls to the Dictionary (a kind of unordered_map from STL) works well, the acceleration is very noticeable.
Well, then you know, it became a shame. So much has already been done and everything is in vain. So we will reinvent the wheel! That is, the simple data type is uint128. In fact, we only need assignment, comparison, multiplication and addition. Not so difficult, but the process at the beginning went wrong, because at first I took up the multiplication and it came to the use of the assembler. There is nothing to be proud of; intrinsics showed themselves best of all. Why did the process go wrong? And multiplication is not important for us. After all, multiplication is involved only at the stage of calculating the degree table and does not participate in the main cycle. Just in case, the source file has a multiply file on an assembler - it will suddenly come in handy.
friend uint128 operator*(const uint128& s, const uint128& d) { // intristic use uint64 h = 0; uint64 l = 0; uint64 h2 = 0; l = _mulx_u64(dl, sl, &h); h += _mulx_u64(dl, sh, &h2); h += _mulx_u64(dh, sl, &h2); return uint128( h, l); } With its uint128, performance also, of course, slipped, but only by 30% and that’s great! Joy is full, but we do not forget the profiler. But what if you completely remove unordered_map and make a bitor similar to unordered_map from a self-defined bitset? That is, after calculating the amount hash, we can already use this number as an index in another table (unordered_map is not needed then).
// map boost::container::vector<CompValue*> setMap[ SEARCHBITSETSIZE * 8 ]; ... // ComValue struct CompValue { ... mainType fivePower; uint32 number; }; // map inline uint32 findBit(mainType fivePower) { uint32 bitval = (((uint32)((fivePower >> 32) ^ fivePower))); bitval = (((bitval >> 16) ^ bitval) & SEARCHBITSETSIZEMASK); uint32 b = 1 << (bitval & 0x1F); uint32 index = bitval >> 5; if((bitseta[index] & b) > 0) { for (auto itm : setMap[bitval]) { if (itm->fivePower == fivePower) { return itm->number; } } } return 0; } Since the project was completely frivolous and did not carry any payload, I saved all the ways of searching, searching and different values through a terrible set of defines and mainType just one of them - this is the type where the degree of the number is written to replace it when changing only once code. Already at this stage, all tests can be performed with uint64, uint128 and boost :: multiprecision :: uint128, depending on the define - it turns out very interesting.
And you know, the introduction of your map has helped! But not for long. After all, it is clear that the map is not just so invented and used wherever possible. Experiments - this, of course, confirm. With a certain N (closer to 1,000,000), when all the algorithms are already inhibited, the bare map (without a prior bitset) already bypasses the samopisny analog and saves only a significant increase in the bit array and the array where our values of degrees and numbers are stored, and this is a huge amount of memory. An approximate multiplier of about N * 192, that is, for N = 1 000 000 we need more than 200mb. And then even more. At this point, it was not yet understood why the speed drops as the array of degrees grows, and I continued to look for bottlenecks with the profiler.
While thinking was going on, I made all the tried and tested methods switchable. For you never know what.
One of the latest optimizations turned out to be simple, but effective. The speed of the C ++ version has already exceeded 400 000 000 searches per second for 64 bits (with N = 500), 300 000 000 searches for 128 bits and only 24 000 000 for 128 bits from boost, and almost everything could affect the speed. If you translate in GB, then the reading is about 20GB per second. Well, maybe I was wrong somewhere ...
Suddenly it became clear that it was not necessary to recalculate the entire amount on each pass and you can enter an intermediate one. Instead of three additions there will be one. And to recalculate the intermediate only when increasing the high-order digits. For larger types, this is of course more pronounced.
mainType sum = 0U, baseSum = 0U; baseSum = powers[ind1] + powers[ind2] + powers[ind3]; while(true) { sum = baseSum + powers[ind0]; ... // refresh without ind0 baseSum = powers[ind1] + powers[ind2] + powers[ind3]; } Here, the task was beginning to bother, since it was no longer possible and I started the C # version. Everything moved there. I found a ready-made UInt128, written by another person - about as simple as mine for C ++. And, of course, the speed jumped strongly. The difference was less than half compared to 64 bits. And this is another VS2013 for me, that is, not roslyn (can it be faster?).
But samopisny map loses in all articles Dictionary. Apparently checking the boundaries of arrays make themselves felt, for increasing the memory does not give anything.
Then it went completely nonsense, there was even an attempt to optimize the addition of intrinsics, but the pure C ++ version turned out to be the fastest. For some reason, I could not get the inline assembly code.
And yet I constantly did not let go the feeling that I did not see something. Why does everything start to slow down as the array grows? When N = 1 000 000 performance drops by 30 times. Comes to the CPU cache. I even tried the prefetch intrinsic, the result is zero. The idea came to cache a part of the array being scanned, but at 1,000,000 values (20 bytes) it looks somehow stupid. And then the full picture begins to emerge.
Since the numbers are 4, there are 4 indices that take values from the table. The table is of constantly increasing values and the sum of all four degrees is constantly increasing (until the switching of the highest indices). And the difference of degrees becomes more and more.
2 5 is 32, and 3 5 is already 243. And what if we search directly in the same array of calculated degrees with the usual linear search, first setting the initial value to the largest index and keeping the index of the last smaller value found than our sum (the next one will be more) and use this saved index as a starting point in the next search, because the values will not change much ... Bingo!
What is the result?
uint32 lastRangeIndex = 0; // inline uint32 findInRange(mainType fivePower, uint32 startIndex) { while (startIndex < N) { lastRangeIndex = startIndex; if (powers[startIndex] > fivePower) { return 0; } if (powers[startIndex] == fivePower) { return startIndex; } ++startIndex; } return 0; } ... // baseSum = powers[ind1] + powers[ind2] + powers[ind3]; while (true) { sum = baseSum + powers[ind0]; foundVal = findInRange( sum, lastRangeIndex); if (foundVal > 0) { // ! } // ++ind0; if (ind0 < N) { continue; } else { ind0 = ++ind1; } if (ind1 >= N) { ind0 = ind1 = ++ind2; } if (ind2 >= N) { ind0 = ind1 = ind2 = ++ind3; } if (ind3 >= N) { break; } // lastRangeIndex = 0x02; if (ind1 > lastRangeIndex) { lastRangeIndex = ind1; } if (ind2 > lastRangeIndex) { lastRangeIndex = ind2; } if (ind3 > lastRangeIndex) { lastRangeIndex = ind3; } // refresh without ind0 baseSum = powers[ind1] + powers[ind2] + powers[ind3]; } The speed at small values of N is slightly inferior to the samopisny map, but as soon as N grows, the speed of work even starts to grow! After all, the intervals between the powers of large N grow the farther, the more and the linear search works less and less! The complexity is better than O (1).
So much for the loss of time. And why? Do not rush to the embrasure, sit down - think. As it turned out, the fastest algorithm is a linear search and no map / bitset is needed. But, of course, this is a very interesting experience.
Habr loves source codes and I have them . In commits, you can even see the history of the "struggle". There are both versions of C ++ and C #, in which this trick, of course, works just as well. Projects, though invested in one another, but, of course, not connected.
The sources are terrible, there are defaults at the beginning, where you can set the main value (uint64, uint128, boost :: uin128 / decimal (for C #), the library can be switched std / boost (boost :: unordered_map turned out to be faster than std :: unordered_map by about 10% The search algorithm is also selected (though now I see that the preliminary filter for unordered_map in C ++ version did not survive the edits, but it is in commits and in C # version) unordered_map, self-defined bitset and range (last option).
Here is such a fairy tale and a lesson to me. And maybe someone else will be interested. After all, a lot of what values have not yet found ...

* k / f Tale of Lost Time, 1964.
Source: https://habr.com/ru/post/317588/
All Articles