Neural networks on JS. Creating a network from scratch

Neural networks are now in trend. Every day we read about how they learn to write comments on the Internet, bargain in the markets, handle photos. The list is endless. When I first looked at the scale of the code that sets it in motion, I was scared and wanted not to see these sources anymore.

But the innate curiosity and enthusiasm brought me to the point that I became one of the developers of Synaptic - a framework project for building neural networks on JS with 3k + stars on GitHub. Now we are working with the author of the framework to create Synaptic 2.0 with GPU and WebWorker acceleration and with the support of almost all the main features of any decent NN framework.

As a result, it turned out that neural networks are easy, they work on fairly simple principles that are easy to understand and reproduce. The most difficult task is learning, but almost always use ready-made algorithms for this, and copying them is not very difficult.

Proving is easy. Below in the article the implementation of a neural network from scratch without any libraries.

For a start - a little background.

At the end of October, I gave a report at the #ITsubbotnik event in St. Petersburg and began a topic that I decided to continue here. Let's talk about how to write from scratch neural network in JavaScript.

If you were on the first part of my speech or watched it on youtube , you can skip the next few paragraphs - this is a brief retelling of it.

What is a neural network?

The best of the definitions I heard from one sophisticated person at the conference. He said that neural networks are just a beautiful name that was invented, because it is more difficult to get a grant for the definition of the “chain of matrix operations”.

In general, this very accurately describes the real situation with neural networks. This is a cool and powerful technology, but the HYIP around it is more than real information. The same Google Brain that does things like “the neural network invented the encryption algorithm” is consistently ridiculed for them in the thematic communities, since there are no radically new ideas in such things, and they are made, first of all, to attract attention and public relations. the company.

To explain what a network is, you need to go a little distance.

From the point of view of Data Scientists (still there is the point of view of neuroscientists, for example) the neural network is one of the tools for modeling a physical process. And any of the modeling tools works as follows:

• we make a significant number of observations
• we collect key information for each of these observations
• from this information we get knowledge
• through this knowledge we find a solution

Linear dependence

As an example, you can take the metallurgy. Imagine that we have an alloy of 2 metals. If we take 80% of cast iron and 20% of aluminum (for example), a beam of such an alloy will break if one ton is pressed against it. If we take 70% + 30% - it will break if it presses 2 tons. 60% + 40% - 3 tons.

It can be assumed that the option 50% + 50% should withstand 4 tons. In life, everything works a little differently, but simplifying - you can imagine that it works that way.

In real life, this usually leads to the fact that a huge number of observations already exist, and on the basis of them you can build some kind of mathematical model that would give, for example, such an answer - what characteristics would a metal have from such and such components, for example.

One of the easiest and most effective tools is linear regression. The example above — where% in the alloy is directly proportional to the maximum load — is a linear regression.

In general, linear regression is as follows:

function predict(x1, x2, x3..., xN) { return weights.x1 * x1 + weights.x2 * x2 + ... + weights.xN * xN + weights.bias; } 

It is worth remembering the term "weight", weight. In further examples, it will also be used. The weight (or significance) of each parameter is called its significance in our predictive model — and both the neural network and linear regression are all models for prediction.

The weight of “bias”, or translated into Russian, “shift” is an additional parameter that characterizes the value at zero.

For example, in the well-known (albeit not very correct) formula "the correct weight should be equal to height - 100" - weight = height - 100 - bias is equal to -100, and the weight of growth - to one.

Nonlinear dependence

Sometimes there are situations when we need to find dependencies of higher orders.

One of the good examples to study is the dataset (dataset) of the Titanic with statistics on surviving people.

If you play with interactive visualization , you can see that on average women survived more. However, if you delve into the details, we note that among the crew and the third class - the survival rate was much less. To build a more accurate predictive model, we need to somehow write down in it - "if it is a woman and she is from class 1, then she had a + 10% chance of surviving."

The guys from science have proposed a simple scheme - to call such parameters additional features and use them in the original function. That is, to our x1, x2, x3, and so on, one more xN + 1 is added, which is 1 if it is a woman from the first class, and 0 if not. Then more and more parameters appear, and we begin to take all this into account in our calculations.

How can the function "if a condition , then 1, otherwise 0" be described in the language of mathematics?

If we solve the problem in the forehead, making an analogue of the ternary operator, then we will have a function, the schedule for which looks like this:

But you can get smarter, leaving a bunch of loopholes. The fact is that it is difficult to work with such a schedule. Because of the gap from it, it is impossible, for example, to take a derivative, or to perform a dozen more interesting tricks. Therefore, instead of such a "broken" function, continuous and continuously increasing functions are usually used, for example, sigmoid - 1 / (1 + Math.E ** -x) . It looks like this:

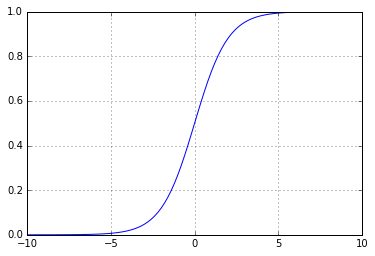
It works very similar - in -1 the value is close to 0, and in 1 it is close to 1, but we get more effective feedback: by the obtained value we can understand how close or far we are from the correct answer - unlike the original broken line a function by which we can only understand whether we answered correctly or were wrong: if we received 1 and expected 0, then we did not know how much we should move to the left on the schedule in order to get all the same 0.

This function is called the activation function.

As a result, we get a new parameter through the function of the form

 const activation_sigmoid = x => 1 / (1 + Math.exp(-x)); function predict(x1, x2, x3..., xN) { return activation_sigmoid( weights.x1 * x1 + weights.x2 * x2 + ... + weights.xN * xN + weights.bias); } 

This function is called the perceptron.

A perceptron is the simplest type of neural network, having no hidden layers. In a visual presentation, it looks something like this:

If you look at the picture from the article "neural network" on Wikipedia, then you can see a very large similarity:

And we come to the definition of a neural network in terms of implementation.

The classical neural network is just a chain of alternately linear and nonlinear transformations of input data. There are exceptions, but usually they just have a more cunning (read, non-linear) network structure.

In the simplest and most “canonical” case - not to mention image recognition or word processing - the neural network is a set of layers, each of which consists of neurons. Each of the neurons summarizes all the parameters from the previous layer with some weights specific to this neuron, and then passes the sum through the activation function.

If it seemed too complicated, just read further: in the code it looks much simpler.

Neural network in the code

With neural networks, the most popular example is the implementation of XOR , this is a kind of Hello World for data science learners.

The feature of XOR is that it is the simplest non-linear function — it cannot be implemented as a linear regression (read, you cannot draw a line through all the values).

Dataset for her looks like this:

 var data = [ {input: [0, 0], output: 0}, {input: [1, 0], output: 1}, {input: [0, 1], output: 1}, {input: [1, 1], output: 0}, ]; 

So, we need to somehow implement XOR exclusively using additions and a nonlinear function, which takes one number as input.

This is how the implementation looks like (so far without a neural network):

 var activation = x => x >= .5 ? 1 : 0; function xor(x1, x2) { var h1 = activation(-x1 + x2); var h2 = activation(+x1 - x2); return activation(h1 + h2); } 

Where h1 and h2 are hidden parameters.

Or, if you try to add weight, it turns out:

 var activation = x => x >= .5 ? 1 : 0; var weights = { x1_h1: -1, x1_h2: 1, x2_h1: 1, x2_h2: -1, bias_h1: 0, bias_h2: 0 } function xor(x1, x2) { var h1 = activation( weights.x1_h1 * x1 + weights.x2_h1 * x2 + weights.bias_h1); var h2 = activation( weights.x1_h2 * x1 + weights.x2_h2 * x2 + weights.bias_h2); return activation(h1 + h2); } 

What does our neural network function look like? Well, we replace weights with random values.

 var rand = Math.random; var weights = { i1_h1: rand(), i2_h1: rand(), bias_h1: rand(), i1_h2: rand(), i2_h2: rand(), bias_h2: rand(), h1_o1: rand(), h2_o1: rand(), bias_o1: rand(), }; 

When we try to start a network, we get porridge.

Now we are faced with the task of “finding the most correct weights”. Why did we do this?

In the case of XOR, we know the exact logic by which this function should work, but in the case of real conditions, we almost never understand how the process that we are trying to describe works, and we only have a set of observations, our data. We teach the neural network to reproduce this “black box” that we contacted, and it usually does quite well with a sufficient number of nodes in hidden layers. Moreover, it has been mathematically proven that a single-layer network with an infinite number of neurons can "emulate" absolutely any function with infinitely large accuracy (the universal approximator theorem).

Let's go back to finding the right weights. To accomplish it, we first need to understand what we want to reduce. We need some kind of function that allows us to determine how badly we made a mistake. And when trying to change our weights - to understand whether we are moving in the right direction or not.

Two functions are most popular for these tasks: the least squares method , when the average of error squares is taken (it is convenient for regression problems, when the output is a value, for example, between 0 and 1, or 10 values ​​from -100 to 1250 - the main thing they may be in this range) and so on. LogLoss or cross-entropy , a logarithmic loss estimate that is effective for classification tasks when we try, for example, to determine which of the numbers or letters our neural network sees.

For XOR, we will use the mean of squares of errors.

 const _ = require('lodash'); var calculateError = () => _.mean(data.map(({input: [i1, i2], output: y}) => (nn(i1, i2) - y) ** 2)); 

Learning is light

It's time to learn our network.

Stepping back a bit, we should figure out how linear regression “learns”. It works as follows - we have the same MSE (mean squared error), and we are trying to reduce it. If we recall the course of mathematics, the graph of the square from X looks like this:

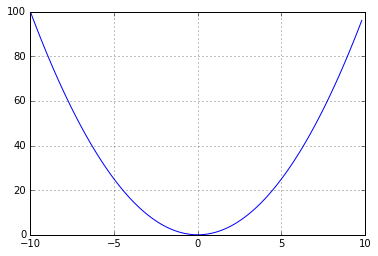
And our task is to slide to the very minimum of this parabola.

To slide to this minimum - we need to look around and understand where we have a mistake more, and where less. And then move downward. This can be done numerically (see the value for +1 and for -1 and calculate where to go), or you can mathematically by taking a derivative that characterizes the rate of change of the function. In other words, if an error increases with an increase in any parameter, the error derivative will be positive (we are on the right side of the parabola), and vice versa. We add the derivative multiplied by our weights to our own weights, and step by step we approach the answer with the smallest error until we get bored or reach a local minimum. Speaking even simpler - if we take a derivative and it is positive, then for this particular value, with an increase in the value at the input, the error will increase, and with decreasing it will decrease.

If you imagine it visually, it will look something like this:

In the comments write that initially this picture from the course Andrew Ng

If we represent our error function as (f (x) - y) * 2, then its derivative will be equal to 2 (f (x) - y) f '(x). Proof )

Since the neural network of fully connected layers (that is, the one we are talking about now) is just a chain of such linear regressions, we only need to calculate this derivative for each layer and multiply our weight coefficients on it.

Live

Probably, it's time to just show the code with an explanation of what is happening.

Embedding this amount of code in Habr is a rather cruel task, so I put the code with a large number of comments on RunKit:

https://runkit.com/jabher/neural-network-from-scratch-in-js

and in Russian:

https://runkit.com/jabher/neural-network-from-scratch-in-js---ru

and just in case - duplicate code in gist.github.com

Conclusion

Of course, neural networks are much more complex. You can, for example, see the Inception 3 scheme, which recognizes the images in the picture. In such networks, there are many tricky layers that both work and train harder than what we saw now, but the essence remains the same - multiply the matrices, calculate the error, unscrew the error in the opposite direction.

And if you want to participate in the development of a framework for neural networks, connect to us with Cazala .