MemC3 - compact Memcache with increased parallelism - due to more stupid caching and smarter hashing

This is a translation of the review of the article “MemC3: Compact and Concurrent MemCache with Dumber Caching and Smarter Hashing” by Fan et al. in Proceedings of the 10th USENIX Symposium on Networked Systems Design and Implementation (NSDI'13), pdf here

The dudes (a former googlovets, a dude from Carnegie Mellon University and another one from Intel Labs) made an improved Memcached-compatible cache (in fact they just finished memksh), and they have great performance results. I really liked the review of this article in the blog "The morning paper" - a description of the algorithms and so on.

Italics are my comments as a translator.

At the heart of MemC3, the hashing algorithm is different than the usual hash algorithm - the optimistic cuckoo hashing (cuckoo), and in addition, the special “CLOCK” algorithm of crowding out. Combined together, they give up to 30% more efficient use of memory and an increase in performance in requests per second up to 3 times compared to your usual Memcached (with loads with a predominant reading of small objects, which is typical of Facebook memoshes).
At the end of the original article there is an excellent analysis of the results obtained from the point of view of the contribution of the applied optimizations. It looks like this:

Full bandwidth (over the network) depending on the number of threads

In this analysis, we just check out the algorithms, and the details of their insertion into the memokes and testing performance techniques, please read the original article.

Maw hashing

First, let's deal with the usual cuckoo hashing. How does the most common hash table work? You hash the key and for this hash you select a table cell (bucket or bucket :) in which you want to insert or in which you can find the value corresponding to the key. Cucu hashing uses two hash functions, it turns out two possible cells to insert or search for a value.

Consider the following table, in which each row represents a cell, each of which has four slots for data. A slot is a pointer to the data itself, a key-value pair object.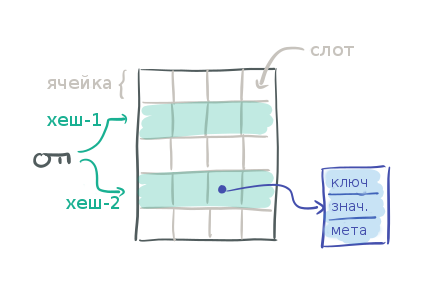

Having the key to search, we count two hashes for it and get two possible cells. That is, you need to check 2 cells × 4 slots = 8 slots to find or not to find the key you need.
That is, when searching in such a hash table, you need a lot of operations compared to the "normal" hash table.

Mapping hashing got its name because of how the insert operation is handled. First, we hash the key X , which we are going to insert using both hash functions, and we get two possible cells. If any of these cells has an empty slot, then save X there. If all the slots are occupied, then it is time for some key to move. Randomly select one slot in one of these two cells and move (or resettle) the key from it (let's call it Y ), thus freeing up space for writing X. Now we have hashed Y with two hash functions and we find the second cell where it could be, and we are trying to insert Y into it. If all the slots of this cell are also filled, then move some key from these slots to make room for Y , and continue to do so until an empty slot is found (or until we reach some maximum number of movements, for example, 500).
Here the algorithm behaves like a cuckoo - pulls out someone else's key from an already used place and puts its own one, hence the name.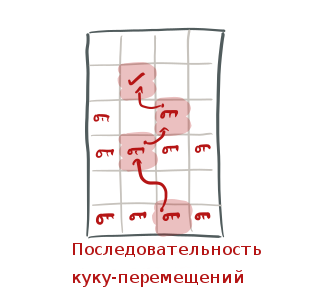

If it is not possible to find a free slot, then it is time to expand this hash table - to increase the memory allocated for it.

Although such an algorithm for insertion seems to require the execution of an entire sequence, a chain of displacements, an estimate of the time complexity of the insertion operation for cookie hashing is O (1).
Quote from the original work

Using tags to improve search operations

From the above, it is clear that there are many key samples and many comparisons, and all this is not very good from the point of view of data locality. (Apparently, the author has in mind that since neither keys, nor even key hashes are stored directly in the slots of the table cells, but are stored in separately allocated key-value structures, there are many random memory accesses and full key comparisons that allows processor caches to work well) The first thing we did to optimize cookie hashing was the introduction of tags. A tag is a 1-byte key hash value, and we will store it directly in the hash table slot next to the key pointer. Such tags allow you very quickly (just comparing one byte) to understand whether the stored key can match the desired one or not, without having to extract it by the pointer and completely compare it.

Extra extraction can occur for two different keys that have the same tag, so the key must still be extracted and compared completely to make sure that it matches the desired one. With single-byte tags, the collision rate will be only 1/2 ^ 8 = 0.39%. In the case of checking all 8 slots (for example, when searching for the missing key - miss), an average of 8 × 0.39% = 0.03 pointer dereferencing will occur. Since each cell is placed in one processor processor cache block (usually 64 bytes), on average each search will turn into only reading two blocks to check two cells plus either 0.03 pointer dereferencing if the missing key is found - miss, or 1.03 in case of a successful search - hit'e.
Quote from the original work

Using tags to improve inserts

When defining two possible cells for a key instead of using two hash functions, we will use only one hash, as well as an additional tag: let cell_1 = hash (X), and we have tag (X), then cell_2 = cell_1 ⊕ tag ( X). This construction has the following useful property - you can define cell_1, knowing the tag and cell_2. That is, in the operations of moving the key, it does not matter to us which cell the key was in, we can calculate the alternative cell without referring to the full key.

Parallel access support

Our hashing scheme, as far as we know, is the first implementation with support for parallel access (multi-reader, single writer), which has high memory efficiency (even if> 90% of the table is full).
Quote from the original work

To add parallelism to such an algorithm, you need to solve two problems:

1. avoid grandfathers when getting lock on cells for writing, because we cannot know in advance which cells will be affected by our operation
2. avoid false cache-misses, when in the process of moving some key has already been removed from one cell, but has not yet been inserted into a new one, and at that moment reading has occurred.

Of course, strictly speaking, the authors did not solve the first problem, they simply scored on it, since they allow only one write operation to be performed simultaneously. In the real world, reading often dominates the load profile, so this is a reasonable compromise.
Cache-misses (false negatives) can be avoided by first determining the full chain of cookie movements, but still not moving anything, and then performing these movements in the reverse order - from the last empty slot to the desired initial insert. Combined with the fact that write operations go in one stream, it turns out that every single exchange is guaranteed not to cause any additional movements and can be performed without the need to block the entire chain beforehand.

The most straightforward implementation is to take a lock on each of the two cells participating in the exchange (carefully with the order), and unblock them after the exchange. Here you need two locks / releases for each exchange.

We tried to optimize performance for the most common use and took advantage of having only one write thread to build all the insert'y and lookup'y in one stream of successive operations with a small overhead. Instead of locking the cells, we have a key-counter on each version. Increase the counter when moving the key when insert'e and monitor the version change during the lookup for the detection of simultaneously moving movements.
Quote from the original work

But where do you keep these counters ?? If you add them to each key-value object, then a lot of memory will be used with hundreds of millions of keys. There is also an opportunity for race-condition, since these objects are key-value, stored outside the hash table itself and, thus, are not protected by locks.

The solution is to use a fixed-size array of counters — much smaller than the number of keys. An array of 8192 counters fit into the 32KB cache, and each counter is used for several keys, due to the use of our old friend - hashing. Such a compromise, the use of such counters, still gives a good degree of parallelization of access, while maintaining the likelihood of an “extra retry” (the version counter increased by one for some other key that has a hash collision in the version counter table) low, approximately 0.01%.

These counters are inscribed in the general algorithm as follows:

• If it is necessary to move a key, the insertion process increases the version counter of this key by one to indicate the moving process in progress. After the key is moved, the counter is incremented by one again. The counting starts from zero, so the odd values ​​of the counter correspond to the locked keys, and the even numbers correspond to the unlocked keys.
• A search process that sees an odd value at the counter waits and then retries. If the counter was even, then you need to remember this value, read both cells, and then compare the value of the counter with the memorized one. If the counter value has changed, then you need to repeat the operation again.

An additional trick to optimizing cookie hash is to parallelly search for several possible insertion paths. This increases the chances of finding an empty slot faster. According to the tests it turned out that it is optimal to check in parallel two possible ways.

The displacement of "HOURS"

So far we have been talking about inserts and searches. And although optimized cookie-hashing also uses memory very efficiently, you can still expect that at some point our cache will fill up to the limit (or almost to the limit), and then you need to worry about repression.

The usual Memcached uses the preemption policy of the most recently used keys — LRU, but it requires 18 bytes per key (two pointers and a 2-byte reference counter) to ensure safe preemption is strictly in the order of LRU. This also introduces significant synchronization overhead.

In contrast, MemC3 uses only 1 bit per key with the ability to parallelize operations. This is achieved by abandoning strict LRU in favor of the approximate LRU based on the CLOCK algorithm.

Since in our target case small objects predominate, memory usage decreases when using LRU displacement, which is close to that, which allows the cache to store significantly more records, which, in turn, improves the overall hit rate. As will be shown in section 5, such preemption control gives an increase in throughput from 3 to 10 times compared to conventional Memcached, and all this with the best hit rate.
Quote from the original work

Provide a circular bit buffer and a virtual hour hand pointing to a specific place in the buffer.

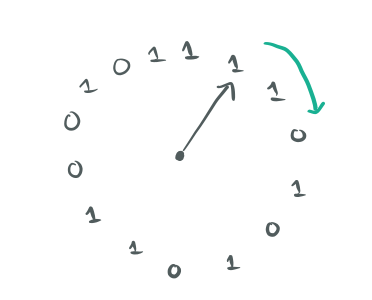
Each bit represents the "age" (age of use) of an object of a key-value pair. The bit is '1' if the corresponding key has been used recently, and '0' otherwise. Any key operation simply sets the corresponding old bit to '1'. When displacing, check the bit indicated by the clock hand. If it is '0', then you can push the corresponding key from the cache. If it is '1', then write there '0' and move the clock hand forward to the next bit. This process is repeated until a zero bit is found.

The extrusion process is integrated with an optimistic locking scheme as follows:

When the preemptive process selects the victim key X using the CLOCK algorithm, it first increments the key counter version of the X key to tell the other threads that are currently reading X that they need to try again later; then it deletes X , making it inaccessible for later reading, including for those retries from other threads; and finally increments the version counter of the X key again to complete the change cycle. Note that all pushes and inserts are serialized using locks, so that when the counters are updated they do not affect each other.
Quote from the original work

That's all. Hope you enjoyed it just like me.
Subscribe to the okmeter.io habr blog!