Functional languages in hardware design
 Functional languages, as a rule, are not very suitable for low-level programming, although they are used for code generation.
Functional languages, as a rule, are not very suitable for low-level programming, although they are used for code generation.Project examples
generation of safe C code (used in Kaspersky Lab) Ivory , support for reactive programming on Arduino , and so on Atom , Ion
But if you go down even lower, to the hardware level, then suddenly the OP is very useful. After all, a block of combinatorial logic is nothing but a function of the values of the incoming signals to the outgoing ones, and for consistent logic it is enough to add the old and the new state to the parameters and the result.
When I first learned Haskell, I joined a stormy discussion on “what is the best way to simulate an RS-trigger”. I immediately noticed that the language I’ve recently studied solves all the problems that come up in this discussion.
Modeling involves observing the evolution of a model’s state over time, but in Haskell there is no variable state as such. For that is, lazy lists that turn into "horizontal time."
')
What time?
This ridiculous term was coined by one of the participants, who was very surprised that it was more convenient for me to put the entire evolution of one signal in a line, and the next line - the whole evolution of another signal (although on large models such a format will lead to serious memory overhead and better make an effort to print the result as in ordinary languages - data output is the most difficult in Haskell). In other matters, he even liked this format, since it is more like signals on an oscilloscope, compared to printing the values of all signals in one line for each measure.
A simple way to model signals is to present them with lists of values at each moment in time. If one signal is equal to another with an offset one quantum in time, we simply add 0 to the beginning of the list:
delay s = 0:s Or so
delay = 0: You can create your own type for signals - it is more efficient, safer and more correct, but for simplicity, we still limit ourselves to using simple lists.
data Signal v = S v (Signal v) delay vs = S vs If accurate modeling of the operating time is required, the signal can be represented by a list of pairs (time interval, signal value) and provide a representation of unsteady values.
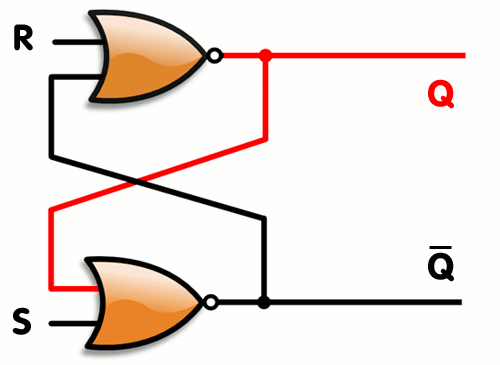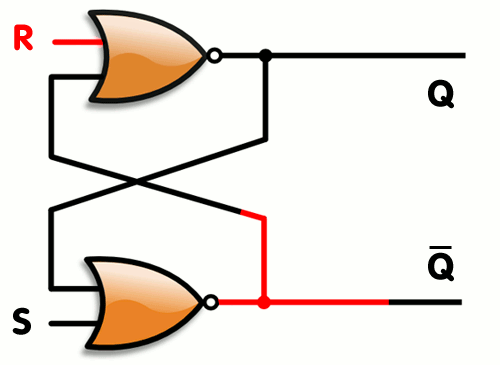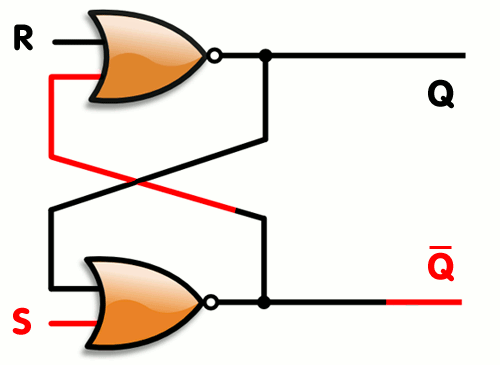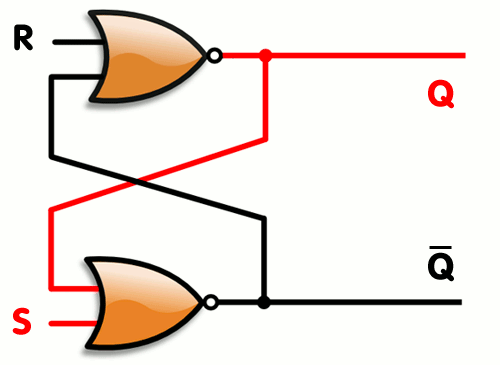
An RS trigger is a two NOR nodes interconnected mutually recursively. This system has two stable states in which the output of one NOR is one, and the other is zero. By feeding the unit to the second input of one of the NOR nodes, you can switch states.
Generally speaking, an RS trigger is an asynchronous circuit. But for the sake of simplicity, we will simulate it as synchronous, which is not quite right (even choosing the short size of “tact” is difficult to simulate transients, it is better to use a different signal representation).
nor '_' '_' = '~' nor _ _ = '_' rs rs = (q, nq) where q = '_' : zipWith nor r nq nq = '_' : zipWith nor qs main = let r = "~_______" s = "___~~___" (q,nq) = rs rs in do print r print s print q print nq Haskell Quick Reference
Names of variables (more precisely, constants, since they cannot change in the scope) and functions begin with a small letter and consist of alphanumeric characters or consist of special characters and do not begin with ':'.
Type names, constructors (we can assume that these are the names of constants in enumerations) and module names begin with a capital letter (or with a ':').
(:) - list constructor. Creates a new list by adding one element to the old one.
Strings in Haskell are represented as a list of characters. "1234" means the same as ['1', '2', '3', '4']
zip - turns two lists into pairs.
zipWith applies a function to two list items
zip is expressed through zipWith
zip3 and zipWith3 work in the same way, but for three lists.
scanl applies a function to each accumulated list item. Its type (signature) is described as:
The first argument scanl is a function of two arguments, the second is the initial value of the accumulator, the third is the input list.
($) - postfix notation for applying a function to an argument.
Often used to write fewer brackets:
fx $ gy is equivalent to fx (gy)
Writing \ xy -> fyx means an anonymous function (also called a closure) with parameters x and y.
Next meet a few obscure terms. I hope they do not scare the reader. Even if this description is too complicated, by examples it will be easy to figure out how these functions are used.
fmap - “raises” a function from a single value to a function over an entire container. The container should be a functor, but almost everything is. In particular, such containers are signals that store values for each point in time. Also such containers are lists, although for them, for historical reasons, there is a special function “map” with the same functionality.
liftA is the same as fmap, but for applicative functors (as indicated by the letter 'A' in the name). Signals are also applicative functors, and lists are more complicated. Formally, lists are also applicative functors and liftA works with them as expected. But liftA2 and liftA3 behave unexpectedly, but this is a topic for a separate article.
liftA2 and liftA3 "raise" functions from two and three arguments to functions from containers. They will work with signals, and for lists it is better to use zipWith and zipWith3.
Type names, constructors (we can assume that these are the names of constants in enumerations) and module names begin with a capital letter (or with a ':').
(:) - list constructor. Creates a new list by adding one element to the old one.
0 : [1,2,3,4,5] equivalent to [0,1,2,3,4,5]Strings in Haskell are represented as a list of characters. "1234" means the same as ['1', '2', '3', '4']
zip - turns two lists into pairs.
zip [1,2,3,4] "1234" is equal to [(1,'1'),(2,'2'),(3,'3'),(4,'4')] zipWith applies a function to two list items
zipWith (+) [1,2,3,4] [1,3,5,7] calculate the element-by-element sum of the lists [2,5,8,11]zip is expressed through zipWith
zip = zipWith (,) zip3 and zipWith3 work in the same way, but for three lists.
scanl applies a function to each accumulated list item. Its type (signature) is described as:
scanl :: (b -> a -> b) -> b -> [a] -> [b] The first argument scanl is a function of two arguments, the second is the initial value of the accumulator, the third is the input list.
scanl (+) 0 [1,2,3,4] will calculate the list of partial sums: [0,1,3,6,10]($) - postfix notation for applying a function to an argument.
f $ x = fx Often used to write fewer brackets:
fx $ gy is equivalent to fx (gy)
Writing \ xy -> fyx means an anonymous function (also called a closure) with parameters x and y.
Next meet a few obscure terms. I hope they do not scare the reader. Even if this description is too complicated, by examples it will be easy to figure out how these functions are used.
fmap - “raises” a function from a single value to a function over an entire container. The container should be a functor, but almost everything is. In particular, such containers are signals that store values for each point in time. Also such containers are lists, although for them, for historical reasons, there is a special function “map” with the same functionality.
liftA is the same as fmap, but for applicative functors (as indicated by the letter 'A' in the name). Signals are also applicative functors, and lists are more complicated. Formally, lists are also applicative functors and liftA works with them as expected. But liftA2 and liftA3 behave unexpectedly, but this is a topic for a separate article.
liftA2 and liftA3 "raise" functions from two and three arguments to functions from containers. They will work with signals, and for lists it is better to use zipWith and zipWith3.
This approach makes it relatively easy to model quite complex circuits at the RTL level. The clock signal is clearly not present, but is implied wherever it is needed. Registers can be modeled using a delay or by explicitly providing for the state in the parameters and the return value of the node code.
macD rxy = acc where prods = zipWith (*) xy sums = zipWith (+) acc prods acc = 0 : zipWith (\rv -> if r == 1 then 0 else v) r sums macS rxy = scanl macA 0 $ zip3 rxy where macA acc (r,x,y) = if r == 1 then 0 else acc+x*y Two equivalent models of MAC operation (multiplication with addition) with a battery are described here. macD - using a recursive signal with a delay, macS - using an explicitly described state.
If a Haskell subset simulates synchronous hardware so well, then why not synthesize HDL from it? There are several compiler extension projects that allow you to do this: commercial Bluespec , free Lava and CλaSH .
Clash
As an example, I want to consider Clash, since it can compile both in VHDL, in SystemVerilog, and in good old Verilog (which attracts me because it is used not only in microelectronics :)
The installation process is described in sufficient detail on the site. You should pay attention to it - firstly, compatibility with ghc-7.x is declared (that is, it may not work with 8.x), secondly you do not need to try to run “cabal install clash” - this is an outdated package, you need to install clash-ghc ( "Cabal install clash-ghc --enable-documentation").
The clash executable (or clash.exe, depending on the OS) will be installed in the "~ / .cabal / bin" directory, it is better to add it to $ PATH.
The main node from which the clash starts compiling is called topEntity, which is a function from the incoming signal to the outgoing signal (of course, the signals can be composite).
For example, consider a one-bit adder:
topEntity :: Signal (Bool, Bool) -> Signal (Bool, Bool) topEntity s = fmap (\(s1,s2) -> (s1 .&. s2, s1 `xor` s2)) s Whole file
module ADD1 where import CLaSH.Prelude topEntity :: Signal (Bool, Bool) -> Signal (Bool, Bool) topEntity = fmap (\(s1,s2) -> (s1 .&. s2, s1 `xor` s2)) fmap turns a function of a pair of logical quantities into a function of a signal. You can compile the file in verilog using the command "clash --verilog ADD1.hs"
Result
// Automatically generated Verilog-2001 module ADD1_topEntity_0(a1 ,result); input [1:0] a1; output [1:0] result; wire [0:0] app_arg; wire [0:0] case_alt; wire [0:0] app_arg_0; wire [1:0] case_alt_0; wire [0:0] s1; wire [0:0] s2; assign app_arg = s1 & s2; reg [0:0] case_alt_reg; always @(*) begin if(s2) case_alt_reg = 1'b0; else case_alt_reg = 1'b1; end assign case_alt = case_alt_reg; reg [0:0] app_arg_0_reg; always @(*) begin if(s1) app_arg_0_reg = case_alt; else app_arg_0_reg = s2; end assign app_arg_0 = app_arg_0_reg; assign case_alt_0 = {app_arg ,app_arg_0}; assign s1 = a1[1:1]; assign s2 = a1[0:0]; assign result = case_alt_0; endmodule To work with the state, you can use the Moore and Miles machines. Consider a frequency divider, first with the help of Moore’s automaton.
data DIV3S = S0 | S1 | S2 div3st S0 _ = S1 div3st S1 _ = S2 div3st S2 _ = S0 div3out S2 = True div3out _ = False topEntity :: Signal Bool -> Signal Bool topEntity = moore div3st div3out S0 data is a Haskell construct that describes a data type. In this program, we describe the type of DIV3S representing the state of our automaton. Possible values of this type are listed in '|' - S0, S1 and S3.
div3st is a state function (it is customary to call the unused parameter by the "_" symbol, in this case, the value of the input signal).
div3out is a function from state to value of the output signal.
The library function moore creates a node based on these two functions and the initial state.
Output systemverilog
// Automatically generated SystemVerilog-2005 module DIV3Moore_moore(w3 ,// clock system1000 ,// asynchronous reset: active low system1000_rstn ,result); input logic [0:0] w3; input logic system1000; input logic system1000_rstn; output logic [0:0] result; logic [1:0] s1_app_arg; logic [1:0] s1; always_comb begin case(s1) 2'b00 : s1_app_arg = 2'd1; 2'b01 : s1_app_arg = 2'd2; default : s1_app_arg = 2'd0; endcase end // register begin logic [1:0] dout; always_ff @(posedge system1000 or negedge system1000_rstn) begin : DIV3Moore_moore_register if (~ system1000_rstn) begin dout <= 2'd0; end else begin dout <= s1_app_arg; end end assign s1 = dout; // register end always_comb begin case(s1) 2'b10 : result = 1'b1; default : result = 1'b0; endcase end endmodule The same with the Miles machine:
data DIV3S = S0 | S1 | S2 div3 S0 _ = (S1, False) div3 S1 _ = (S2, False) div3 S2 _ = (S0, True) topEntity :: Signal Bool -> Signal Bool topEntity = mealy div3 S0 Output VHDL
-- Automatically generated VHDL-93 library IEEE; use IEEE.STD_LOGIC_1164.ALL; use IEEE.NUMERIC_STD.ALL; use IEEE.MATH_REAL.ALL; use std.textio.all; use work.all; use work.div3mealy_types.all; entity div3mealy_mealy is port(w2 : in boolean; -- clock system1000 : in std_logic; -- asynchronous reset: active low system1000_rstn : in std_logic; result : out boolean); end; architecture structural of div3mealy_mealy is signal y : boolean; signal result_0 : div3mealy_types.tup2; signal x : unsigned(1 downto 0); signal x_app_arg : unsigned(1 downto 0); signal x_0 : unsigned(1 downto 0); begin result <= y; y <= result_0.tup2_sel1; with (x) select result_0 <= (tup2_sel0 => to_unsigned(1 ,2) ,tup2_sel1 => false) when "00", (tup2_sel0 => to_unsigned(2,2) ,tup2_sel1 => false) when "01", (tup2_sel0 => to_unsigned(0,2) ,tup2_sel1 => true) when others; -- register begin div3mealy_mealy_register : process(system1000,system1000_rstn) begin if system1000_rstn = '0' then x <= to_unsigned(0,2); elsif rising_edge(system1000) then x <= x_app_arg; end if; end process; -- register end x_app_arg <= x_0; x_0 <= result_0.tup2_sel0; end; In Clash, instead of lists, vectors of fixed size are used and most of the library functions are redefined to work with them. You can get to the standard list functions by adding to the file (or by running in the REPL) the line
import qualified Data.List as L After that, you can use functions by explicitly specifying the “L.” prefix. for example *DIV3Mealy L> L.scanl (+) 0 [1,2,3,4] [0,1,3,6,10] Most of the usual list functions work with vectors.
*DIV3Mealy L> scanl (+) 0 (1 :> 2 :> 3 :> 4 :> Nil) <0,1,3,6,10> *DIV3Mealy L> scanl (+) 0 $(v [1,2,3,4]) <0,1,3,6,10> But there are many subtleties, for details, refer to the documentation .
A guide with examples can be found here .
The site has examples of projects on Clash, in particular the implementation of the processor 6502 .
Perspectives
Haskell is a very powerful language, and it is possible to use it to develop DSL, for example, to develop a device’s software interface (with generation, in addition to HDL, also via Ivory drivers and emulators for virtualization systems), or architecture and microarchitecture (with generation of LLVM backend, optimizing for this microarchitecture).
Taking this opportunity, I express my gratitude to yuripanchul for organizing the publication of the textbook “Digital Circuit Design and Computer Architecture”, which I am currently reading, and which encouraged me to write this article.
Source: https://habr.com/ru/post/316748/
All Articles