HV or How to draw binary trees nicely
Somehow I wanted to write something for a long time, but it all happened. And then the case presented itself, and even more so the Internet did not immediately give anything ...
I would like to say a big thank you to A. Dainyak for the course you have read and add that this is just a presentation of a piece of the course, and I don’t pretend to be more.
Everywhere in the article tree = binary tree
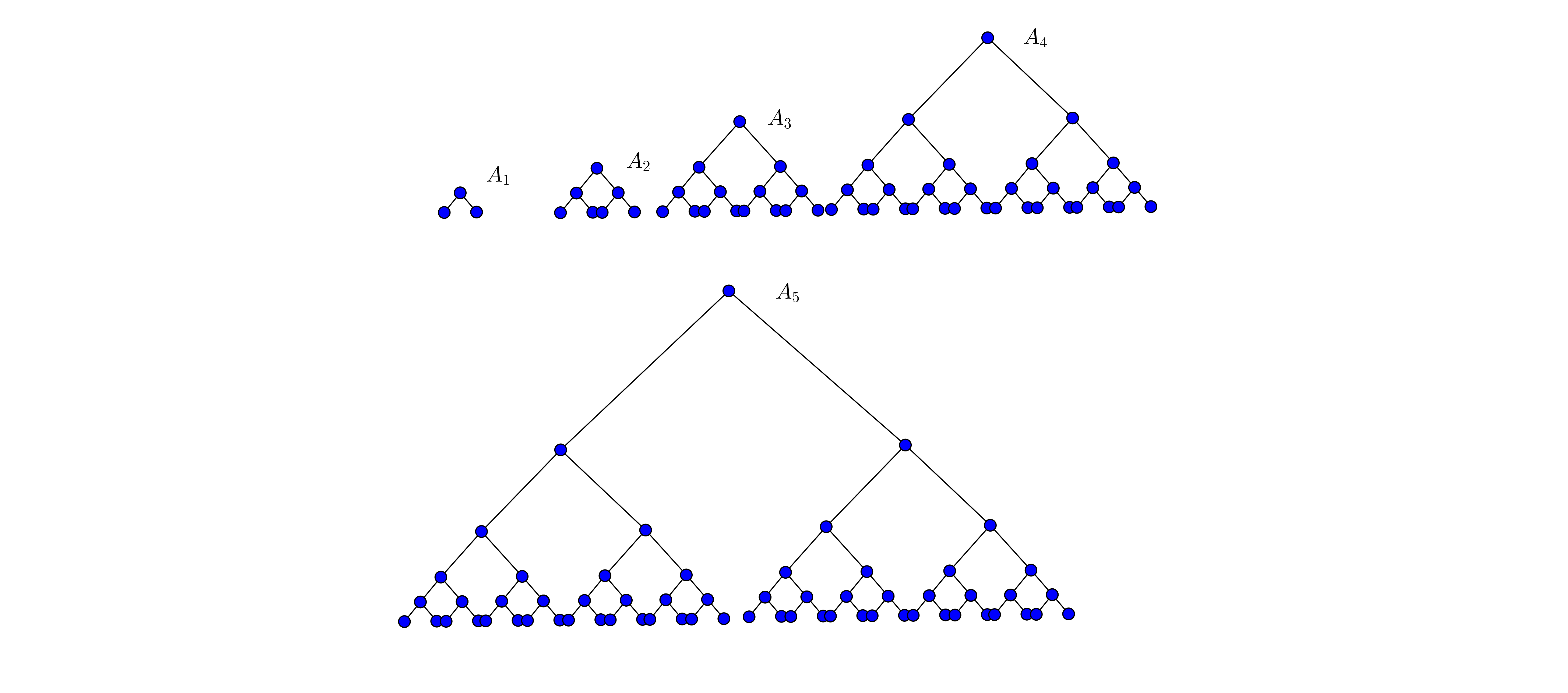
Indeed it is not difficult to draw small trees (eg 5-10) sheets. And for them, you can use the natural representation (which is the type of LPC) . And it works pretty well.
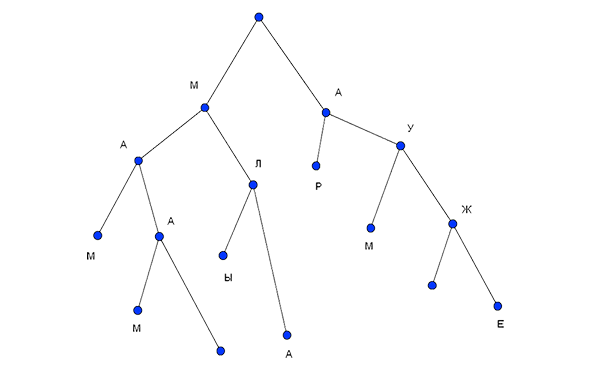
Maybe you can even try to draw a tree of 100 nodes. But if there are more nodes - for example, 1000, then you can draw trees. But to read them (and understand) will be quite inconvenient. Moreover, by reading we understand precisely the image of a tree on the screen, such that they simply do not smear infinitely strong, i.e. into one big spot.
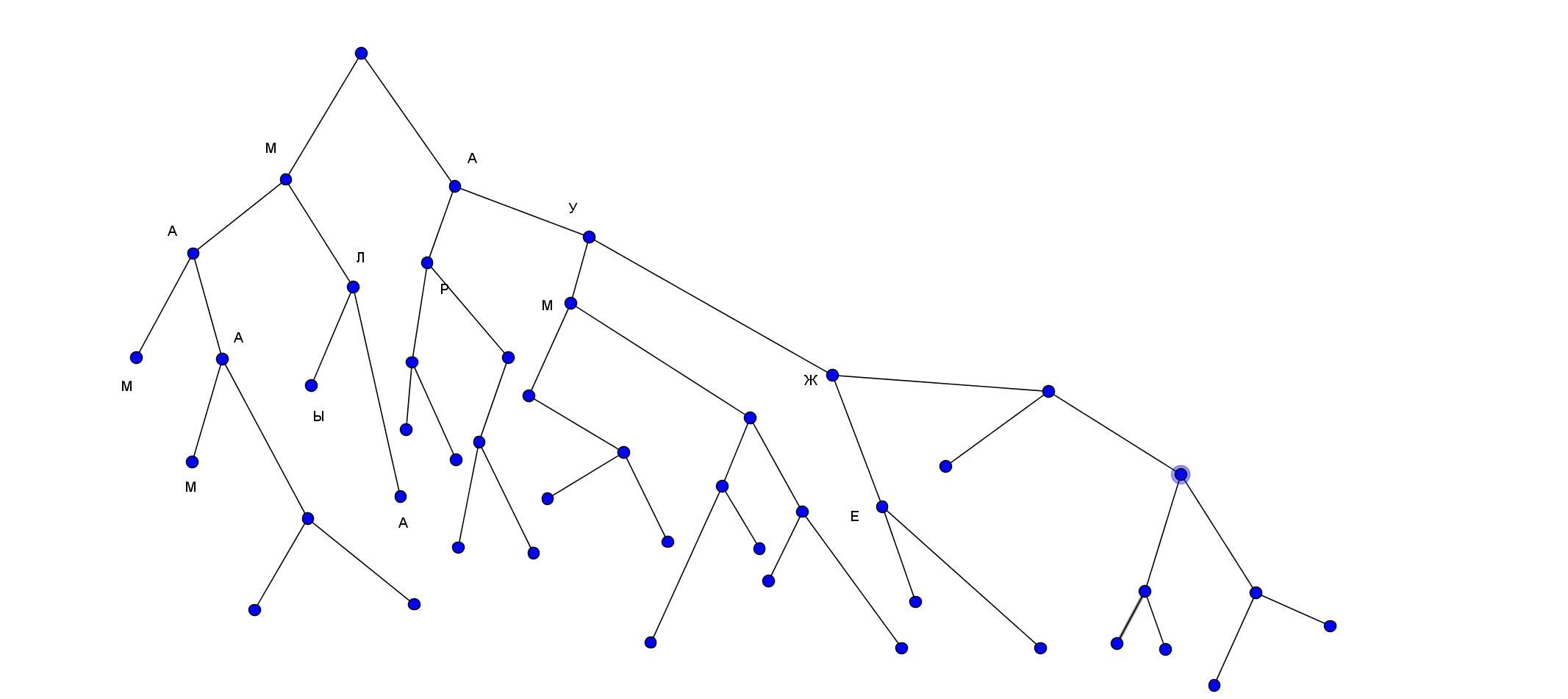
One of the options for dealing with this, but probably not even how much of a struggle, but simply some kind of normal visualization structure - H orisontal V ertical- tree. That is, the following is used for visualization:
')
So, the concept of the HV-tree view is simple (and recursive): if we have tree 1 and tree 2 and we want to combine them (that is, to make subtrees of the same tree, then this is how the operation will be done:
That is, how the gluing takes place quite formally:
1. We have a given edge length (which is, in general, natural). And we can glue in what rule. What are we doing:
Stand at the root, S = 0. We go from the root to all sheets and every time we go to the right (from the screen) S = S + 1.
2. The same with the second tree.
3. Down we fix the tree, which is wider (in which S is larger). And to the right - the rest.
If they are equal, it doesn’t matter how we hang (although of course we’d rather have a long down, if we still want to somehow limit the drawing, but if we are not limited in our view, it’s worth trying the other way around, it’s more convenient to see).
That's exactly how we define these trees and the process and construction.
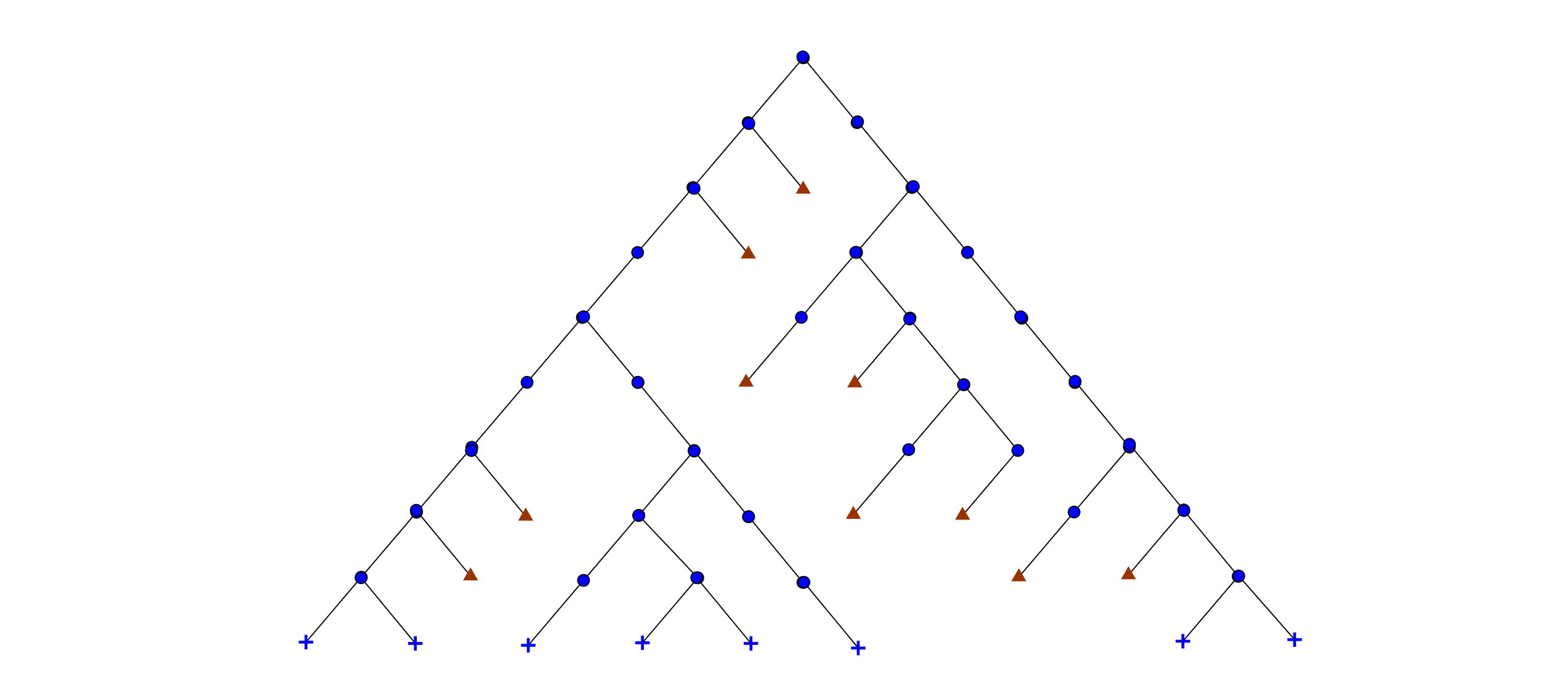
Well, as an example - a comparison of the presentation in std form and HW-packing.
Here it is. Such a representation, which in principle reads slightly better than the standard representation.
I would like to say a big thank you to A. Dainyak for the course you have read and add that this is just a presentation of a piece of the course, and I don’t pretend to be more.
Everywhere in the article tree = binary tree
Indeed it is not difficult to draw small trees (eg 5-10) sheets. And for them, you can use the natural representation (which is the type of LPC) . And it works pretty well.

Maybe you can even try to draw a tree of 100 nodes. But if there are more nodes - for example, 1000, then you can draw trees. But to read them (and understand) will be quite inconvenient. Moreover, by reading we understand precisely the image of a tree on the screen, such that they simply do not smear infinitely strong, i.e. into one big spot.

One of the options for dealing with this, but probably not even how much of a struggle, but simply some kind of normal visualization structure - H orisontal V ertical- tree. That is, the following is used for visualization:
')
- We walk only in
 . Although it is not necessary from the point of view of implementation. Just so it will be convenient for us.
. Although it is not necessary from the point of view of implementation. Just so it will be convenient for us. - We would like us to somehow successfully win in the area and readability. (But now I don’t want to talk about it, it can only be said that the super-long and long strip-tree is completely unreadable.)
So, the concept of the HV-tree view is simple (and recursive): if we have tree 1 and tree 2 and we want to combine them (that is, to make subtrees of the same tree, then this is how the operation will be done:
That is, how the gluing takes place quite formally:
1. We have a given edge length (which is, in general, natural). And we can glue in what rule. What are we doing:
Stand at the root, S = 0. We go from the root to all sheets and every time we go to the right (from the screen) S = S + 1.
2. The same with the second tree.
3. Down we fix the tree, which is wider (in which S is larger). And to the right - the rest.
If they are equal, it doesn’t matter how we hang (although of course we’d rather have a long down, if we still want to somehow limit the drawing, but if we are not limited in our view, it’s worth trying the other way around, it’s more convenient to see).
That's exactly how we define these trees and the process and construction.
Well, as an example - a comparison of the presentation in std form and HW-packing.
- Incomplete tree in std. submission.
- Full tree in std. representation: I must say that we can not imagine the whole tree with edges of the same width. (Or rather, if the edge comes from a node at the bottom n level (the sheet is level 0, the prelist is 1), then the edge length should be n * s, where s is the unit edge. (In my drawing this is not right, therefore that I moved the corners of the ribs.)
- The first tree in the HV-representation. This is the same tree as in the first picture.
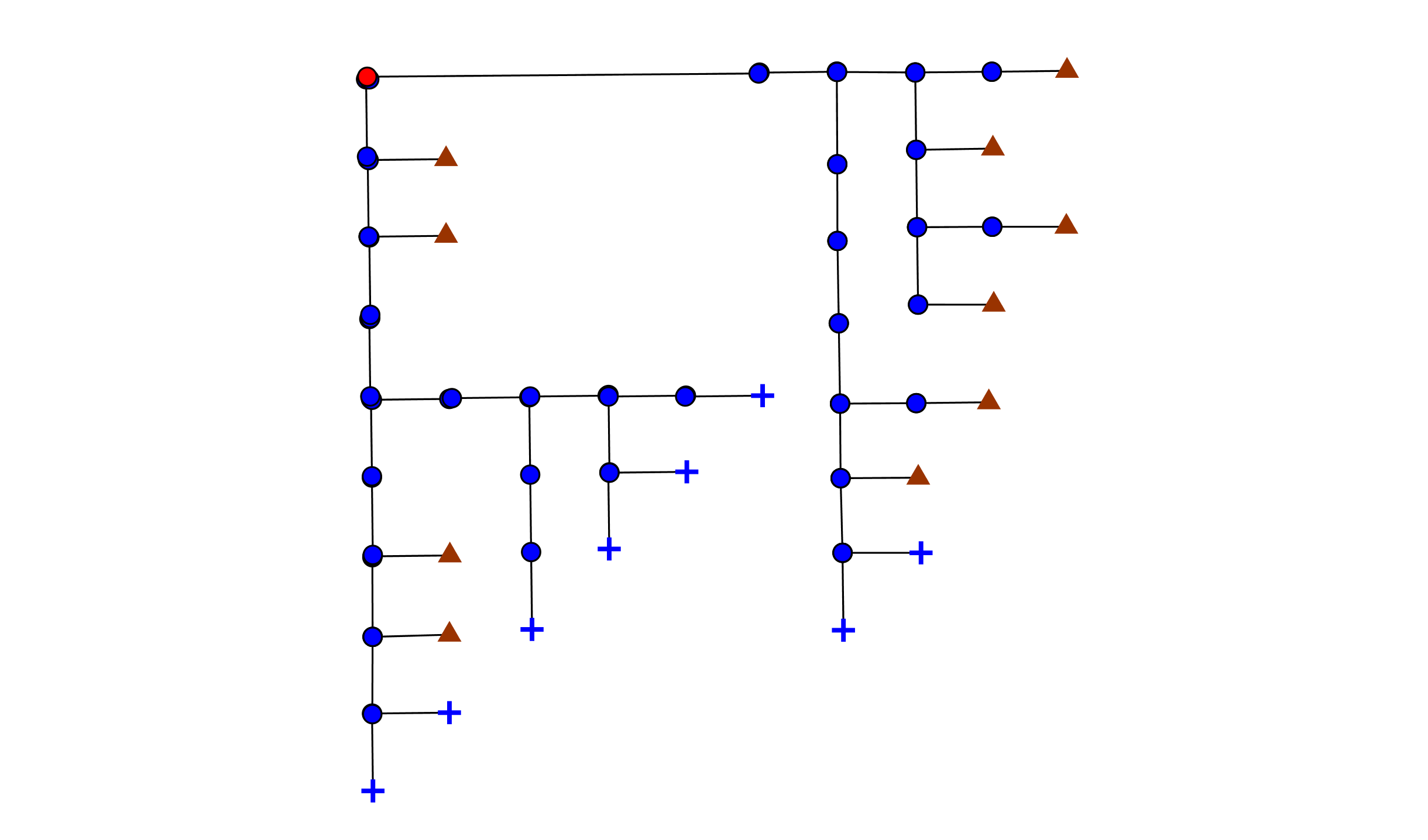
Here it is. Such a representation, which in principle reads slightly better than the standard representation.
Source: https://habr.com/ru/post/315718/
All Articles