How to solve simple optimization problems on python using cvxpy
Good day to all! With a simple search, I was unable to detect the mention of the cvxpy module , and therefore I decided to write training material on it - just code examples that make it easier for a beginner to use this module for their tasks later. cvxpy is designed to solve optimization problems - finding the minima / maxima of functions under certain constraints. If you are interested in this topic - please under the cat.

Here x is an independent variable (generally a vector), f (x)
target function to be optimized. Restrictions on the domain of f (x) can be specified using equalities and inequalities.
Let's consider the following linear programming problem:
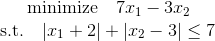
')
If you look at the region defined by the inequality with the module, you can see that this region can easily be defined using linear inequalities:

In our case, the restrictions will be as follows:

The module installation is described in detail on the module website . Let's write a simple code that will allow us to solve our test optimization problem:
Our current solution is not integral and goes beyond the limits, however, it can be seen that it lies near the optimal solution (-9, 3) . In cvxpy, you can use different solvers to solve a problem, selecting the best one. Let's try GLPK :
The list of available solvers is returned by the
You can solve not only linear programming problems. Let's look at the original wording of the problem:
You can also search for a solution for the method of least squares :
Of course, some tasks may have a trivial solution:
And some may not have a solution at all:
That's all. You can learn more on the module website .
General formulation of the problem

Here x is an independent variable (generally a vector), f (x)
target function to be optimized. Restrictions on the domain of f (x) can be specified using equalities and inequalities.
Example task
Let's consider the following linear programming problem:
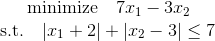
')
If you look at the region defined by the inequality with the module, you can see that this region can easily be defined using linear inequalities:

In our case, the restrictions will be as follows:

Solving a problem with cvxpy
The module installation is described in detail on the module website . Let's write a simple code that will allow us to solve our test optimization problem:
import numpy as np import cvxpy as cvx # x = cvx.Variable(2) A = np.array([[1, 1], [1, -1], [-1, 1], [-1, -1]]) b = np.array([8, 2, 12, 6]) c = np.array([7, -3]) # constraints = [A * x <= b] # obj = cvx.Minimize(c * x) # prob = cvx.Problem(obj, constraints) prob.solve() print(prob.status) # optimal print(prob.value) # -71.999999805 print(x.value) # [[-8.99999997] [ 3.00000002]] Our current solution is not integral and goes beyond the limits, however, it can be seen that it lies near the optimal solution (-9, 3) . In cvxpy, you can use different solvers to solve a problem, selecting the best one. Let's try GLPK :
prob.solve(solver = "GLPK") print(prob.status) # optimal print(prob.value) # -72.0 print(x.value) # [[-9.] [ 3.]] The list of available solvers is returned by the
installed_solvers() function.Other examples
You can solve not only linear programming problems. Let's look at the original wording of the problem:
# constraints = [cvx.abs(x[0] + 2) + cvx.abs(x[1] - 3) <= 7] # obj = cvx.Minimize(c * x) # prob = cvx.Problem(obj, constraints) prob.solve(solver = "GLPK") print(prob.status) # optimal print(prob.value) # -72.0 print(x.value) # [[-9.] [ 3.]] You can also search for a solution for the method of least squares :
# obj = cvx.Minimize(cvx.norm(A * x - b)) # # prob = cvx.Problem(obj) prob.solve() print(prob.status) # optimal print(prob.value) # 13.9999999869 print(x.value) # [[-2.] [ 3.]] Of course, some tasks may have a trivial solution:
A = np.array([[1, 1], [1, -1], [-1, 1]]) b = np.array([8, 2, 12]) c = np.array([7, -3]) # constraints = [A * x <= b] # obj = cvx.Minimize(c * x) # prob = cvx.Problem(obj, constraints) prob.solve() print(prob.status) # unbounded print(prob.value) # -inf print(x.value) # None And some may not have a solution at all:
A = np.array([[1, 1], [1, -1], [-1, 1], [-1, -1]]) b = np.array([-6, -12, -2, -8]) # constraints = [A * x <= b] # obj = cvx.Minimize(c * x) # prob = cvx.Problem(obj, constraints) prob.solve() print(prob.status) # infeasible print(prob.value) # inf print(x.value) # None That's all. You can learn more on the module website .
Source: https://habr.com/ru/post/315236/
All Articles