VaR as a way to assess risk. Historical method

In this article I want to introduce you to the popular VaR ( ValueAtRisk ) financial risk assessment tool . In this case, I will try to use a minimum of economic, mathematical and statistical terms.

The main VaR ideas were developed and applied at JP Morgan in the 80s. VaR was widely applied in 1993 when it was approved by the Group of Thirty (G-30) as part of the “best practices” for working with derivatives (derivative financial instruments). And later it became one of the bank’s risk indicators for the Basel II system (a set of international recommendations on banking regulation). The idea used in VaR can be traced back to the early works of Nobel Prize winner in economics, Garia Markowitz in 1952.

Why do you need VaR?

VaR has many uses:
')

• banks determine the current risk by department and bank in general;
• traders use VaR in their trading strategies (for example, to determine when to exit a trade);
• private investors to choose less risky investments;

Management of risks

First, let's understand what risk management is and why it is needed.

“Risk management is the process of detecting, analyzing and making or mitigating uncertainty in investment decisions. In essence, risk management always happens when an investor or a fund manager analyzes and tries to assess potential losses and then take (or not take) the necessary measures, given his investment objectives and risk tolerance. ”

→ Source

Why is risk management relevant? Daniel Kaneman, in his book “ Think slowly ... decide quickly ”, says that people do not like to lose more than they like to win. That is, if a person is offered to win $ 50 with 50% and lose $ 100 from 50%, he will most likely refuse, although the potential gain is even greater. The author calls this loss asymmetry.

Predicting possible losses to which people are so sensitive, we will deal with you. But before moving on to VaR, we need to talk about the concept of volatility , without which it is impossible to imagine risk management .

Little about volatility

First, consider two examples.

Example 1 - let the whole of last year's action A every day either grow by 3% or lose -1%. At the same time, these two events were independent and equally probable. If our investments are $ 100, then we can with high probability say that the trend will continue tomorrow and we will either receive $ 3 or lose $ -1 with the same probability. In other words, the probability of getting + 3 $ is 50% and the probability of losing $ -1 is also 50%. We can even say that the expected profit every day is $ 1 ($ 3 * 50% -1 $ * 50%). But as we will see later, the expected profit is not what interests us in risk management. Losses are important for us, and with possible losses everything is clear here - with a probability of 50%, we can lose $ 1 .


Random income + 3% or -1%

Now let's look at example 2 . There is information about the daily income of share B in the past year. Income properties:

• took one of four values ​​-4%, -3%, + 5%, + 6%;
• the probability of each of the four events is the same - 25%;

Random income -3%, -4%, 5% or 6%

I specially selected the values ​​so that the average value was +1% (- 4% * 25% -3% * 25% + 5% * 25% + 6% * 25%) as in the first example. That is, if we have shares for $ 100, then the expected value tomorrow will also be $ 1 .


Comparison of example 1 (-1%, + 3%) and example 2 (-3%, -4%, 5%, 6%)

Although the expected values ​​are the same in two cases (+ 1%), the level of risk is different, since the amount of losses may be higher in the second case. This is volatility .

Volatility, volatility (English volatility) - a statistical financial indicator characterizing price volatility. It is the most important financial indicator and concept in financial risk management, where it is a measure of the risk of using a financial instrument for a given period of time.

Or in your own words, volatility is the strength of the spread of values. The greater the spread, the higher the volatility and the harder it is for us to make a price assumption in the future. The conclusion is: the higher the volatility, the higher the risk . It would seem that volatility is the indicator that we need.

But volatility has one major drawback for risk management. It takes into account both the spread of profits and the spread of losses. For example, if the share price rises sharply, then volatility will increase. Although the risk, in terms of possible losses, will remain at the same level. This problem will be solved by VaR, but before moving on to VaR, let's deal with the problem of estimating losses.

Problem 1 . How to describe potential losses?

If in the first example the loss forecast for tomorrow was -1% with a probability of 50% , then in the second example the situation is more complicated. We can say that:

• with a probability of 25%, we will lose 3%;
• with a probability of 25%, we will lose 4%;
• With a probability of 50%, we will lose more than 3%;

All these statements are true, and in fact we have only 4 possible outcomes . In real life, the number of outcomes can be much greater. Accordingly, the number of statements we can make about the probability of risk will increase. This complicates the reporting and analysis of information.

Problem 2. Extreme values.

Let's imagine that last year the stock took values ​​from -5% to 5%, but in one day the loss was -10%. If we take the number of days in a year for 364 (for simplicity, let's forget about weekends and holidays), then the probability of a repeat loss of -10% is 1/364 = 0.274%. The probability of 0.274% is quite small, it is difficult to imagine, and someone may consider it not at all essential for consideration. How to be in this case?

In both of these cases, VaR comes to our rescue.

VaR

VaR allows you to estimate losses with a certain probability. And this can be done quite briefly so that a person can relatively easily imagine the size of the risk. VaR answers the following question:

“ What is the maximum loss I can expect for a certain period of time with a given level of probability (confidence)”

For example, VaR $ 100 with a threshold of 99% means:

• with a probability of 1%, we can lose $ 100 or more during the day;
• with a probability of 99%, we will not lose more than $ 100 during the day;

Both of these statements are equivalent.

VaR consists of three components:

• forecast level / threshold (usually 95% or 99%);
• time interval of the forecast (day, month or year);
• possible losses (the amount of money (usually dollars) or interest);

The ability to choose a threshold (99% in our example) is a very convenient feature for many investors. This property allows you to approach the answer to the question that many investors care about “ how much can we lose during the day (month) in the worst case? ".

There are three methods for obtaining VaR: historical , covariance, and the Monte Carlo method .

In this article we will look at the historical method , since it requires the least knowledge of statistics and, in my opinion, the most intuitive of the three.

VaR Counting Steps:

1. Collect historical income data for a specific period (month, year);
2. Sort data ascending;
3. Choose the threshold with which we want to make a forecast and “cut off” the worst value knowing the threshold;

For greater clarity, let's perform this process of finding VaR for a real example. As an example, we’ll look at Apple stock prices in 2015.

Steps:

1. Get data on stock returns as a percentage . You can download data for example from yahoo.finance.com. Yahoo provides opening, closing and other prices. We will consider closing prices (close *). Notice that the yahoo dates are sorted in descending order, so you can sort them in ascending order. We convert the closing prices to profit as a percentage from the previous day. For example, if the price was $ 10 yesterday, and today is $ 15, then the percentage profit will be ($ 15 -10 $) / $ 10 = 50%;

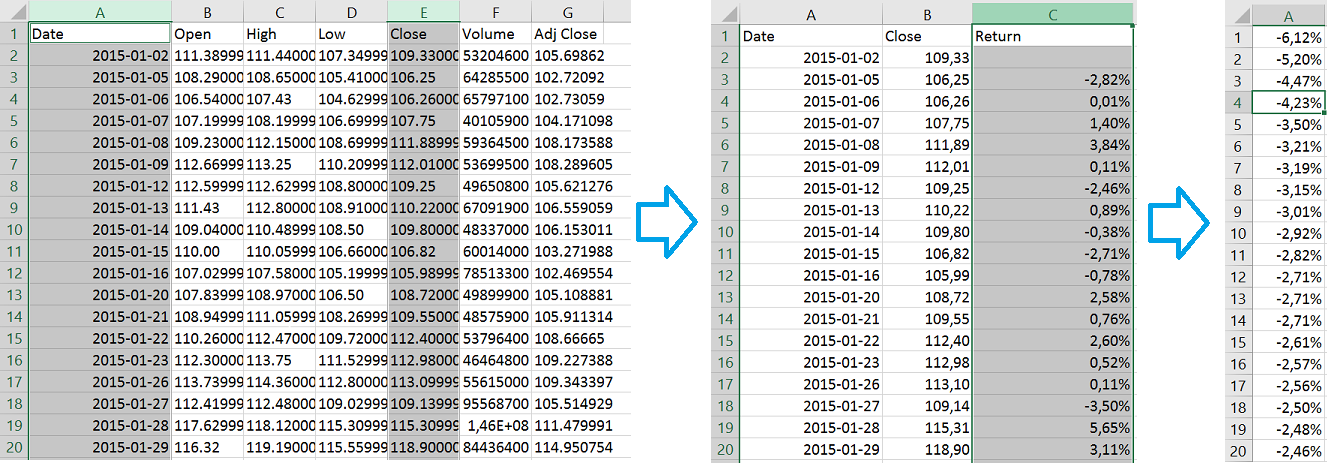Yahoo data conversion and sorting


2. Sort profits in ascending order (for clarity, I built a histogram);

3. Select the threshold with which we want to make a forecast, and “cut off” the worst value knowing the threshold. We have 252 business days. If we want to make an assessment covering 95% of cases, then we discard the worst 5%, the probability of which we consider low. 5% of 252 days is 13 days (rounded up 12.6 to 13). If you look at the chart, it is clear that the income of the 13th “worst day” was -2.71%. Now we can say that with a 95% probability we will not lose more than 2.71%. If our investment is $ 100, then with a 95% probability we will not lose more than $ 2.71. This does not mean that we can not lose more than $ 2.71 , we are talking about a probability of 95%. If this is not enough, then you can increase the threshold, for example, up to 99%;

* We choose close price, not adj. close since adj. close is variable and may change over time. For example, if split shares occur. Our goal is for the numbers to match those who follow this example later.

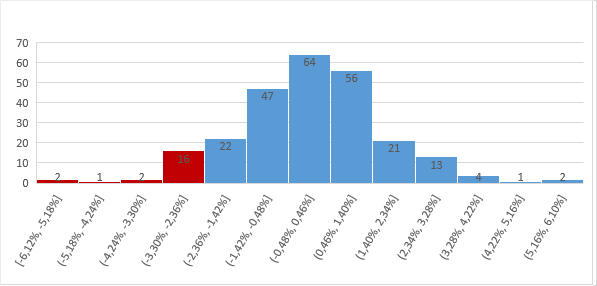Concluding the example with data from Apple, here is another interesting graph. On the chart, horizontally, we see the ranges of profits, and vertically - the number of days when the profit fell in the corresponding interval. This graph is very similar to the normal distribution . This fact will be useful to us in the following articles where we consider two other methods for calculating VaR.


A little about the shortcomings of the historical method and VaR in general:

• We predict the future using historical data. This may be a fragile assumption. As we make the assumption that events from the past will be repeated. You can try to deal with this using different time intervals to calculate VaR (year, month, day). We will discuss this below.
  
  
• VaR says nothing about values ​​outside the threshold, for example 95%. We can have two different A and B stocks with a VaR of $ 50 at a threshold of 95% and 100 observations. Let the 95 best observations of A and B are the same and equal from -50 $ to 45 $ with a step of 1 $. But the five worst profits are A = {-1000 $, -800 $, -700 $, -600 $, -500 $}, and B = {-100 $, -99 $, -98 $, -97 $, -96 $}. Obviously, the risk for B is higher. You can try to deal with this by increasing the threshold (up to 99%, 99.9%, 99.99%, etc.). There are also methods specifically designed to remedy these shortcomings, for example, Conditional VAR, which estimates losses if losses exceed VaR. But we will not consider them in this article.

Questions that may arise when working with VaR:

• How to choose a period?
• There is no definite answer to this, it all depends on your investment horizon. Banks usually consider VaR for days; pension funds, on the other hand, often consider VaR for months.
• What if 95% is not a whole item number?
• In our example, we used 252 days and a 95% threshold. The element that we cut equals 252 * 0.05 = 12.6. In our example, we just rounded and took the 13th element, but to be precise, our value should be somewhere in the middle. Unfortunately, in our example, the 12th and 13th elements are -2.71%. Therefore, let's imagine that the 12th element is -4%, and the 13th is -3%. Then VaR will be between -4% and -3%, closer to -3%. Or rather -3.6%. Here interpolation comes to our rescue. The formula looks like this:
  

  b + (ab) * k, where a is the lower value, b is the upper value, and the k-fractional part (in our case, 0.6)

  
  It turns out -3% + (-4% + 3%) * 0.6 = -3.6%

Conclusion

The beauty of the VaR approach is that it works great for a collection of several stocks or a combination of different securities. For example, VaR for a set of bonds and currencies gives us an estimate without much effort. And the use of other methods, such as analyzing possible scenarios, is greatly complicated due to the correlation (connection) between securities.

→ Source