Lock-free data structures. Iterators: multi-level array

In the previous parts of the opus ( 1 , 2 , 3 ) we looked at the internal structure of the lock-free map and made sure that all the basic operations — finding, adding and deleting a key — can be performed without global locks and even in a lock-free manner. But the standard std::map supports another very useful abstraction - iterators. Is it possible to implement an iterable lock-free map?
The answer to this question - under the cut.

A year ago, I was sure that iterators in principle are not realizable for lock-free containers. Judge for yourself: the iterator allows you to bypass all the elements of the container; but in the world of lock-free, the contents of the container are constantly changing, what should be considered as “bypassing all the elements”?



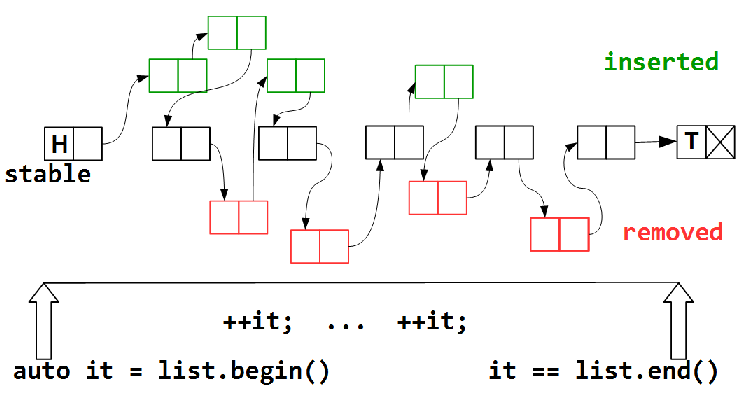
Iteration — traversing the elements of a container — takes some time, during which some elements will be removed from the container, others added, but there must be some subset of stable (possibly empty) elements that are present in the container during the entire traversal period - from list.begin() to list.end() . In addition to them, we can visit some of the added elements, like some of the deleted ones, as the map will fall. Obviously, the task to visit all the elements in the lock-free map is impossible, we cannot freeze the state of our container for the whole duration of the tour; such a freeze actually means prohibiting other threads from performing modifying operations on the container, which is tantamount to blocking.
')

So, we will consider as a bypass of a competitive container a guaranteed visit to all nodes from the stable subset.

In addition to the question "what is considered a bypass of a competitive container," there are two problems:

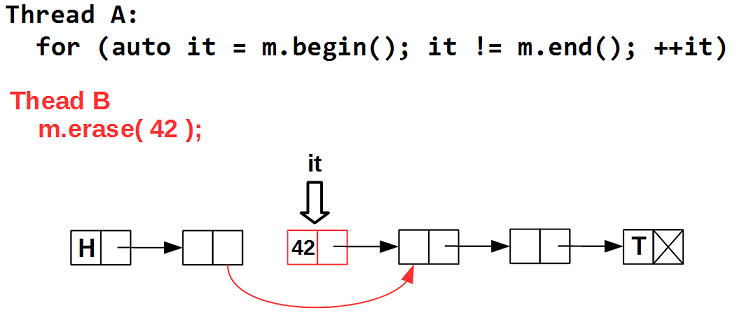
Problem 1 . An iterator is essentially a specialized pointer to a container element. Using an iterator, we access the element itself. But in a competitive container, the element on which the iterator is positioned can be deleted at any time. That is, an iterator can become invalid at any time, pointing to a deleted item, that is, to garbage:



The solution to this problem in the Hazard Pointer scheme is the hazard pointer itself. Recall that the HP schema ensures that while the pointer is declared as hazard, it (the pointer) cannot be physically removed, that is, it cannot turn into garbage. We introduce the following useful abstraction — the guarded_ptr protected pointer:

 template <typename T> struct guarded_ptr { hp_guard hp; //   T * ptr; //   guarded_ptr(std::atomic<T *>& p) { ptr = hp.protect( p ); } ~guarded_ptr() { hp.clear(); } T * operator ->() const { return ptr; } explicit operator bool() const { return ptr != nullptr; } }; 

As you can see, guarded_ptr is just a pointer with a hazard pointer. Hazard pointer hp protects the pointer to the ptr element, preventing its physical removal. Now, even if a stream B deletes the element to which the iterator is positioned, this element will be excluded from the container, but not physically deleted until the iterator's hazard pointer contains a link to this element.

Thus, in the HP schema, the iterator class will look like this:

 template <typename T> class iterator { guarded_ptr<T> gp; public: T* operator ->() { return gp.ptr; } T& operator *() { return *gp.ptr; } iterator& operator++(); }; 

Problem 2 : move to the next item.



If a thread B removes the element following the one on which the iterator is positioned - in this case 42, - the incrementing operation of the iterator will result in a call to the deleted element, that is, garbage.

This problem is more complicated than the first one, since the threads do not know that we are going around the container and are free to remove / add any elements. You can think of somehow marking the element pointed to by the iterator and analyzing such a flag when deleting an element, but this at least complicates the internal structure of the container (and as a maximum, such reasoning will not lead to anything). There is another way that an interesting data structure tells us - the multi-level array.

Multi-level array

This data structure was proposed in 2013 by Steve Feldman and is an associative container, that is, a hash map.



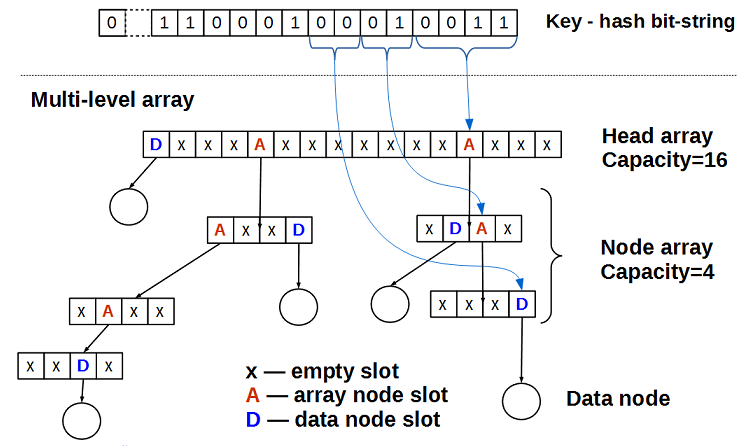
Imagine that a hash is a bit string of constant length. We will consider the bits of this string as indices in a multilevel array: the first M bits is the index in the head array head array (in the figure M = 4, that is, the size of the head array is 2 ** 4 = 16), the next portions of N bits are indices in the underlying arrays of the node array (in the figure, N = 2 and the dimension of the node array is 2 ** 2 = 4). The array element can be:

• is empty
• data pointer
• pointer to the next level array

An empty multi-level array consists only of the head array, in which all cells are empty.

Adding data data with the key key to the multi-level array occurs according to the following algorithm:

• 1. calculate the hash key h = hash( key )
• 2. Take the first M bits of the hash h - this is the index i cell in the head array
• 3a. If the cell is empty ( head_array[i] == nullptr ), then put the data in it: head_array[i].CAS( nullptr, &data ) - and exit. Since we have a lock-free container, we use atomic operations, in this case CAS (compare-and-swap, in terms of C ++ 11 is std::compare_exchange ).
• 3b. If the cell contains data ( head_array[i] = di ), you need to split it, that is, create a node array of the next level, put di in it and go to step 4.
• 3c. If the cell contains a pointer to the underlying node array - go to step 4.
• 4. The current array is a certain node array. Take the next N bits of the key hash h , these bits will be the index i in the current node array. If all the bits of the hash are exhausted, this means that there is already an element in the container with the same hash and the insertion of the data data ends in failure.
• 4a. If the cell is empty ( current_node_array[i] == nullptr ), then put the data in it: current_node_array[i].CAS( nullptr, &data ) - and exit
• 4b. If the cell contains data ( current_node_array[i] = di ), you need to split it, that is, create the next level node array, put di in it and go to step 4.
• 4c. If the cell contains a pointer to the underlying node array - go to step 4.

As you can see, the insertion algorithm is very simple and intuitive - it is easier to draw than to describe it. The deletion algorithm is even simpler: considering the hash value of the key to be deleted as a bit string, selecting bits and interpreting them as indices in arrays, we go down the links to an array whose cell is either empty or contains data. If the cell is empty, it means that our key (more precisely, its hash) is not in the container and there is nothing to delete. If the cell contains data and the key of this data is the required key, change the value of the cell to nullptr using the atomic CAS operation. Note that when deleting, we simply reset the array cell, the node_array itself will never be deleted, this fact will be useful to us in the future.

The question remains: how to distinguish what the cell of the array contains — data or a pointer to the next level array. In normal programming, we would put a boolean attribute in each slot of the array:

 struct array_slot { union { T* data; node_array* array; }; bool is_array; // ,    — data  array }; 

But our programming is unusual, and this approach will not suit us. The unusual thing is that we have to operate with the atomic primitive CAS, which has a limit on the length of the data. That is, we must be able to change the value of the cell and the is_array attribute atomically, with a single CAS.
This is not a problem if you read the previous part of the lock-free epic and know that there is such a thing as a marked pointer . We will store the is_array in the is_array bit of the array cell pointer:

 template <typename T> using array_slot = marked_ptr<T*, 3 >; 

Thus, an array cell is just a pointer, in which we use the last 2 bits ( marked_ptr mask 3) for internal flags: one bit for the “cell contains a pointer to the next level array” flag, plus one more bit for ... and for what ? ..

Let's look carefully at the insertion algorithm. Steps 3b and 4b speak of splitting a cell, that is, turning it from a cell containing data into a cell containing a pointer to the underlying array. Such a transformation is quite long, as it requires:

• create a new node_array;
• zeroing all its elements;
• finding a position in the new node_array for the split cell data;
• writing to the new node_array in the found position of the split cell data;
• and finally, setting a new split cell value

As long as all these actions are performed, the split cell is in an undefined state. This is the state we encode the second low-order bit. All operations on the multi-level array, having met the “cell splitting” flag, wait for the end of splitting of such a cell using active waiting (spinning) on ​​this flag:


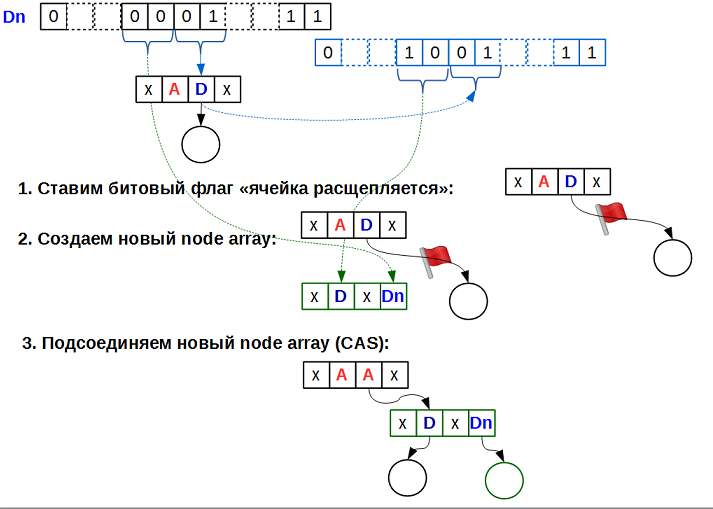
in the figure, the black data is the added key Dn , the blue ones is the existing D


The multi-level array data structure is simple and interesting, but its features (I wanted to write "flaws", but these are still features) are:

• it requires perfect hashing. The ideal hash function is such a hash function h , which for any keys k1 and k2 such that k1 != k2 , gives different hash values: h(k1)!= h(k2) . That is, the multi-level array does not allow collisions.
• keys (or key hash values) of different sizes are not supported. That is, a variable-length std::string key cannot be used as a bit string.

But if your key is of a constant size (or you have an ideal hash function), the multi-level array is a very good lock-free container, IMHO.

In principle, it is possible to generalize the multi-level array so that it supports collision lists: it’s enough to use the lock-free list as a collision list instead of data. Another generalization for keys of variable length: assume that all other bits in the bit string of a short key are zero.


But for the purposes of this article, one property of the multi-level array is important: the once-created node array is never deleted. And this implies a powerful consequence: the multi-level array supports thread-safe iterators , moreover, these are bidirectional iterators. In fact, since node arrays are not deleted, the iterator is a pointer to the node array plus an index to the node array, which is a “pointer” to the cell:

 class iterator { guarded_ptr<T> gp_; node_array* node_; int node_index_; }; 

guarded_ptr is required here, since the concurrent flow can delete data for which the iterator is positioned; guarded_ptr prevents physical removal. It turns out that the iterator can point to an element that is removed from the container - another unexpected property of the lock-free data structures. But if you think well, this property is quite explicable: in an ever-changing world that competitive containers are, only one thing can be guaranteed: at the time of iterator positioning, this cell contained valid data.
The node_ pointer to node_array and its index node_index_ necessary in the iterator to go to the next (or previous) element of the container, that is, they actually determine the current position of the iterator in the container.

It is interesting to note that if we have keys of constant size, and not hash values, then the bypass of the multi-level array is ordered.


Summarizing, we can say: there are still competitive containers that support thread-safe iterators, one of such containers is a multi-level array. Are there others? .. Is it possible to create an iterable lock-free list, which is the basis for many interesting lock-free map? ..

The answer to this question is in the next article.